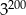Wartość wyrażenia 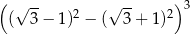 jest równa
jest równa
A) 512 B) 0 C) 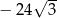 D)
D) 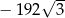
/Szkoła średnia/Zadania testowe
Wartość wyrażenia 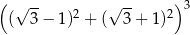 jest równa
jest równa
A) 512 B) 0 C) 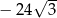 D)
D) 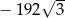
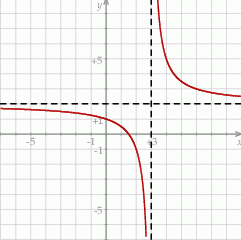
Na rysunku przedstawiono fragment wykresu funkcji homograficznej 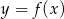 , której dziedziną jest zbiór
, której dziedziną jest zbiór 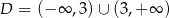 .
.
Równanie 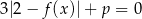 z niewiadomą
z niewiadomą  ma dokładnie dwa rozwiązania tylko wtedy, gdy
ma dokładnie dwa rozwiązania tylko wtedy, gdy
A) 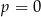 B)
B) 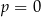 lub
lub 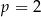 C)
C) 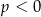 D)
D) 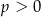
Wartość wyrażenia 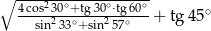 wynosi
wynosi
A) 2 B) 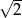 C) 3 D)
C) 3 D) 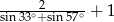
Przeciwprostokątna 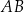 trójkąta prostokątnego
trójkąta prostokątnego  ma długość 26, a pole tego trójkąta jest równe 120 (zobacz rysunek).
ma długość 26, a pole tego trójkąta jest równe 120 (zobacz rysunek).
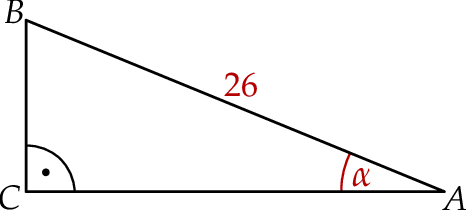
Jeżeli  jest najmniejszym z kątów wewnętrznych tego trójkąta, to wartość wyrażenia
jest najmniejszym z kątów wewnętrznych tego trójkąta, to wartość wyrażenia 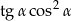 jest równa
jest równa
A) 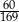 B)
B) 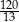 C)
C) 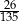 D)
D) 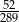
Rzucamy sześć razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania sześciu różnych liczb oczek, jest równe
A) 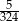 B)
B) 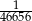 C)
C)  D)
D) 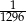
Długości boków prostokąta są równe 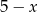 i
i 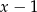 . Pole prostokąta jest największe, gdy liczba
. Pole prostokąta jest największe, gdy liczba  jest równa
jest równa
A) 2 B) 1 C) 4 D) 3
Długości boków prostokąta są równe 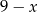 i
i 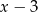 . Pole prostokąta jest największe, gdy liczba
. Pole prostokąta jest największe, gdy liczba  jest równa
jest równa
A) 7 B) 6 C) 4 D) 5
Długości boków prostokąta są równe 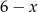 i
i 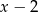 . Pole prostokąta jest największe, gdy liczba
. Pole prostokąta jest największe, gdy liczba  jest równa
jest równa
A) 2 B) 5 C) 4 D) 3
Wielomian 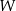 określony jest wzorem
określony jest wzorem 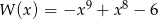 . Zatem
. Zatem 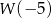 jest liczbą
jest liczbą
A) ujemną B) dodatnią C) niewymierną D) pierwszą
Wielomian 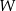 określony jest wzorem
określony jest wzorem 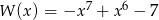 . Zatem
. Zatem 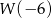 jest liczbą
jest liczbą
A) ujemną B) niewymierną C) dodatnią D) pierwszą
Wielomian 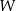 określony jest wzorem
określony jest wzorem 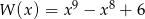 . Zatem
. Zatem 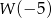 jest liczbą
jest liczbą
A) ujemną B) dodatnią C) niewymierną D) pierwszą
Znajdź skalę podobieństwa trójkąta 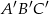 do trójkąta
do trójkąta 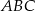 :
:
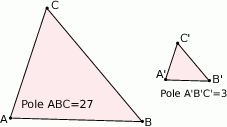
A) 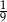 B)
B) 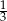 C) 3 D) 9
C) 3 D) 9
Znajdź skalę podobieństwa trójkąta 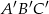 do trójkąta
do trójkąta 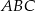 :
:
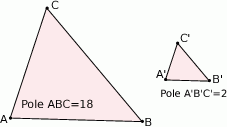
A) 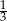 B)
B) 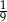 C) 3 D) 9
C) 3 D) 9
Rozwiązaniem nierówności 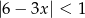 jest zbiór
jest zbiór
A) 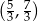 B)
B) 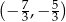 C)
C) 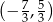 D)
D) 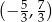
Rozwiązaniem nierówności 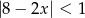 jest zbiór
jest zbiór
A) 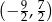 B)
B) 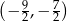 C)
C) 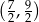 D)
D) 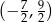
Liczba 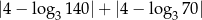 jest równa
jest równa
A) 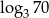 B)
B) 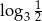 C)
C) 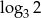 D)
D) 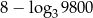
Liczb całkowitych spełniających nierówność 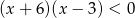 jest
jest
A) 8 B) 0 C) 7 D) nieskończenie wiele
Liczb całkowitych spełniających nierówność 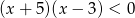 jest
jest
A) 8 B) 0 C) 7 D) 9
Liczb całkowitych spełniających nierówność 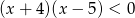 jest
jest
A) 0 B) 8 C) 7 D) 10
Dłuższy bok prostokąta ma długość 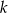 . Przekątna prostokąta tworzy z krótszym bokiem kąt
. Przekątna prostokąta tworzy z krótszym bokiem kąt  . Długość przekątnej prostokąta wynosi
. Długość przekątnej prostokąta wynosi
A) 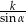 B)
B) 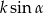 C)
C) 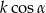 D)
D) 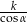
Ile jest liczb całkowitych spełniających nierówność 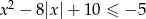 ?
?
A) 1 B) 2 C) 3 D) 6
Liczba 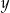 to 120% liczby
to 120% liczby  . Wynika stąd, że
. Wynika stąd, że
A) 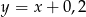 B)
B) 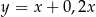 C)
C) 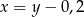 D)
D) 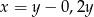
Liczba  stanowi 20% liczby
stanowi 20% liczby 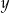 . Zatem prawdziwe jest następujące równanie
. Zatem prawdziwe jest następujące równanie
A) 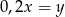 B)
B) 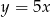 C)
C) 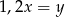 D)
D) 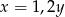
Dodatnia liczba  stanowi 30% liczby
stanowi 30% liczby 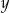 . Wówczas
. Wówczas
A) 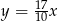 B)
B) 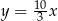 C)
C) 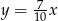 D)
D) 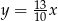
Liczba 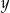 to 140% liczby
to 140% liczby  . Wynika stąd, że
. Wynika stąd, że
A) 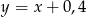 B)
B) 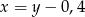 C)
C) 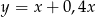 D)
D) 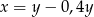
Liczba  jest o 30% większa od liczby
jest o 30% większa od liczby 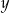 . Z tego wynika, że
. Z tego wynika, że
A) 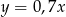 B)
B) 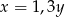 C)
C) 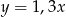 D)
D) 
Dodatnia liczba  stanowi 70% liczby
stanowi 70% liczby 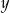 . Wówczas
. Wówczas
A) 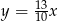 B)
B) 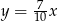 C)
C) 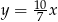 D)
D) 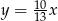
Liczba 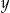 jest o 30% większa od liczby
jest o 30% większa od liczby  . Z tego wynika, że
. Z tego wynika, że
A) 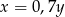 B)
B) 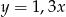 C)
C) 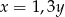 D)
D) 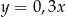
Liczba  stanowi 60% liczby
stanowi 60% liczby 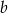 . Wówczas:
. Wówczas:
A) 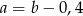 B)
B) 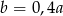 C)
C) 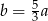 D)
D) 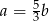
Liczba  jest o 30% mniejsza od liczby
jest o 30% mniejsza od liczby 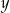 . Z tego wynika, że
. Z tego wynika, że
A) 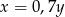 B)
B) 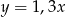 C)
C) 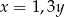 D)
D) 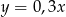
Liczba 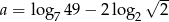 . Wynika z tego, że
. Wynika z tego, że
A) 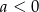 B)
B) 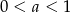 C)
C) 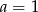 D)
D) 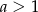
Liczba 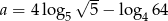 . Wynika z tego, że
. Wynika z tego, że
A) 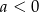 B)
B) 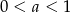 C)
C) 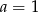 D)
D) 
Liczba 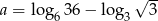 . Wynika z tego, że
. Wynika z tego, że
A) 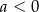 B)
B) 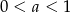 C)
C) 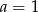 D)
D) 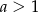
Funkcja 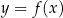 jest określona za pomocą tabeli
jest określona za pomocą tabeli
 | 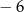 | 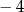 | 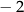 | 0 | 2 | 4 | 6 |
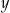 | 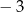 | 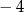 | 4 | 1 | 5 | 0 | 2 |
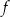 jest równe
jest równe A) 1 B) 2 C) 4 D) 5 E) 6
Po rozłożeniu wielomianu 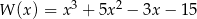 otrzymujemy
otrzymujemy
A) 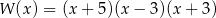 B)
B) 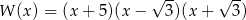
C) 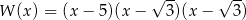 D)
D) 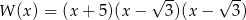
Wielomian 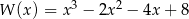 można przedstawić w postaci
można przedstawić w postaci
A) 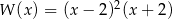 B)
B) 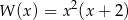
C) 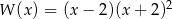 D)
D) 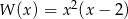
Wielomian 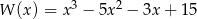 rozłożony na czynniki ma postać
rozłożony na czynniki ma postać
A) 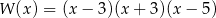 B)
B) 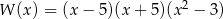
C) 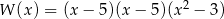 D)
D) 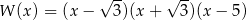
Wielomian 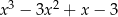 po rozłożeniu na czynniki ma postać:
po rozłożeniu na czynniki ma postać:
A) 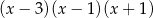 B)
B) 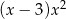
C) 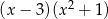 D)
D) 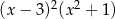
Wielomian 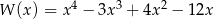 po rozłożeniu na czynniki ma postać:
po rozłożeniu na czynniki ma postać:
A) 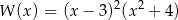 B)
B) 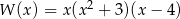
C) 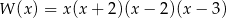 D)
D) 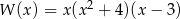
W trapezie równoramiennym kąt ostry ma miarę 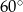 , a podstawy mają długości 12 i 6. Wysokość tego trapezu jest równa
, a podstawy mają długości 12 i 6. Wysokość tego trapezu jest równa
A) 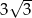 B)
B) 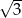 C)
C)  D)
D) 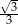
Dany jest ciąg arytmetyczny 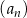 , określony dla
, określony dla 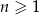 , o którym wiemy, że:
, o którym wiemy, że: 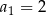 i
i 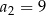 . Wtedy
. Wtedy 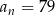 dla
dla
A) 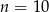 B)
B) 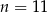 C)
C) 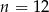 D)
D) 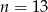
Dany jest ciąg arytmetyczny 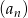 , określony dla
, określony dla 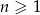 , o którym wiemy, że:
, o którym wiemy, że: 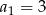 i
i 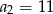 . Wtedy
. Wtedy 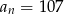 dla
dla
A) 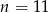 B)
B) 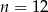 C)
C) 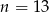 D)
D) 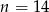
W ciągu arytmetycznym 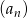 , określonym dla
, określonym dla 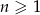 , dane są:
, dane są: 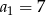 ,
, 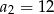 . Wtedy
. Wtedy
A) 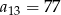 B)
B) 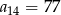 C)
C) 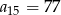 D)
D) 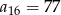
W ciągu arytmetycznym 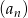 , określonym dla
, określonym dla 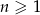 , dane są:
, dane są: 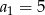 ,
, 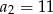 . Wtedy
. Wtedy
A) 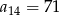 B)
B) 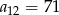 C)
C) 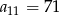 D)
D) 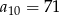
Liczba 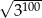 jest równa
jest równa
A) 320 B) 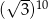 C)
C) 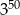 D)
D)