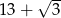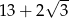Punkt 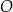 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 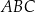 oraz
oraz 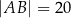 ,
, 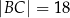 . Prosta
. Prosta 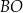 przecina bok
przecina bok 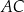 trójkąta
trójkąta 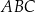 w punkcie
w punkcie 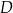 (zobacz rysunek).
(zobacz rysunek).

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Proste 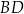 i i 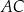 są prostopadłe. są prostopadłe. | P | F |
Stosunek pól trójkątów 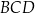 i i 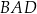 jest równy 0,9. jest równy 0,9. | P | F |

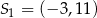 oraz okrąg o środku
oraz okrąg o środku 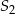 i promieniu 6 są styczne wewnętrznie w punkcie
i promieniu 6 są styczne wewnętrznie w punkcie 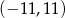 . Wtedy
. Wtedy 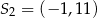
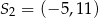
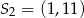
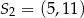
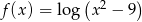 nie należy liczba
nie należy liczba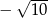
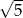
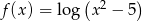 nie należy liczba
nie należy liczba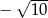
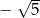
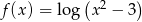 nie należy liczba
nie należy liczba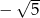
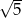
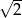
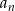 dany jest wzorem
dany jest wzorem 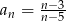 , gdzie
, gdzie 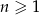 oraz
oraz 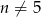 . Liczba wyrazów całkowitych tego ciągu to
. Liczba wyrazów całkowitych tego ciągu to 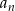 dany jest wzorem
dany jest wzorem 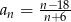 , gdzie
, gdzie 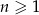 . Liczba wyrazów całkowitych tego ciągu to
. Liczba wyrazów całkowitych tego ciągu to 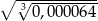 jest równa
jest równa 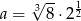 i
i 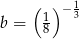 , to wartość wyrażenia
, to wartość wyrażenia 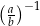 jest równa
jest równa 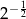
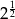
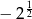
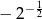
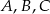 i
i 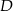 leżą na okręgu o środku
leżą na okręgu o środku 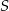 . Cięciwa
. Cięciwa 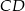 przecina średnicę
przecina średnicę 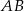 tego okręgu w punkcie
tego okręgu w punkcie 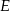 tak, że
tak, że 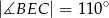 . Kąt środkowy
. Kąt środkowy 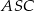 ma miarę
ma miarę 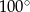 (zobacz rysunek).
(zobacz rysunek). 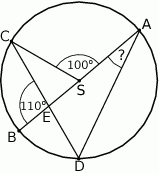
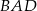 ma miarę
ma miarę 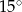
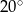
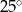
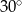
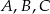 i
i 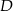 leżą na okręgu o środku
leżą na okręgu o środku 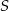 . Cięciwa
. Cięciwa 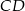 przecina średnicę
przecina średnicę 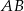 tego okręgu w punkcie
tego okręgu w punkcie 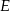 tak, że
tak, że 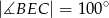 . Kąt środkowy
. Kąt środkowy 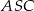 ma miarę
ma miarę 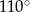 (zobacz rysunek).
(zobacz rysunek). 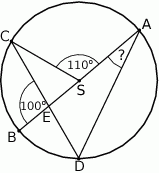
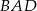 ma miarę
ma miarę 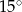
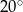
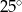
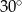
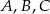 i
i 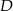 leżą na okręgu o środku
leżą na okręgu o środku 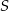 . Cięciwa
. Cięciwa 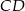 przecina średnicę
przecina średnicę 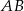 tego okręgu w punkcie
tego okręgu w punkcie 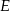 tak, że
tak, że 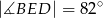 . Kąt środkowy
. Kąt środkowy 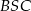 ma miarę
ma miarę 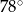 (zobacz rysunek).
(zobacz rysunek). 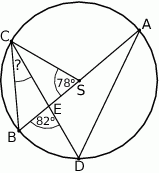
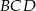 ma miarę
ma miarę 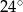
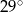
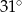
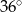
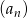 mamy:
mamy: 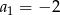 i
i 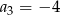 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy 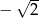
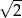
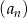 mamy:
mamy: 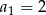 i
i 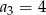 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy 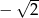
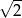
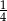 , a piąty
, a piąty 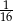 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy 
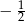
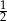
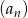 mamy:
mamy: 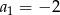 i
i 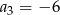 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy 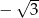
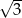
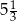 , a siódmy
, a siódmy 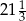 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy 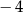
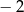
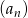 mamy:
mamy: 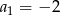 i
i 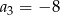 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy 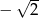
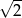
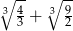 jest równa
jest równa 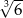
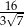
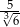
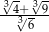
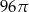
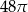
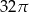
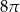
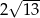 . Objętość tego stożka jest równa
. Objętość tego stożka jest równa 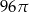
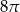
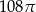
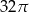
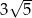 . Objętość tego stożka jest równa
. Objętość tego stożka jest równa 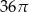
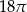
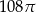
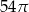
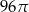
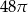
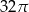
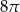
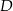 i
i 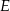 leżą na okręgu opisanym na trójkącie równobocznym
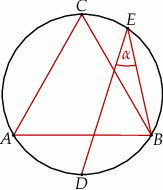
leżą na okręgu opisanym na trójkącie równobocznym 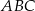 (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek 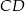 jest średnicą tego okręgu. Kąt wpisany
jest średnicą tego okręgu. Kąt wpisany 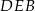 ma miarę
ma miarę  .
. 
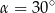
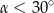
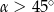
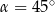
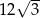 . Bok tego sześciokąta ma długość
. Bok tego sześciokąta ma długość 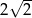
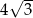
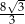 . Obwód tego sześciokąta jest równy
. Obwód tego sześciokąta jest równy 
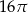 (mniejszy okrąg jest styczny do boków kwadratu
(mniejszy okrąg jest styczny do boków kwadratu 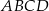 , a do większego okręgu należą punkty
, a do większego okręgu należą punkty 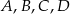 ). Zatem długość boku kwadratu
). Zatem długość boku kwadratu 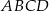 jest równa:
jest równa: 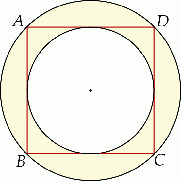
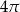 (mniejszy okrąg jest wpisany w trójkąt
(mniejszy okrąg jest wpisany w trójkąt 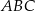 , a wierzchołki
, a wierzchołki 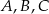 leżą na większym okręgu). Zatem długość boku trójkąta równobocznego
leżą na większym okręgu). Zatem długość boku trójkąta równobocznego 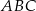 jest równa:
jest równa: 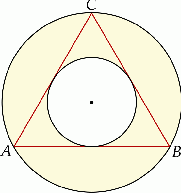
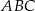 bok
bok 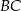 ma długość 13, a wysokość
ma długość 13, a wysokość 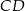 tego trójkąta dzieli bok
tego trójkąta dzieli bok 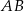 na odcinki o długościach
na odcinki o długościach 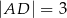 i
i 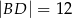 (zobacz rysunek obok).
(zobacz rysunek obok). 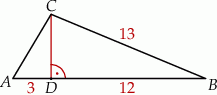
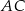 jest równa
jest równa 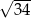
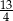
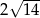
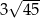
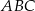 bok
bok 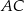 ma długość 10, a wysokość
ma długość 10, a wysokość 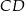 tego trójkąta dzieli bok
tego trójkąta dzieli bok 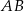 na odcinki o długościach
na odcinki o długościach 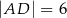 i
i 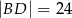 (zobacz rysunek obok).
(zobacz rysunek obok). 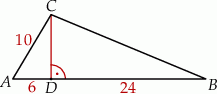
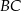 jest równa
jest równa 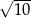
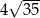
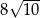
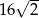
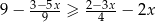 jest taki sam jak zbiór rozwiązań nierówności
jest taki sam jak zbiór rozwiązań nierówności 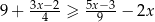
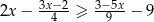
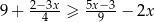
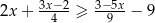
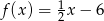
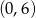
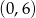
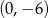
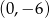
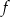 określona jest wzorem
określona jest wzorem 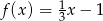 dla wszystkich liczb rzeczywistych
dla wszystkich liczb rzeczywistych  . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe.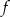 jest malejąca i jej wykres przecina oś
jest malejąca i jej wykres przecina oś 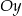 w punkcie
w punkcie 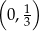
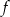 jest malejąca i jej wykres przecina oś
jest malejąca i jej wykres przecina oś 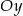 w punkcie
w punkcie 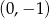
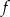 jest rosnąca i jej wykres przecina oś
jest rosnąca i jej wykres przecina oś 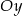 w punkcie
w punkcie 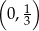
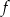 jest rosnąca i jej wykres przecina oś
jest rosnąca i jej wykres przecina oś 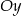 w punkcie
w punkcie 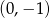
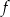 określona jest wzorem
określona jest wzorem 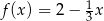 dla wszystkich liczb rzeczywistych
dla wszystkich liczb rzeczywistych  . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe.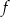 jest malejąca i jej wykres przecina oś
jest malejąca i jej wykres przecina oś 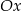 w punkcie
w punkcie 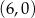
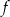 jest malejąca i jej wykres przecina oś
jest malejąca i jej wykres przecina oś 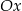 w punkcie
w punkcie 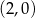
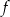 jest rosnąca i jej wykres przecina oś
jest rosnąca i jej wykres przecina oś 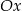 w punkcie
w punkcie 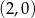
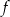 jest rosnąca i jej wykres przecina oś
jest rosnąca i jej wykres przecina oś 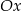 w punkcie
w punkcie 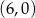
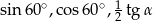 w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Kąt
w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Kąt  jest kątem ostrym. Zatem jego miara jest równa
jest kątem ostrym. Zatem jego miara jest równa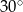
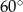
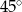
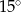
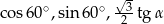 w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Kąt
w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Kąt  jest kątem ostrym. Zatem jego miara jest równa
jest kątem ostrym. Zatem jego miara jest równa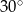
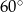
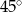
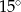
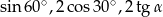 w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Kąt
w podanej kolejności są trzema kolejnymi wyrazami ciągu geometrycznego. Kąt  jest kątem ostrym. Zatem jego miara jest równa
jest kątem ostrym. Zatem jego miara jest równa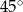
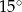
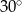
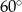
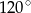 . Obwód trapezu jest równy
. Obwód trapezu jest równy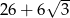
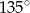 . Obwód trapezu jest równy
. Obwód trapezu jest równy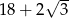
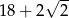
 . Obwód trapezu jest równy
. Obwód trapezu jest równy