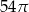Obwód prostokąta jest równy 32 cm, a jeden z jego boków jest 3 razy dłuższy od drugiego boku. Pole tego prostokąta jest równe:
A) 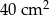 B)
B) 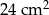 C)
C) 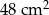 D)
D) 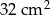
/Szkoła średnia/Zadania testowe
Obwód prostokąta jest równy 36 cm, a jeden z jego boków jest 5 razy dłuższy od drugiego boku. Pole tego prostokąta jest równe:
A) 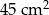 B)
B) 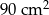 C)
C) 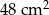 D)
D) 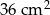
Liczba pierwiastków wielomianu 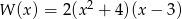 jest równa
jest równa
A) 4 B) 3 C) 2 D) 1
Liczba pierwiastków rzeczywistych wielomianu 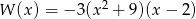 jest równa
jest równa
A) 1 B) 2 C) 3 D) 4
Liczba rozwiązań równania 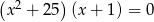 to
to
A) 3 B) 2 C) 1 D) 0
Zosia czyta  stron książki w ciągu
stron książki w ciągu 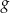 godzin. Wynika stąd, że w ciągu
godzin. Wynika stąd, że w ciągu 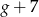 godzin przeczyta stron
godzin przeczyta stron
A) 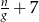 B)
B) 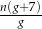 C)
C) 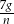 D)
D) 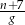
Kasia czyta  stron książki w ciągu
stron książki w ciągu 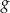 godzin. Wynika stąd, że w ciągu
godzin. Wynika stąd, że w ciągu 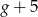 godzin przeczyta stron
godzin przeczyta stron
A) 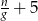 B)
B) 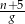 C)
C) 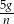 D)
D) 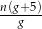
Jacek czyta średnio 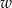 wyrazów w ciągu
wyrazów w ciągu 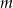 minut. Wynika stąd, że w ciągu
minut. Wynika stąd, że w ciągu 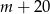 minut przeczyta wyrazów
minut przeczyta wyrazów
A) 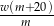 B)
B) 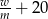 C)
C) 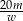 D)
D) 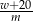
Wyrażenie 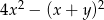 po rozłożeniu na czynniki przyjmuje postać:
po rozłożeniu na czynniki przyjmuje postać:
A) 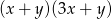 B)
B) 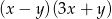 C)
C) 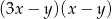 D)
D) 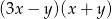
Wyrażenie 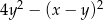 jest równe wyrażeniu:
jest równe wyrażeniu:
A) 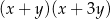 B)
B) 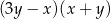 C)
C) 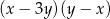 D)
D) 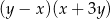
Wyrażenie 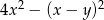 po rozłożeniu na czynniki przyjmuje postać:
po rozłożeniu na czynniki przyjmuje postać:
A) 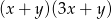 B)
B) 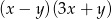 C)
C) 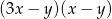 D)
D) 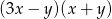
Liczba 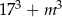 jest podzielna przez 19 dla
jest podzielna przez 19 dla
A) 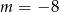 B)
B) 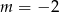 C)
C) 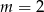 D)
D) 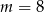
Zbiór rozwiązań równania 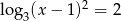 jest taki sam, jak zbiór rozwiązań równania:
jest taki sam, jak zbiór rozwiązań równania:
A) 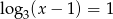 B)
B) 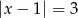 C)
C) 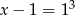 D)
D) 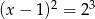
Zbiór rozwiązań równania 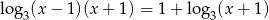 jest taki sam, jak zbiór rozwiązań równania:
jest taki sam, jak zbiór rozwiązań równania:
A) 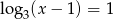 B)
B) 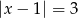 C)
C) 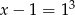 D)
D) 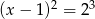
Cięciwy 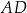 i
i 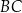 okręgu o środku
okręgu o środku 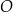 przecinają się w punkcie
przecinają się w punkcie 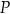 tak, że
tak, że 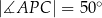 (zobacz rysunek).
(zobacz rysunek).

Jeżeli punkt 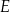 jest punktem wspólnym prostych
jest punktem wspólnym prostych 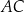 i
i 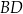 , to miara kąta
, to miara kąta 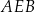 jest równa
jest równa
A) 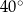 B)
B) 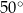 C)
C) 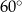 D)
D) 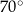
Przekrojem osiowym stożka jest trójkąt równoboczny o boku długości 6. Objętość tego stożka jest równa
A) 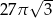 B)
B) 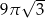 C)
C) 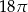 D)
D) 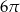
Przekrojem osiowym stożka jest trójkąt równoboczny o boku długości 4. Objętość tego stożka jest równa
A) 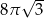 B)
B) 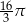 C)
C) 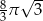 D)
D) 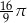
Iloczyn wielomianów 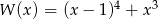 i
i 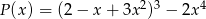 jest wielomianem stopnia
jest wielomianem stopnia
A) 24 B) 10 C) 12 D) 7
Punkt 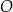 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 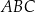 oraz
oraz 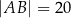 ,
, 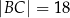 . Prosta
. Prosta 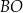 przecina bok
przecina bok 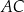 trójkąta
trójkąta 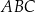 w punkcie
w punkcie 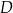 (zobacz rysunek).
(zobacz rysunek).

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Proste 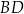 i i 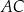 są prostopadłe. są prostopadłe. | P | F |
Stosunek pól trójkątów 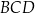 i i 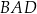 jest równy 0,9. jest równy 0,9. | P | F |
Okrąg o środku 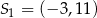 oraz okrąg o środku
oraz okrąg o środku 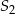 i promieniu 6 są styczne wewnętrznie w punkcie
i promieniu 6 są styczne wewnętrznie w punkcie 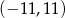 . Wtedy
. Wtedy
A) 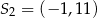 B)
B) 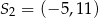 C)
C) 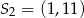 D)
D) 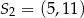
Do dziedziny funkcji 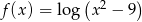 nie należy liczba
nie należy liczba
A) -5 B) 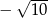 C)
C) 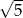 D) 6
D) 6
Do dziedziny funkcji 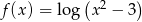 nie należy liczba
nie należy liczba
A) -5 B) 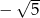 C)
C) 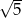 D)
D) 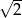
Do dziedziny funkcji 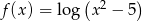 nie należy liczba
nie należy liczba
A) 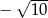 B)
B) 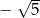 C) -5 D) 6
C) -5 D) 6
Ciąg 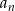 dany jest wzorem
dany jest wzorem 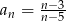 , gdzie
, gdzie 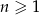 oraz
oraz 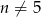 . Liczba wyrazów całkowitych tego ciągu to
. Liczba wyrazów całkowitych tego ciągu to
A) 1 B) 2 C) 3 D) 4
Ciąg 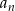 dany jest wzorem
dany jest wzorem 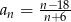 , gdzie
, gdzie 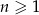 . Liczba wyrazów całkowitych tego ciągu to
. Liczba wyrazów całkowitych tego ciągu to
A) 2 B) 3 C) 4 D) 6
Liczba 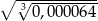 jest równa
jest równa
A) 0,02 B) 0,2 C) 0,04 D) 0,08
Jeżeli 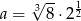 i
i 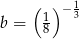 , to wartość wyrażenia
, to wartość wyrażenia 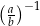 jest równa
jest równa
A) 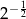 B)
B) 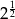 C)
C) 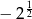 D)
D) 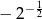
Punkty 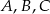 i
i 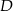 leżą na okręgu o środku
leżą na okręgu o środku 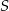 . Cięciwa
. Cięciwa 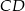 przecina średnicę
przecina średnicę 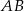 tego okręgu w punkcie
tego okręgu w punkcie 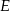 tak, że
tak, że 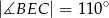 . Kąt środkowy
. Kąt środkowy 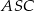 ma miarę
ma miarę 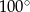 (zobacz rysunek).
(zobacz rysunek).
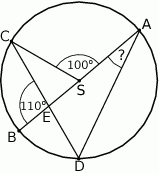
Kąt wpisany 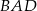 ma miarę
ma miarę
A) 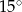 B)
B) 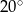 C)
C) 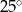 D)
D) 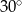
Punkty 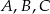 i
i 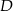 leżą na okręgu o środku
leżą na okręgu o środku 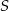 . Cięciwa
. Cięciwa 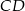 przecina średnicę
przecina średnicę 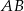 tego okręgu w punkcie
tego okręgu w punkcie 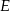 tak, że
tak, że 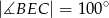 . Kąt środkowy
. Kąt środkowy 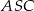 ma miarę
ma miarę 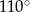 (zobacz rysunek).
(zobacz rysunek).
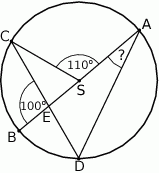
Kąt wpisany 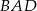 ma miarę
ma miarę
A) 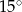 B)
B) 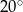 C)
C) 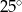 D)
D) 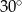
Punkty 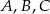 i
i 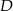 leżą na okręgu o środku
leżą na okręgu o środku 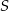 . Cięciwa
. Cięciwa 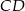 przecina średnicę
przecina średnicę 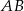 tego okręgu w punkcie
tego okręgu w punkcie 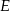 tak, że
tak, że 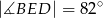 . Kąt środkowy
. Kąt środkowy 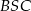 ma miarę
ma miarę 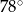 (zobacz rysunek).
(zobacz rysunek).
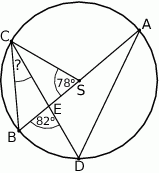
Kąt wpisany 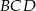 ma miarę
ma miarę
A) 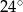 B)
B) 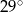 C)
C) 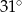 D)
D) 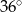
W malejącym ciągu geometrycznym 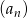 mamy:
mamy: 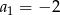 i
i 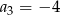 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) -2 B) 2 C) 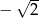 D)
D) 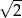
Piąty wyraz rosnącego ciągu geometrycznego jest równy 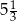 , a siódmy
, a siódmy 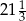 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 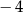 B) 2 C)
B) 2 C) 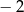 D) 4
D) 4
Trzeci wyraz malejącego ciągu geometrycznego jest równy 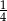 , a piąty
, a piąty 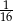 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A)  B)
B) 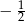 C)
C) 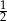 D) 2
D) 2
W malejącym ciągu geometrycznym 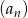 mamy:
mamy: 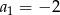 i
i 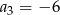 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 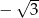 B)
B) 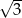 C) -3 D) 3
C) -3 D) 3
W malejącym ciągu geometrycznym 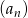 mamy:
mamy: 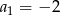 i
i 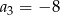 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) -2 B) 2 C) 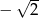 D)
D) 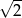
W rosnącym ciągu geometrycznym 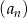 mamy:
mamy: 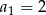 i
i 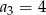 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) -2 B) 2 C) 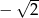 D)
D) 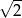
Liczba 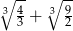 jest równa
jest równa
A) 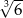 B)
B) 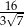 C)
C) 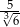 D)
D) 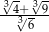
W prostopadłościanie o objętości 3400 skrócono o 10% najkrótsze krawędzie, a następnie wydłużono najdłuższe krawędzie tak, aby otrzymany prostopadłościan miał objętość 3519. O ile procent wydłużono najdłuższe krawędzie prostopadłościanu?
A) 18% B) 12% C) 15% D) 20%
Trójkąt prostokątny o przyprostokątnych 4 i 6 obracamy wokół dłuższej przyprostokątnej. Objętość powstałego stożka jest równa:
A) 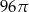 B)
B) 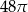 C)
C) 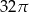 D)
D) 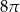
Dany jest stożek o wysokości 6 i tworzącej 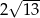 . Objętość tego stożka jest równa
. Objętość tego stożka jest równa
A) 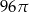 B)
B) 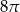 C)
C) 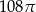 D)
D) 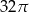
Trójkąt prostokątny o przyprostokątnych 4 i 6 obracamy wokół krótszej przyprostokątnej. Objętość powstałego stożka jest równa:
A) 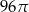 B)
B) 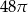 C)
C) 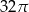 D)
D) 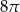
Dany jest stożek o wysokości 6 i tworzącej 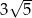 . Objętość tego stożka jest równa
. Objętość tego stożka jest równa
A) 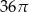 B)
B) 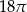 C)
C) 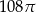 D)
D)