Ile liczb pierwszych spełnia nierówność 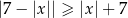 ?
?
A) 0 B) 1 C) 2 D) nieskończenie wiele
/Szkoła średnia/Zadania testowe
Rozwiązaniem równania 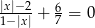 są liczby
są liczby
A) 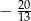 i
i 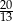 B)
B) 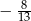 i
i 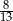 C) -8 i 8 D) -20 i 20
C) -8 i 8 D) -20 i 20
Okrąg o równaniu 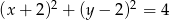 ma dwa punkty wspólne z prostą o równaniu
ma dwa punkty wspólne z prostą o równaniu
A) 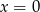 B)
B) 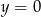 C)
C) 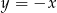 D)
D) 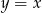
Okrąg o równaniu 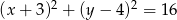 ma dwa punkty wspólne z prostą o równaniu
ma dwa punkty wspólne z prostą o równaniu
A) 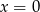 B)
B) 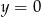 C)
C) 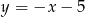 D)
D) 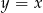
Dany jest trójkąt 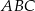 , w którym
, w którym 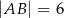 ,
, 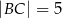 ,
, 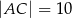 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Cosinus kąta 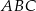 jest równy jest równy 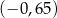 . . | P | F |
Trójkąt 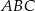 jest rozwartokątny. jest rozwartokątny. | P | F |
Dany jest trójkąt 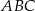 , w którym
, w którym 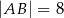 ,
, 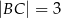 ,
, 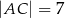 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Cosinus kąta 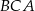 jest równy jest równy 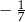 . . | P | F |
Trójkąt 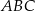 jest ostrokątny. jest ostrokątny. | P | F |
Ciąg 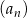 określony jest wzorem
określony jest wzorem 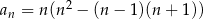 , gdzie
, gdzie 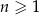 . Suma piętnastu początkowych wyrazów tego ciągu jest równa
. Suma piętnastu początkowych wyrazów tego ciągu jest równa
A) 240 B) 105 C) 120 D) 136
Liczba 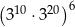 jest równa
jest równa
A) 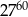 B)
B) 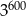 C)
C) 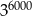 D)
D) 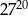
Liczba 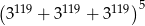 jest równa
jest równa
A) 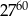 B)
B)  C)
C) 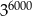 D)
D) 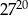
Funkcja kwadratowa 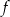 jest określona wzorem
jest określona wzorem 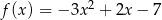 . Wykresem funkcji
. Wykresem funkcji 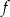 jest parabola, której wierzchołek leży na prostej o równaniu
jest parabola, której wierzchołek leży na prostej o równaniu
A) 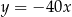 B)
B) 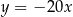 C)
C) 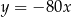 D)
D) 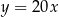
Dla każdej liczby dodatniej 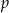 wyrażenie
wyrażenie 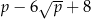 jest równe
jest równe
A) 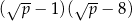 B)
B) 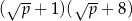
C) 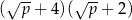 D)
D) 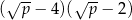
Wierzchołki trójkąta 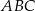 leżą na okręgu i środek
leżą na okręgu i środek 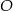 okręgu leży wewnątrz trójkąta. Jeśli kąt
okręgu leży wewnątrz trójkąta. Jeśli kąt 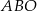 ma miarę
ma miarę 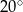 , to kąt
, to kąt 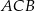 ma miarę
ma miarę
A) 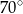 B)
B) 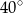 C)
C) 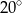 D)
D) 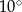
Wierzchołki trójkąta 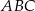 leżą na okręgu i środek
leżą na okręgu i środek 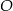 okręgu leży wewnątrz trójkąta. Jeśli kąt
okręgu leży wewnątrz trójkąta. Jeśli kąt 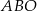 ma miarę
ma miarę 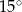 , to kąt
, to kąt 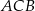 ma miarę
ma miarę
A) 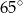 B)
B) 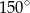 C)
C) 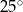 D)
D) 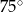
Na trójkącie ostrokątnym 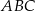 opisano okrąg o środku
opisano okrąg o środku 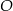 . Miara kąta
. Miara kąta 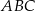 jest równa
jest równa 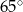 . Miara kąta
. Miara kąta 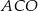 jest równa
jest równa
A) 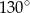 B)
B) 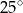 C)
C) 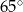 D)
D) 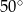
Wierzchołki trójkąta 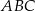 leżą na okręgu i środek
leżą na okręgu i środek 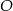 okręgu leży wewnątrz trójkąta. Jeśli kąt
okręgu leży wewnątrz trójkąta. Jeśli kąt 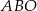 ma miarę
ma miarę 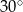 , to kąt
, to kąt 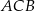 ma miarę
ma miarę
A) 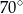 B)
B) 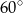 C)
C) 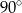 D)
D) 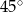
Najmniejszą wartość w przedziale 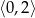 funkcja kwadratowa
funkcja kwadratowa 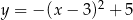 przyjmuje dla argumentu
przyjmuje dla argumentu
A) 2 B) 0 C) 3 D) 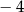
Najmniejszą wartością funkcji 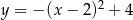 w przedziale
w przedziale 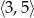 jest
jest
A) 4 B) 3 C) 0 D) 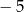
Największą wartością funkcji 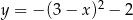 w przedziale
w przedziale 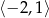 jest
jest
A) 2 B) 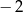 C)
C) 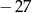 D)
D) 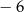
Największą wartością funkcji 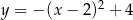 w przedziale
w przedziale 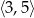 jest
jest
A) 4 B) 3 C) 0 D) 5
Najmniejszą wartość w przedziale 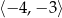 funkcja kwadratowa
funkcja kwadratowa 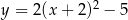 przyjmuje dla argumentu
przyjmuje dla argumentu
A) 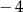 B)
B) 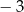 C)
C) 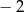 D)
D) 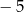
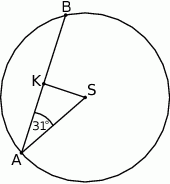
W okręgu o środku w punkcie 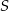 poprowadzono cięciwę
poprowadzono cięciwę 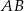 , która utworzyła z promieniem
, która utworzyła z promieniem 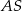 kąt o mierze
kąt o mierze 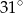 (zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu
(zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu 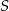 od cięciwy
od cięciwy 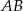 jest liczbą z przedziału
jest liczbą z przedziału
A) 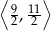 B)
B) 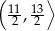 C)
C) 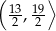 D)
D) 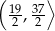
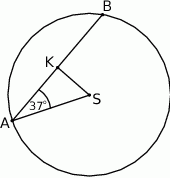
W okręgu o środku w punkcie 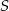 poprowadzono cięciwę
poprowadzono cięciwę 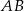 , która utworzyła z promieniem
, która utworzyła z promieniem 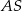 kąt o mierze
kąt o mierze 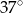 (zobacz rysunek). Promień tego okręgu ma długość 10. Długość cięciwy
(zobacz rysunek). Promień tego okręgu ma długość 10. Długość cięciwy 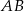 jest liczbą z przedziału
jest liczbą z przedziału
A) 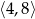 B)
B) 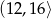 C)
C) 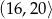 D)
D) 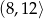
W okręgu o środku w punkcie 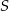 poprowadzono cięciwę
poprowadzono cięciwę 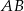 , która utworzyła z promieniem
, która utworzyła z promieniem 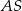 kąt o mierze
kąt o mierze 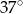 (zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu
(zobacz rysunek). Promień tego okręgu ma długość 10. Odległość punktu 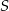 od cięciwy
od cięciwy 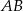 jest liczbą z przedziału
jest liczbą z przedziału
A) 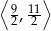 B)
B) 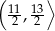 C)
C) 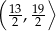 D)
D) 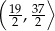
Przedstaw wyrażenie 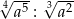 w postaci jednej potęgi
w postaci jednej potęgi
A) 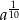 B)
B) 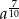 C)
C) 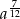 D)
D) 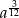
Dla każdej dodatniej liczby 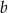 wyrażenie
wyrażenie 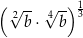 jest równe
jest równe
A) 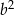 B)
B) 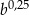 C)
C) 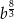 D)
D) 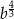
Dla każdej dodatniej liczby rzeczywistej  iloczyn
iloczyn 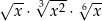 jest równy
jest równy
A) 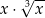 B)
B) 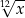 C)
C) 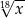 D)
D) 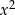
Dla każdej dodatniej liczby rzeczywistej  iloczyn
iloczyn 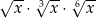 jest równy
jest równy
A)  B)
B) 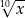 C)
C) 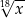 D)
D) 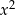
Dla każdej dodatniej liczby 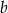 wyrażenie
wyrażenie 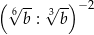 jest równe
jest równe
A) 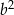 B)
B) 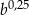 C)
C) 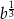 D)
D) 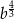
Trzecia część liczby 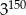 jest równa
jest równa
A) 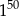 B)
B) 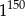 C)
C) 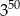 D)
D) 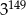
Połowa liczby 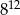 wynosi
wynosi
A) 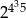 B)
B) 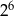 C)
C) 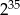 D)
D) 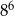
Połowa liczby 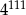 to
to
A) 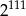 B)
B) 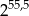 C)
C) 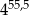 D)
D) 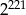
Szósta część liczby 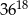 wynosi
wynosi
A) 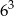 B)
B) 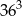 C)
C) 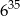 D)
D) 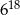
Połową liczby 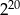 jest
jest
A) 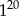 B)
B) 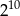 C)
C) 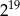 D)
D) 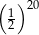
Trzecia część liczby 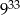 wynosi
wynosi
A) 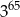 B)
B) 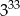 C)
C) 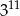 D)
D) 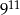
Trzecia część liczby 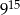 wynosi
wynosi
A) 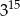 B)
B) 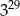 C)
C) 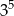 D)
D) 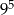
Połowa liczby 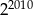 to
to
A) 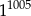 B)
B) 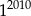 C)
C) 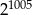 D)
D) 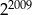
Liczba 9 razy mniejsza od 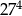 jest równa
jest równa
A) 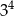 B)
B) 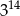 C)
C) 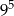 D)
D) 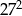
Liczba 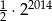 jest równa
jest równa
A) 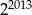 B)
B) 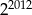 C)
C) 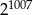 D)
D) 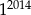
Trzecia część liczby 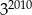 to
to
A) 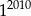 B)
B) 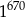 C)
C) 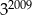 D)
D) 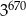
Na rysunkach poniżej znajdują się wykresy dwóch funkcji: 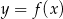 oraz
oraz 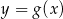 .
.
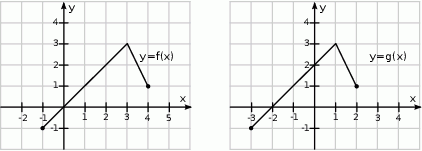
Zatem:
A) 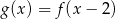 B)
B) 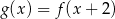
C) 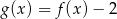 D)
D) 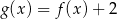
Na rysunku 1 przedstawiony jest wykres funkcji 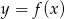 określonej dla
określonej dla 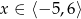 .
.
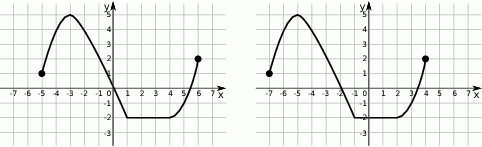
Rysunek 2 przedstawia wykres funkcji
A) 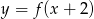 B)
B) 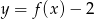 C)
C) 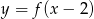 D)
D) 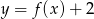
Na rysunku, w układzie współrzędnych 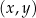 , przedstawiono wykres funkcji
, przedstawiono wykres funkcji 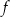 .
.
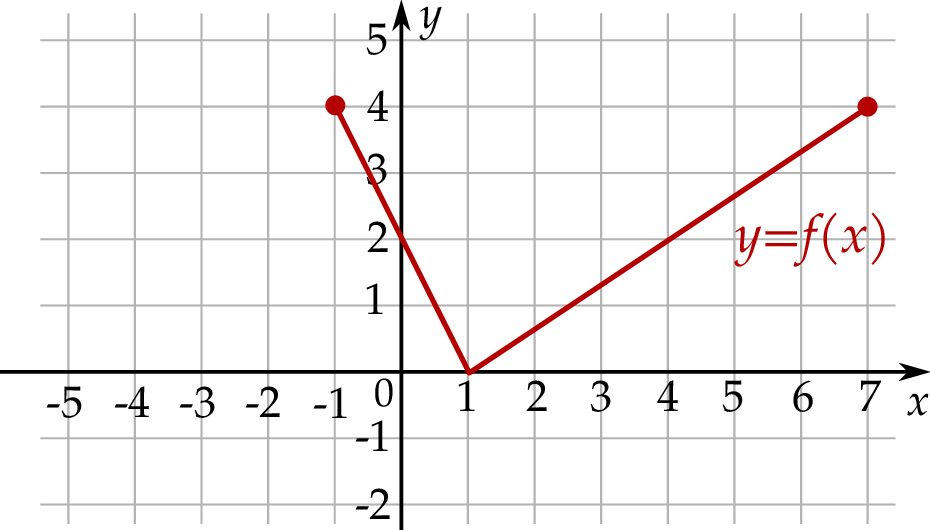
Na drugim rysunku przedstawiono wykres funkcji
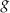 , powstałej w wyniku przesunięcia równoległego wykresu funkcji
, powstałej w wyniku przesunięcia równoległego wykresu funkcji 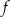 wzdłuż osi
wzdłuż osi 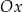 o 4 jednostki w lewo.
o 4 jednostki w lewo. 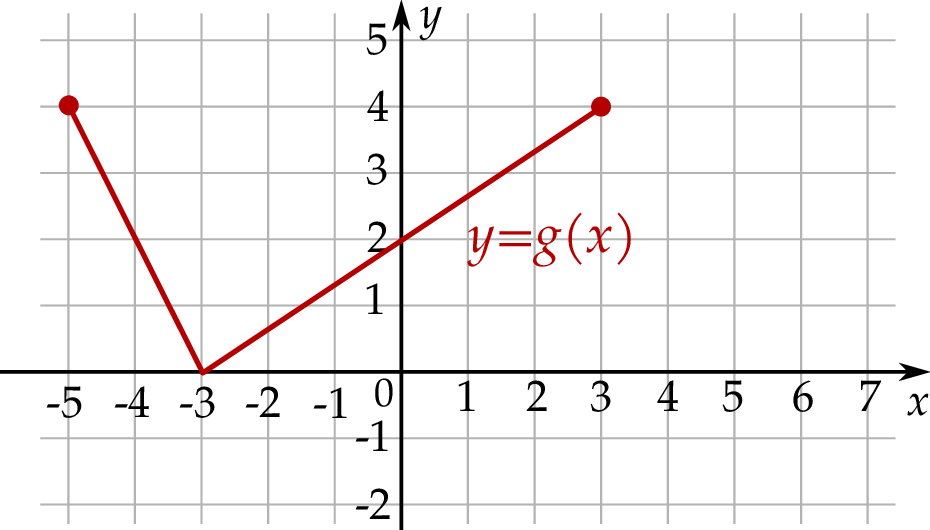
Funkcje 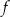 i
i 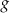 są powiązane zależnością
są powiązane zależnością
A) 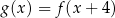 B)
B) 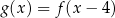
C) 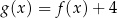 D)
D) 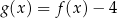
Na rysunku 1. przedstawiono wykres funkcji 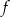 określonej na zbiorze
określonej na zbiorze 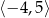 . Funkcję
. Funkcję 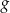 określono za pomocą funkcji
określono za pomocą funkcji 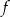 . Wykres funkcji
. Wykres funkcji 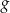 przedstawiono na rysunku 2.
przedstawiono na rysunku 2.
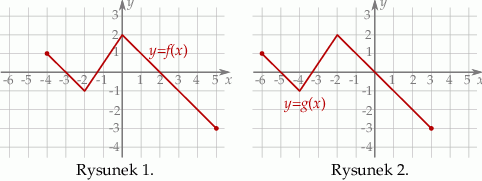
Wynika stąd, że
A) 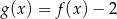 B)
B) 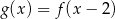
C) 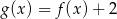 D)
D) 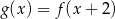
Na rysunku 1 przedstawiony jest wykres funkcji 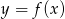 określonej dla
określonej dla 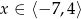 .
.
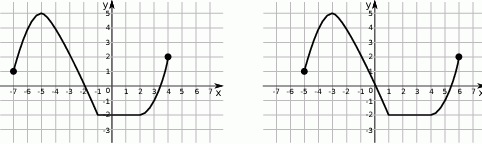
Rysunek 2 przedstawia wykres funkcji
A) 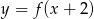 B)
B) 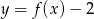 C)
C) 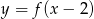 D)
D) 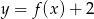
Liczba 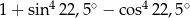 jest równa
jest równa
A) 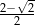 B) 1 C)
B) 1 C) 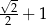 D) 2
D) 2
Zbiorem rozwiązań nierówności 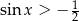 dla
dla 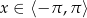 jest
jest
A) 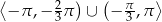 B)
B) 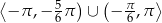
C) 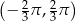 D)
D) 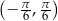
Dziedziną funkcji 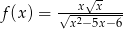 jest
jest
A) 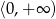 B)
B) 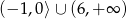 C)
C) 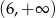 D)
D) 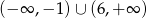
Dziedziną funkcji 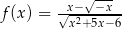 jest
jest
A) 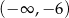 B)
B) 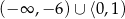 C)
C) 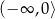 D)
D) 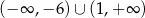
Kod, który zapisany jest na karcie dostępu, składa się z czterech cyfr. Chcemy, aby prawdopodobieństwo odkrycia tego kodu zmniejszyło się stukrotnie. Ile jeszcze cyfr należy dopisać do kodu?
A) 1 B) 2 C) 100 D) 6
Kod, który zapisany jest na karcie dostępu, składa się z czterech cyfr. Chcemy, aby prawdopodobieństwo odkrycia tego kodu zmniejszyło się tysiąckrotnie. Ile jeszcze cyfr należy dopisać do kodu?
A) 3 B) 2 C) 1000 D) 7
Kod dostępu do sejfu składa się z pięciu cyfr. Chcemy, aby prawdopodobieństwo odkrycia tego kodu zmniejszyło się stukrotnie. Ile cyfr powinien mieć nowy kod?
A) 7 B) 2 C) 100 D) 6
Do zbioru rozwiązań nierówności 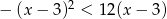 należy liczba
należy liczba
A) 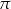 B)
B) 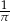 C)
C) 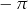 D)
D) 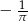
Do zbioru rozwiązań nierówności 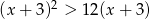 należy liczba
należy liczba
A) 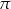 B)
B) 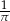 C)
C) 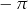 D)
D) 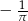
Do zbioru rozwiązań nierówności 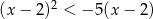 należy liczba
należy liczba
A) 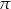 B)
B) 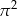 C)
C) 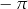 D)
D) 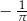
Dwa krótsze boki trójkąta rozwartokątnego 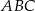 mają długości
mają długości 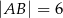 i
i 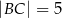 . Sinus największego kąta tego trójkąta jest równy
. Sinus największego kąta tego trójkąta jest równy  . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta 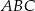 jest mniejsze od 10. jest mniejsze od 10. | P | F |
Cosinus kąta 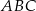 trójkąta trójkąta 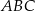 jest równy jest równy 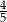 . . | P | F |

