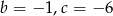Jednym z pierwiastków równania 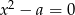 , gdzie
, gdzie  jest liczbą dodatnią, jest liczba
jest liczbą dodatnią, jest liczba 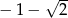 . Zatem liczba
. Zatem liczba  jest równa:
jest równa:
A) 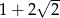 B)
B) 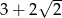 C)
C) 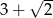 D) 0
D) 0
/Szkoła średnia/Zadania testowe/Równania/Kwadratowe
Miejscami zerowymi funkcji kwadratowej 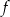 określonej wzorem
określonej wzorem 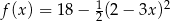 są liczby
są liczby
A) 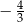 oraz
oraz 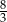 B)
B) 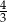 oraz
oraz 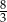 C)
C) 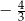 oraz
oraz 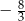 D)
D) 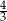 oraz
oraz 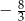
Równanie 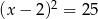 ma:
ma:
A) jedno rozwiązanie B) dwa rozwiązania C) nie ma rozwiązań D) cztery rozwiązania
Równanie 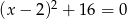 ma:
ma:
A) jedno rozwiązanie B) dwa rozwiązania C) nie ma rozwiązań D) cztery rozwiązania
Równanie 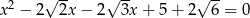
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dwa dodatnie rozwiązania rzeczywiste.
D) ma dwa ujemne rozwiązania rzeczywiste.
Liczba 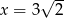 jest pierwiastkiem wielomianu
jest pierwiastkiem wielomianu 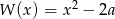 , gdy
, gdy  jest równe
jest równe
A) 18 B) 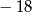 C) 9 D)
C) 9 D) 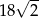
Jednym z pierwiastków równania 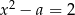 , gdzie
, gdzie  jest liczbą dodatnią, jest liczba
jest liczbą dodatnią, jest liczba 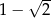 . Zatem drugim pierwiastkiem tego równania jest liczba:
. Zatem drugim pierwiastkiem tego równania jest liczba:
A) 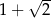 B)
B) 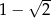 C)
C) 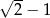 D) 0
D) 0
Rozwiązaniem równania 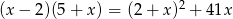 jest:
jest:
A) 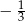 B)
B) 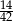 C)
C) 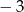 D)
D) 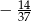
Rozwiązaniem równania 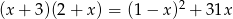 jest:
jest:
A) 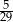 B)
B) 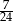 C)
C) 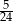 D)
D) 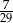
Liczba rozwiązań równania 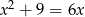 wynosi
wynosi
A) 0 B) 1 C) 2 D) 3
Równanie 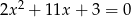
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dwa dodatnie rozwiązania rzeczywiste.
D) ma dwa ujemne rozwiązania rzeczywiste.
Równanie 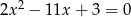
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dwa dodatnie rozwiązania rzeczywiste.
D) ma dwa ujemne rozwiązania rzeczywiste.
Pierwiastki trójmianu kwadratowego są liczbami przeciwnymi. Te warunki spełnia trójmian
A) 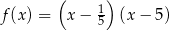 B)
B) 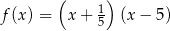
C) 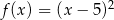 D)
D) 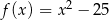
Pierwiastki trójmianu kwadratowego są liczbami odwrotnymi. Te warunki spełnia trójmian
A) 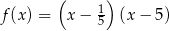 B)
B) 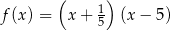
C) 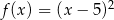 D)
D) 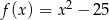
Pierwiastki trójmianu kwadratowego są liczbami przeciwnymi. Te warunki spełnia trójmian
A) 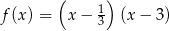 B)
B) 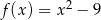
C) 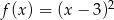 D)
D) 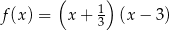
Liczby 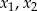 są rozwiązaniami równania
są rozwiązaniami równania 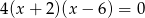 . Suma
. Suma 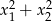 jest równa
jest równa
A) 16 B) 32 C) 40 D) 48
Funkcja kwadratowa jest określona wzorem 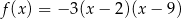 . Liczby
. Liczby 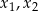 są różnymi miejscami zerowymi funkcji
są różnymi miejscami zerowymi funkcji 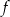 . Zatem
. Zatem
A) 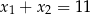 B)
B) 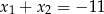 C)
C) 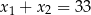 D)
D) 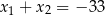
Funkcja kwadratowa jest określona wzorem 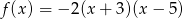 . Liczby
. Liczby 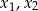 są różnymi miejscami zerowymi funkcji
są różnymi miejscami zerowymi funkcji 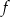 . Zatem
. Zatem
A) 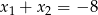 B)
B) 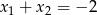 C)
C) 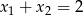 D)
D) 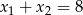
Liczby 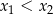 są rozwiązaniami równania
są rozwiązaniami równania 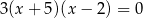 . Różnica
. Różnica 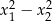 jest równa
jest równa
A) 21 B) 29 C) 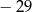 D)
D) 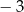
Pierwiastki 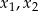 równania
równania 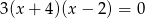 spełniają warunek
spełniają warunek
A) 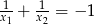 B)
B) 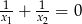 C)
C) 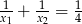 D)
D) 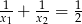
Pierwiastki 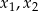 równania
równania 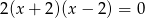 spełniają warunek
spełniają warunek
A) 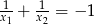 B)
B) 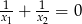 C)
C) 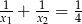 D)
D) 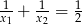
Jednym z miejsc zerowych funkcji kwadratowej 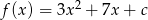 jest liczba
jest liczba 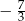 . Wówczas
. Wówczas  jest równe
jest równe
A) 0 B) 1 C) 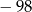 D) 98
D) 98
Jednym z miejsc zerowych funkcji kwadratowej 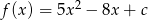 jest liczba
jest liczba  . Wówczas
. Wówczas  jest równe
jest równe
A) 1 B) 0 C) 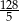 D)
D) 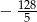
Równanie 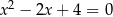
A) nie ma pierwiastków B) ma pierwiastki 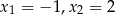
C) ma pierwiastki 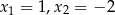 D) ma jeden pierwiastek
D) ma jeden pierwiastek
Równanie 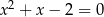
A) nie ma pierwiastków B) ma pierwiastki 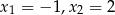
C) ma pierwiastki 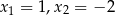 D) ma jeden pierwiastek
D) ma jeden pierwiastek
Równanie 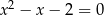
A) nie ma pierwiastków B) ma pierwiastki 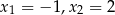
C) ma pierwiastki 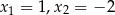 D) ma jeden pierwiastek
D) ma jeden pierwiastek
Równanie 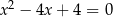
A) nie ma pierwiastków B) ma pierwiastki 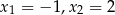
C) ma pierwiastki 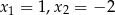 D) ma jeden pierwiastek
D) ma jeden pierwiastek
Jednym z pierwiastków równania 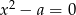 , gdzie
, gdzie  jest liczbą dodatnią, jest liczba
jest liczbą dodatnią, jest liczba 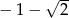 . Zatem drugim pierwiastkiem tego równania jest liczba:
. Zatem drugim pierwiastkiem tego równania jest liczba:
A) 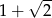 B)
B) 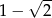 C)
C) 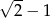 D)
D) 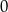
Liczby 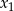 i
i 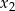 są pierwiastkami równania
są pierwiastkami równania 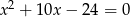 i
i 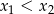 . Oblicz
. Oblicz 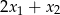 .
.
A) -22 B) -17 C) 8 D) 13
Liczby 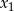 i
i 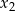 są pierwiastkami równania
są pierwiastkami równania 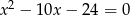 i
i 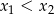 . Oblicz
. Oblicz 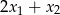 .
.
A) -22 B) -17 C) 8 D) 13
Funkcja kwadratowa jest określona wzorem 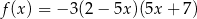 . Liczby
. Liczby 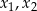 są różnymi miejscami zerowymi funkcji
są różnymi miejscami zerowymi funkcji 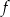 . Zatem
. Zatem
A) 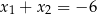 B)
B) 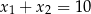 C)
C) 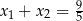 D)
D) 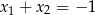
Funkcja 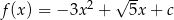 ma jedno miejsce zerowe. Zatem
ma jedno miejsce zerowe. Zatem
A) 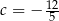 B)
B) 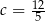 C)
C) 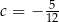 D)
D) 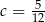
Równanie 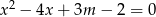 dokładnie jedno rozwiązanie gdy
dokładnie jedno rozwiązanie gdy
A) 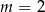 B)
B) 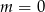 C)
C) 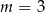 D)
D) 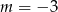
Funkcja kwadratowa 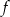 określona wzorem
określona wzorem 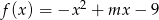 ma jedno miejsce zerowe. Zatem
ma jedno miejsce zerowe. Zatem
A) 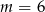 B)
B) 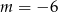 C)
C) 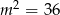 D)
D) 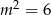
Miejscami zerowymi funkcji kwadratowej 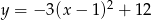 są
są
A) 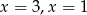 B)
B) 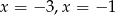 C)
C) 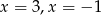 D)
D) 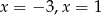
Miejscami zerowymi funkcji kwadratowej 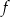 określonej wzorem
określonej wzorem 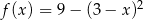 są liczby
są liczby
A) 0 oraz 3 B) 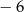 oraz 6 C) 0 oraz
oraz 6 C) 0 oraz 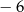 D) 0 oraz 6
D) 0 oraz 6
Miejscami zerowymi funkcji kwadratowej 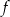 określonej wzorem
określonej wzorem 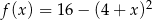 są liczby
są liczby
A) 0 oraz 4 B) 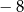 oraz 8 C) 0 oraz
oraz 8 C) 0 oraz 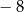 D)
D) 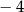 oraz 4
oraz 4
Funkcje kwadratowe 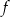 i
i 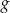 określone są wzorami
określone są wzorami 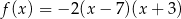 i
i 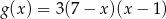 . Liczby
. Liczby 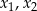 są różnymi miejscami zerowymi funkcji
są różnymi miejscami zerowymi funkcji 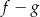 . Zatem
. Zatem
A) 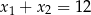 B)
B) 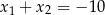 C)
C) 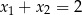 D)
D) 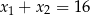
Pierwiastkami trójmianu kwadratowego 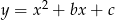 są liczby -4 i 6. Wynika stąd, że
są liczby -4 i 6. Wynika stąd, że
A) 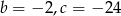 B)
B) 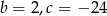 C)
C) 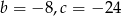 D)
D) 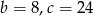
Pierwiastkami trójmianu kwadratowego 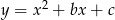 są liczby 4 i -6. Wynika stąd, że
są liczby 4 i -6. Wynika stąd, że
A) 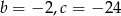 B)
B) 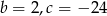 C)
C) 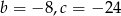 D)
D) 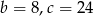
Pierwiastkami trójmianu kwadratowego 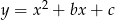 są liczby -2 i 3. Wynika stąd, że
są liczby -2 i 3. Wynika stąd, że
A) 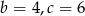 B)
B) 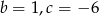 C)
C) 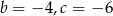 D)
D)