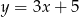Punkt 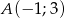 należy do wykresu funkcji:
należy do wykresu funkcji:
A) 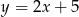 B)
B) 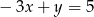 C)
C) 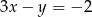 D)
D) 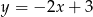
/Szkoła średnia/Zadania testowe/Funkcje - wykresy/Liniowy
Punkt 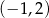 należy do wykresu funkcji
należy do wykresu funkcji 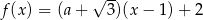 . Wynika stąd, że
. Wynika stąd, że
A) 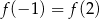 B)
B) 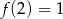 C)
C) 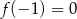 D)
D) 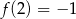
Na rysunku przedstawiony jest wykres funkcji liniowej  .
.
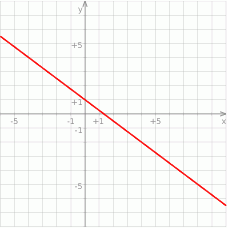
Funkcja 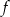 jest określona wzorem
jest określona wzorem
A) 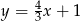 B)
B) 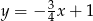 C)
C) 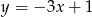 D)
D) 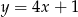
Wskaż wzór funkcji, której wykres przedstawiono na poniższym rysunku.
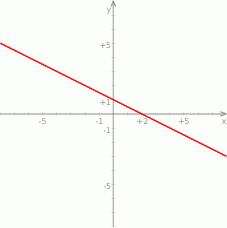
A) 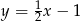 B)
B) 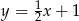 C)
C) 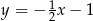 D)
D) 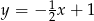
Na rysunku przedstawiony jest wykres funkcji liniowej  .
.
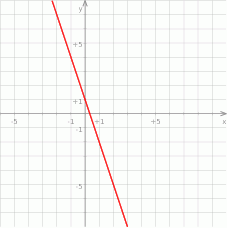
Funkcja 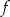 jest określona wzorem
jest określona wzorem
A) 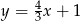 B)
B) 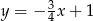 C)
C) 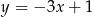 D)
D) 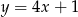
Na rysunku przedstawiony jest wykres funkcji liniowej 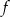 .
.
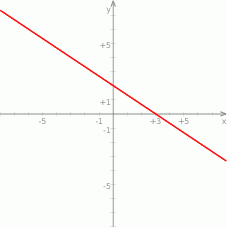
Funkcja 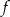 jest określona wzorem
jest określona wzorem
A) 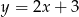 B)
B) 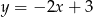 C)
C) 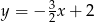 D)
D) 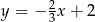
Wskaż wzór funkcji, której wykres przedstawiono na poniższym rysunku.
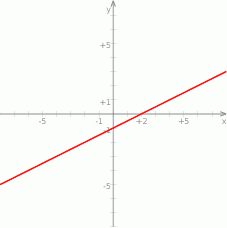
A) 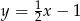 B)
B) 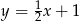 C)
C) 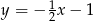 D)
D) 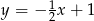
Wskaż wzór funkcji, której wykres przedstawiono na poniższym rysunku.
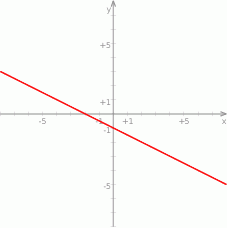
A) 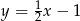 B)
B) 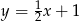 C)
C) 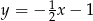 D)
D) 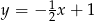
Na rysunku przedstawiony jest wykres funkcji liniowej 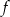 .
.
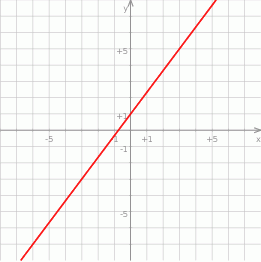
Funkcja 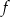 jest określona wzorem
jest określona wzorem
A) 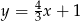 B)
B) 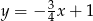 C)
C) 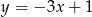 D)
D) 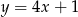
Na rysunku przedstawiony jest wykres funkcji liniowej 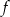 .
.
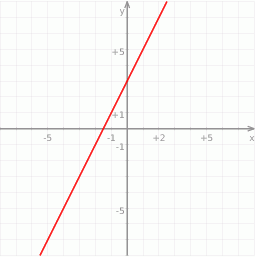
Funkcja 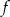 jest określona wzorem
jest określona wzorem
A) 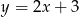 B)
B) 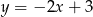 C)
C) 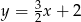 D)
D) 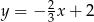
Na rysunku przedstawiony jest wykres funkcji liniowej 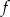 .
.
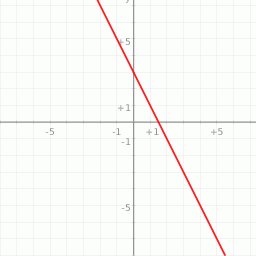
Funkcja 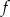 jest określona wzorem
jest określona wzorem
A) 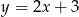 B)
B) 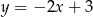 C)
C) 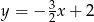 D)
D) 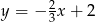
Na rysunku przedstawiono wykres funkcji 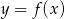 .
.
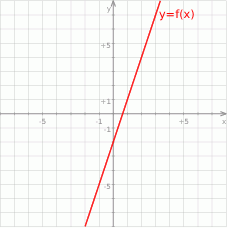
Wzór opisujący funkcję 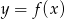 ma postać:
ma postać:
A) 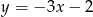 B)
B) 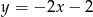 C)
C) 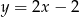 D)
D) 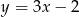
Do wykresu funkcji liniowej 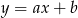 należą punkty
należą punkty 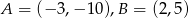 . Wynika stąd, że
. Wynika stąd, że
A) 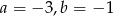 B)
B) 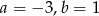 C)
C) 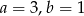 D)
D) 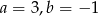
Jeżeli wiadomo, że punkty 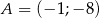 i
i 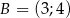 należą do wykresu funkcji liniowej, to ta funkcja opisana jest wzorem
należą do wykresu funkcji liniowej, to ta funkcja opisana jest wzorem
A) 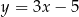 B)
B) 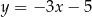 C)
C) 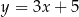 D)
D) 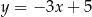
Do wykresu funkcji liniowej 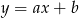 należą punkty
należą punkty 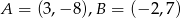 . Wynika stąd, że
. Wynika stąd, że
A) 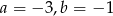 B)
B) 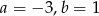 C)
C) 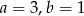 D)
D) 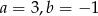
Do wykresu funkcji liniowej 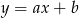 należą punkty
należą punkty 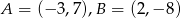 . Wynika stąd, że
. Wynika stąd, że
A) 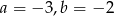 B)
B) 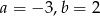 C)
C) 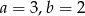 D)
D) 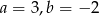
Do wykresu funkcji liniowej należą punkty 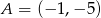 ,
, 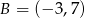 , zatem funkcja liniowa ma wzór
, zatem funkcja liniowa ma wzór
A) 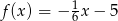 B)
B) 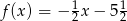 C)
C) 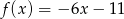 D)
D) 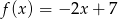
Funkcja liniowa 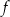 jest określona wzorem
jest określona wzorem 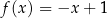 . Funkcja
. Funkcja 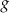 jest liniowa. W kartezjańskim układzie współrzędnych
jest liniowa. W kartezjańskim układzie współrzędnych 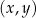 wykres funkcji
wykres funkcji 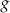 przechodzi przez punkt
przechodzi przez punkt 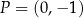 i jest prostopadły do wykresu funkcji
i jest prostopadły do wykresu funkcji 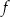 . Wzorem funkcji
. Wzorem funkcji 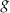 jest
jest
A) 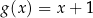 B)
B) 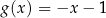 C)
C) 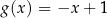 D)
D) 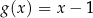
Funkcja liniowa 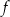 jest określona wzorem
jest określona wzorem 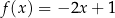 . Funkcja
. Funkcja 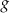 jest liniowa. W kartezjańskim układzie współrzędnych
jest liniowa. W kartezjańskim układzie współrzędnych 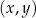 wykres funkcji
wykres funkcji 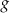 przechodzi przez punkt
przechodzi przez punkt 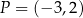 i jest prostopadły do wykresu funkcji
i jest prostopadły do wykresu funkcji 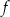 . Wzorem funkcji
. Wzorem funkcji 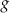 jest
jest
A) 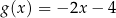 B)
B) 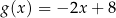 C)
C) 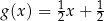 D)
D) 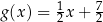
Podstawa 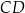 trapezu równoramiennego
trapezu równoramiennego 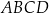 , który nie jest równoległobokiem, ma równanie
, który nie jest równoległobokiem, ma równanie 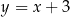 . Ponadto
. Ponadto 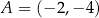 i
i 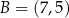 . Oś symetrii tego trapezu ma równanie
. Oś symetrii tego trapezu ma równanie
A) 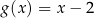 B)
B) 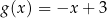 C)
C) 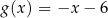 D)
D) 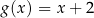
Do wykresu funkcji liniowej 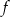 należą punkty
należą punkty 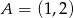 i
i 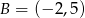 . Funkcja
. Funkcja 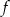 ma wzór
ma wzór
A) 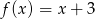 B)
B) 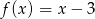 C)
C) 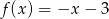 D)
D) 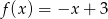
O funkcji liniowej 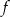 wiadomo, że
wiadomo, że 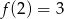 oraz punkt
oraz punkt 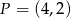 należy do jej wykresu. Wzór funkcji
należy do jej wykresu. Wzór funkcji 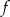 to
to
A) 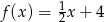 B)
B) 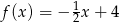 C)
C) 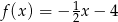 D)
D) 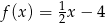
Do wykresu funkcji liniowej 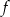 należą punkty
należą punkty 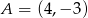 i
i 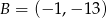 . Funkcja
. Funkcja 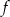 opisana jest wzorem
opisana jest wzorem
A) 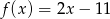 B)
B) 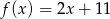 C)
C) 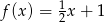 D)
D) 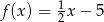
Do wykresu funkcji liniowej 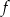 należą punkty
należą punkty 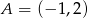 i
i 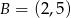 . Funkcja
. Funkcja 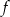 ma wzór
ma wzór
A) 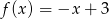 B)
B) 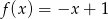 C)
C) 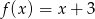 D)
D) 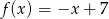
Do wykresu funkcji liniowej 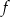 należą punkty
należą punkty 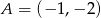 i
i 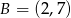 . Funkcja
. Funkcja 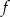 ma wzór
ma wzór
A) 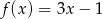 B)
B) 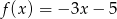 C)
C) 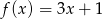 D)
D) 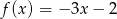
O funkcji liniowej 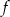 wiadomo, że
wiadomo, że 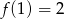 . Do wykresu tej funkcji należy punkt
. Do wykresu tej funkcji należy punkt 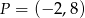 . Wzór funkcji
. Wzór funkcji 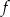 to
to
A) 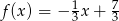 B)
B) 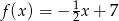 C)
C) 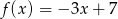 D)
D) 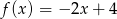
O funkcji liniowej 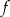 wiadomo, że
wiadomo, że 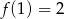 . Do wykresu tej funkcji należy punkt
. Do wykresu tej funkcji należy punkt 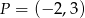 . Wzór funkcji
. Wzór funkcji 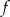 to
to
A) 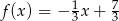 B)
B) 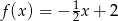 C)
C) 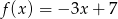 D)
D) 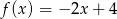
Przez punkty 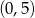 i
i 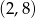 przechodzi wykres funkcji
przechodzi wykres funkcji
A) 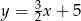 B)
B)  C)
C) 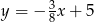 D)
D) 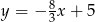
Przez punkty 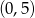 i
i 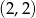 przechodzi wykres funkcji
przechodzi wykres funkcji
A) 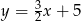 B)
B) 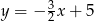 C)
C) 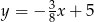 D)
D) 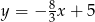
Przez punkty 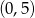 i
i 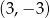 przechodzi wykres funkcji
przechodzi wykres funkcji
A) 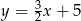 B)
B) 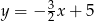 C)
C) 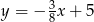 D)
D) 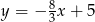
Do wykresu funkcji nie należy punkt 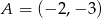 . Funkcja
. Funkcja 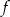 może mieć wzór
może mieć wzór
A) 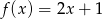 B)
B) 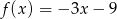 C)
C) 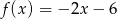 D)
D) 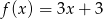
Na rysunku przedstawiony jest fragment wykresu funkcji liniowej 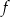 . Na wykresie tej funkcji leżą punkty
. Na wykresie tej funkcji leżą punkty 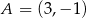 i
i 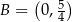 .
.
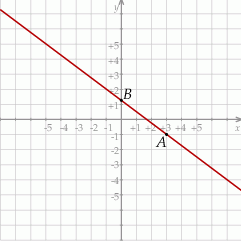
Obrazem prostej 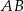 przy obrocie o kąt
przy obrocie o kąt 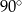 wokół punktu
wokół punktu 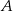 jest wykres funkcji
jest wykres funkcji 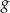 określonej wzorem
określonej wzorem
A) 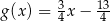 B)
B) 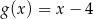 C)
C) 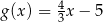 D)
D) 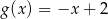
Gdy przesuniemy wykres funkcji 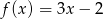 o 3 jednostki w prawo i 2 jednostki w górę, to otrzymamy wykres funkcji opisanej wzorem
o 3 jednostki w prawo i 2 jednostki w górę, to otrzymamy wykres funkcji opisanej wzorem
A) 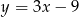 B)
B) 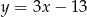 C)
C) 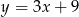 D)
D) 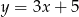
Aby otrzymać wykres funkcji 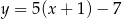 , należało wykres funkcji
, należało wykres funkcji 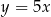 przesunąć
przesunąć
A) o 1 jednostkę w lewo i 7 ku dołowi B) o 1 jednostkę w prawo i 7 ku górze
C) o 1 jednostkę w prawo i 7 ku dołowi D) o 1 jednostkę w lewo i 7 ku górze
Gdy przesuniemy wykres funkcji 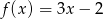 o 3 jednostki w lewo i 2 jednostki w dół, to otrzymamy wykres funkcji opisanej wzorem
o 3 jednostki w lewo i 2 jednostki w dół, to otrzymamy wykres funkcji opisanej wzorem
A) 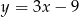 B)
B) 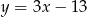 C)
C) 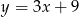 D)
D)