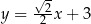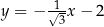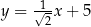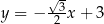Okrąg o równaniu 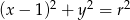 , gdzie
, gdzie 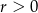 , ma z prostą
, ma z prostą 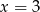 dwa punkty wspólne. Zatem
dwa punkty wspólne. Zatem
A) 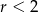 B)
B) 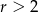 C)
C) 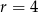 D)
D) 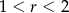
/Szkoła średnia/Zadania testowe/Geometria
Okrąg o równaniu 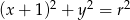 , gdzie
, gdzie 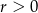 , ma z prostą
, ma z prostą 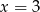 dwa punkty wspólne. Zatem
dwa punkty wspólne. Zatem
A) 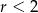 B)
B) 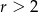 C)
C) 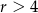 D)
D) 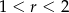
Okrąg o równaniu 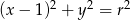 , gdzie
, gdzie 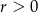 , ma z prostą
, ma z prostą 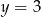 dwa punkty wspólne. Zatem
dwa punkty wspólne. Zatem
A) 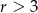 B)
B) 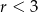 C)
C) 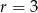 D)
D) 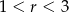
Okrąg o równaniu 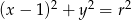 , gdzie
, gdzie 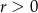 , nie przecina prostej
, nie przecina prostej 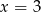 . Zatem
. Zatem
A) 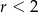 B)
B) 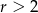 C)
C) 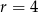 D)
D) 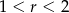
Pole rombu o obwodzie 8 jest równe 1. Kąt ostry tego rombu ma miarę  . Wtedy
. Wtedy
A) 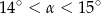 B)
B) 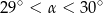 C)
C) 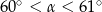 D)
D) 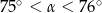
Pole rombu o obwodzie 40 jest równe 35. Kąt ostry tego rombu ma miarę  . Wtedy
. Wtedy
A) 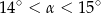 B)
B) 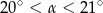 C)
C) 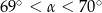 D)
D) 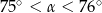
W równoległoboku 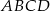 dłuższa podstawa ma długość
dłuższa podstawa ma długość 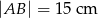 . Wysokości tego równoległoboku mają długości:
. Wysokości tego równoległoboku mają długości: 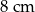 i
i 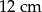 . Zatem krótsza podstawa równoległoboku ma długość
. Zatem krótsza podstawa równoległoboku ma długość
A) 20 cm B) 10 cm C) 3,2 cm D) 1,6 cm
W trójkącie prostokątnym długości przyprostokątnych wynoszą 6 i 8. Stosunek długości odcinków, na które wysokość podzieliła przeciwprostokątną wynosi
A)  B)
B)  C)
C) 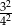 D)
D) 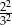
Dany jest trójkąt prostokątny o przyprostokątnych 5 i 12. Poprowadzono wysokość na przeciwprostokątną. Wysokość ta podzieliła przeciwprostokątną na odcinki w stosunku
A) 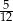 B)
B) 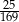 C)
C) 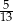 D)
D) 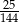
Dane są punkty 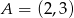 oraz
oraz 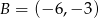 . Promień okręgu wpisanego w trójkąt równoboczny
. Promień okręgu wpisanego w trójkąt równoboczny 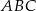 jest równy
jest równy
A) 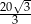 B)
B) 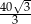 C)
C) 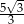 D)
D) 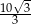
Liczba przekątnych siedmiokąta foremnego jest równa
A) 7 B) 14 C) 21 D) 28
Liczba przekątnych sześciokąta foremnego jest równa
A) 9 B) 14 C) 18 D) 6
Suma liczby wierzchołków i liczby krawędzi graniastosłupa może być równa
A) 2017 B) 2016 C) 2015 D) 2014
Punkty: 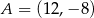 ,
, 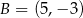 ,
, 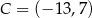 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 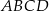 . Wierzchołek
. Wierzchołek 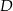 tego równoległoboku ma współrzędne
tego równoległoboku ma współrzędne
A) 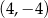 B)
B) 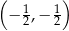 C)
C) 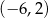 D)
D) 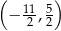
Trójkąt można zbudować z odcinków o długościach:
A) 10, 6, 5 B) 4, 2, 1 C) 8, 5, 3 D) 6, 6, 13
Trójkąt można zbudować z odcinków o długościach:
A) 4, 2, 2 B) 7, 4, 3 C) 5, 6, 12 D) 8, 4, 5
Jeśli 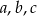 są długościami odcinków, to istnieje trójkąt o bokach
są długościami odcinków, to istnieje trójkąt o bokach 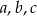 , jeżeli
, jeżeli
A) 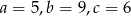
B) 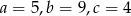
C) 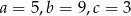
D) 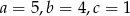
Można zbudować trójkąt z odcinków 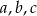 jeśli
jeśli
A) 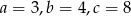
B) 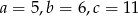
C) 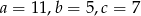
D) 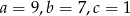
Długościami boków trójkąta mogą być odcinki:
A) 5 cm, 8 cm, 2 cm B) 9 cm, 4 cm, 4 cm C) 3 cm, 2 cm, 1 cm D) 7 cm, 9 cm, 10 cm
Punkty 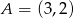 i
i 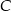 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 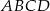 , a punkt
, a punkt 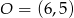 jest środkiem okręgu opisanego na tym kwadracie. Współrzędne punktu
jest środkiem okręgu opisanego na tym kwadracie. Współrzędne punktu 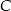 są równe
są równe
A) 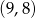 B)
B) 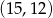 C)
C) 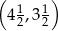 D)
D) 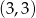
W kartezjańskim układzie współrzędnych 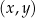 proste o równaniach:
proste o równaniach:
przecinają się w punktach, które są wierzchołkami czworokąta 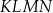 . Czworokąt
. Czworokąt 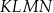 jest
jest
| A) | prostokątem, |
| B) | trapezem, który nie jest równoległobokiem |
| C) | równoległobokiem, który nie jest prostokątem, |
ponieważ
| 1) | czworokąt 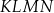 ma dwie osie symetrii. ma dwie osie symetrii. |
| 2) | dwie z tych prostych są prostopadłe. |
| 3) | dwie z tych prostych są równoległe. |
O ile 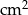 zwiększy się pole prostokąta o wymiarach
zwiększy się pole prostokąta o wymiarach  cm i
cm i 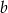 cm, jeżeli bok długości
cm, jeżeli bok długości  cm zwiększymy 2 razy, a bok długości
cm zwiększymy 2 razy, a bok długości 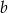 cm zwiększymy o 20%?
cm zwiększymy o 20%?
A) 2,4 B) 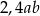 C)
C) 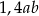 D) 1,4
D) 1,4
O ile 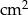 zwiększy się pole prostokąta o wymiarach
zwiększy się pole prostokąta o wymiarach 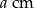 i
i 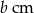 , jeżeli bok długości
, jeżeli bok długości  cm zwiększymy o 130%, a bok długości
cm zwiększymy o 130%, a bok długości 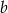 cm zwiększymy o 20%?
cm zwiększymy o 20%?
A) 2,76 B) 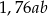 C)
C) 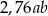 D) 1,76
D) 1,76
O ile 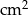 zwiększy się pole prostokąta o wymiarach
zwiększy się pole prostokąta o wymiarach 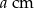 i
i 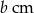 , jeżeli bok długości
, jeżeli bok długości 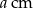 zwiększymy o 100%, a bok długości
zwiększymy o 100%, a bok długości 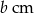 zwiększymy o 20%?
zwiększymy o 20%?
A) 2,4 B) 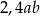 C)
C) 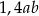 D) 1,4
D) 1,4
Jedna z przekątnych kwadratu 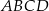 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 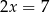 oraz
oraz 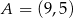 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 121 B) 24,5 C) 60,5 D) 49
Punkty 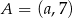 ,
, 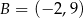 i
i 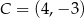 są wierzchołkami trójkąta równoramiennego o podstawie
są wierzchołkami trójkąta równoramiennego o podstawie 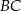 . Zatem
. Zatem
A) 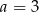 B)
B) 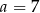 C)
C) 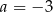 D)
D) 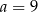
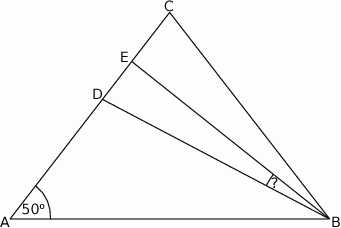
W trójkącie równoramiennym 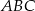 spełnione są warunki:
spełnione są warunki: 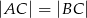 ,
, 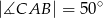 . Odcinek
. Odcinek 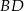 jest dwusieczną kąta
jest dwusieczną kąta 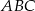 , a odcinek
, a odcinek 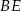 jest wysokością opuszczoną z wierzchołka
jest wysokością opuszczoną z wierzchołka 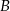 na bok
na bok 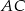 . Miara kąta
. Miara kąta 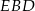 jest równa
jest równa
A) 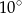 B)
B) 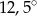 C)
C) 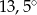 D)
D) 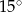
Suma długości wszystkich krawędzi sześcianu jest równa 24. Pole powierzchni tego sześcianu jest równe
A) 4 B) 16 C) 24 D) 8
Suma długości wszystkich krawędzi sześcianu jest równa 96 cm. Pole powierzchni całkowitej tego sześcianu jest równe
A) 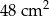 B)
B) 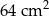 C)
C) 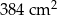 D)
D) 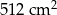
Suma długości wszystkich krawędzi sześcianu jest równa 108 cm. Pole powierzchni całkowitej tego sześcianu jest równe
A) 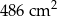 B)
B) 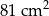 C)
C) 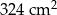 D)
D) 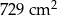
W trójkącie prostokątnym spodek wysokości poprowadzonej na przeciwprostokątną podzielił ją na odcinki długości 6,25 cm oraz 16 cm. Zatem wysokość ta ma długość
A) 15 cm B) 20 cm C) 22,25 cm D) 10 cm
W trójkącie prostokątnym spodek wysokości poprowadzonej na przeciwprostokątną podzielił ją na odcinki długości 3 cm oraz 12 cm. Zatem wysokość ta ma długość
A) 6 cm B) 20 cm C) 22,25 cm D) 10 cm
W trójkącie prostokątnym spodek wysokości poprowadzonej na przeciwprostokątną podzielił ją na odcinki długości 5,5 cm oraz 22 cm. Zatem wysokość ta ma długość
A) 15 cm B) 11 cm C) 22,25 cm D) 10 cm
Przekątna ściany sześcianu ma długość 2. Pole powierzchni całkowitej tego sześcianu jest równe
A) 24 B) 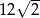 C) 12 D)
C) 12 D) 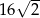
W trapezie 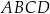 o podstawach
o podstawach 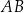 i
i 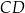 przekątne przecinają się w punkcie
przekątne przecinają się w punkcie 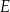 (zobacz rysunek).
(zobacz rysunek).
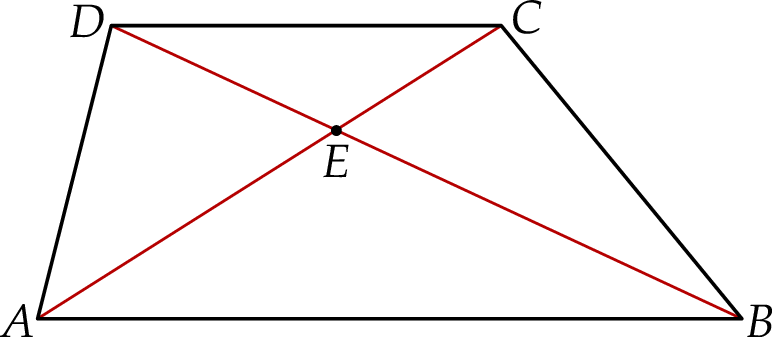
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 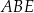 jest podobny do trójkąta jest podobny do trójkąta 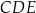 . . | P | F |
Pole trójkąta 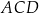 jest równe polu trójkąta jest równe polu trójkąta 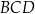 . . | P | F |
W trapezie 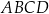 podstawa
podstawa 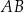 jest dłuższa od podstawy
jest dłuższa od podstawy 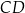 . Przekątne trapezu przecinają się w punkcie
. Przekątne trapezu przecinają się w punkcie 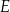 (zobacz rysunek).
(zobacz rysunek).
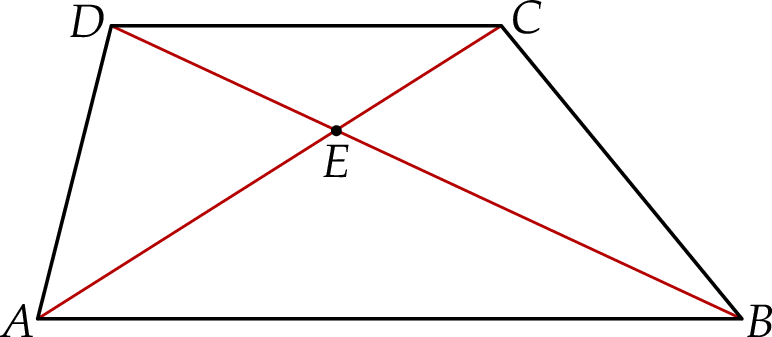
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta 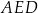 jest równe polu trójkąta jest równe polu trójkąta 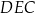 . . | P | F |
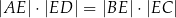 | P | F |
Na rysunku przedstawiono okrąg o środku 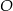 , który jest wpisany w trójkąt
, który jest wpisany w trójkąt 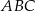 .
.
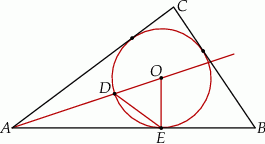
Okrąg ten przecina bok 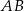 w punkcie
w punkcie 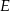 , a odcinek
, a odcinek 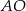 w punkcie
w punkcie 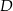 . Jeżeli
. Jeżeli 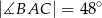 , to miara kąta
, to miara kąta 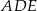 jest równa
jest równa
A) 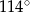 B)
B) 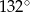 C)
C) 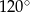 D)
D)