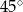Odległości punktu 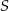 przecięcia przekątnych czworokąta przedstawionego na rysunku od wierzchołków
przecięcia przekątnych czworokąta przedstawionego na rysunku od wierzchołków 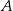 i
i 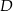 są równe
są równe 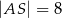 i
i 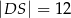 . Bok
. Bok 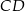 tego czworokąta ma długość
tego czworokąta ma długość
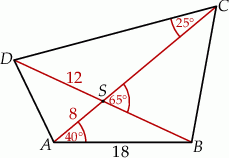
A) 27 B) 16 C) 24 D) 30
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Odległości punktu 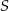 przecięcia przekątnych czworokąta przedstawionego na rysunku od wierzchołków
przecięcia przekątnych czworokąta przedstawionego na rysunku od wierzchołków 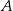 i
i 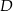 są równe
są równe 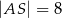 i
i 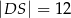 . Bok
. Bok 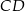 tego czworokąta ma długość
tego czworokąta ma długość

A) 27 B) 16 C) 24 D) 30
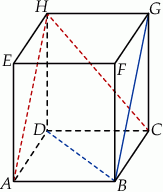
Podstawą graniastosłupa prostego czworokątnego 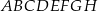 jest kwadrat
jest kwadrat 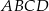 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 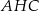 między przekątnymi sąsiednich ścian bocznych ma miarę
między przekątnymi sąsiednich ścian bocznych ma miarę 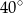 . Kąt
. Kąt 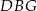 między przekątną podstawy, a przekątną ściany bocznej ma miarę
między przekątną podstawy, a przekątną ściany bocznej ma miarę
A) 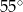 B)
B) 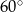 C)
C) 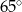 D)
D) 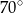
Podstawą graniastosłupa prostego czworokątnego 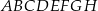 jest kwadrat
jest kwadrat 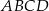 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 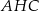 między przekątnymi sąsiednich ścian bocznych ma miarę
między przekątnymi sąsiednich ścian bocznych ma miarę 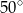 . Kąt
. Kąt 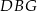 między przekątną podstawy, a przekątną ściany bocznej ma miarę
między przekątną podstawy, a przekątną ściany bocznej ma miarę
A)  B)
B)  C)
C) 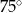 D)
D) 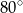
Podstawą graniastosłupa prawidłowego czworokątnego jest kwadrat o boku długości 4. Przekątna tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 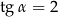 .
.
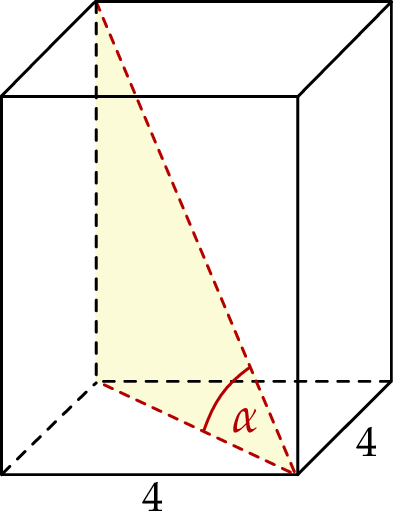
Wysokość tego graniastosłupa jest równa
A) 2 B) 8 C) 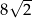 D)
D) 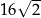
Punkt 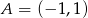 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 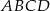 , którego bok
, którego bok 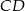 zawiera się w prostej
zawiera się w prostej 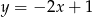 . Podstawa
. Podstawa 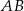 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 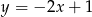 B)
B) 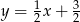 C)
C) 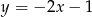 D)
D) 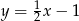
Punkt 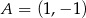 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 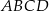 , którego bok
, którego bok 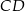 zawiera się w prostej
zawiera się w prostej 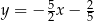 . Podstawa
. Podstawa 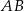 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A)  B)
B) 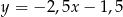 C)
C) 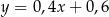 D)
D) 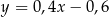
Punkt 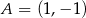 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 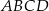 , którego bok
, którego bok 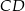 zawiera się w prostej
zawiera się w prostej 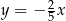 . Podstawa
. Podstawa 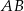 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 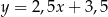 B)
B) 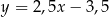 C)
C) 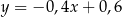 D)
D) 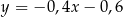
Podstawą prostopadłościanu jest prostokąt o wymiarach 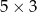 , a jego pole powierzchni całkowitej jest równe 94. Wysokość tego prostopadłościanu ma długość
, a jego pole powierzchni całkowitej jest równe 94. Wysokość tego prostopadłościanu ma długość
A) 2 B) 3 C) 4 D) 5
Naprzeciwko boków 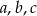 trójkąta
trójkąta 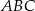 znajdują się odpowiednio kąty
znajdują się odpowiednio kąty 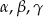 . Wiadomo, że
. Wiadomo, że 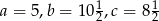 . Wówczas
. Wówczas
A) 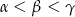 B)
B) 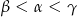 C)
C) 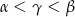 D)
D) 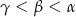
Naprzeciwko boków 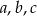 trójkąta
trójkąta 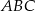 znajdują się odpowiednio kąty
znajdują się odpowiednio kąty 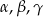 . Wiadomo, że
. Wiadomo, że 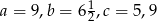 . Wówczas
. Wówczas
A) 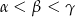 B)
B) 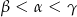 C)
C) 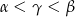 D)
D) 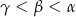
Naprzeciwko boków 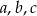 trójkąta
trójkąta 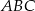 znajdują się odpowiednio kąty
znajdują się odpowiednio kąty 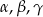 . Wiadomo, że
. Wiadomo, że 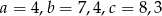 . Wówczas
. Wówczas
A) 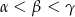 B)
B) 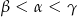 C)
C) 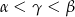 D)
D) 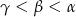
Dane są punkty 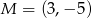 oraz
oraz 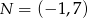 . Prosta przechodząca przez te punkty ma równanie
. Prosta przechodząca przez te punkty ma równanie
A) 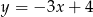 B)
B) 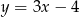 C)
C) 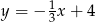 D)
D) 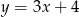
Prosta przechodząca przez punkty 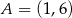 i
i 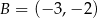 jest określona równaniem
jest określona równaniem
A) 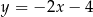 B)
B) 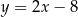 C)
C) 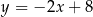 D)
D) 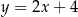
Prosta przechodząca przez punkty 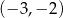 oraz
oraz 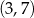 ma równanie
ma równanie
A) 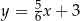 B)
B) 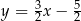 C)
C) 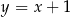 D)
D) 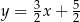
Prosta przechodząca przez punkty 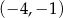 oraz
oraz 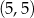 ma równanie
ma równanie
A) 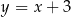 B)
B) 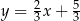 C)
C) 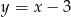 D)
D) 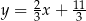
Prosta przechodząca przez punkty 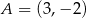 i
i 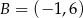 jest określona równaniem
jest określona równaniem
A) 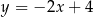 B)
B) 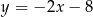 C)
C) 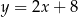 D)
D) 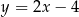
Ostrosłup prawidłowy ma 2024 ściany boczne. Liczba wszystkich krawędzi tego ostrosłupa jest równa
A) 2025 B) 2026 C) 4048 D) 4052
Pole powierzchni całkowitej pewnego stożka jest 3 razy większe od pola powierzchni pewnej kuli. Promień tej kuli jest równy 2 i jest taki sam jak promień podstawy tego stożka. Tworząca tego stożka ma długość równą
A) 12 B) 11 C) 24 D) 22
Pole powierzchni całkowitej pewnego stożka jest 4 razy większe od pola powierzchni pewnej kuli. Promień tej kuli jest równy 3 i jest taki sam jak promień podstawy tego stożka. Tworząca tego stożka ma długość równą
A) 42 B) 45 C) 48 D) 52
Punkty 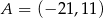 i
i 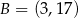 są końcami odcinka
są końcami odcinka 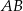 . Obrazem tego odcinka w symetrii względem osi
. Obrazem tego odcinka w symetrii względem osi 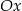 układu współrzędnych jest odcinek
układu współrzędnych jest odcinek 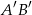 . Środkiem odcinka
. Środkiem odcinka 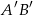 jest punkt o współrzędnych
jest punkt o współrzędnych
A) 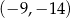 B)
B) 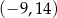 C)
C) 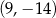 D)
D) 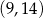
Punkty 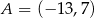 i
i 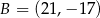 są końcami odcinka
są końcami odcinka 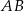 . Obrazem tego odcinka w symetrii względem osi
. Obrazem tego odcinka w symetrii względem osi 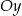 układu współrzędnych jest odcinek
układu współrzędnych jest odcinek 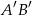 . Środkiem odcinka
. Środkiem odcinka 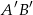 jest punkt o współrzędnych
jest punkt o współrzędnych
A) 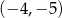 B)
B) 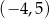 C)
C) 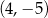 D)
D) 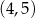
Przekątna sześcianu jest o 2 dłuższa od przekątnej ściany sześcianu. Wówczas krawędź sześcianu jest równa
A) 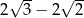 B)
B) 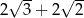 C)
C) 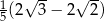 D)
D) 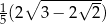
Przekątna sześcianu jest o 3 większa od przekątnej ściany sześcianu. Wówczas krawędź sześcianu jest równa
A) 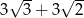 B)
B) 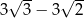 C)
C) 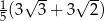 D)
D) 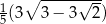
Przekątna sześcianu jest o 5 większa od przekątnej ściany sześcianu. Wówczas krawędź sześcianu jest równa
A) 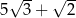 B)
B) 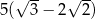 C)
C) 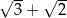 D)
D) 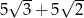
Ostrosłup ma 7 wierzchołków. Liczba jego ścian jest równa
A) 6 B) 7 C) 11 D) 12
Ostrosłup ma 8 wierzchołków. Liczba jego ścian jest równa
A) 6 B) 7 C) 8 D) 12
Ostrosłup ma 10 wierzchołków. Liczba jego ścian jest równa
A) 8 B) 9 C) 10 D) 6
Miary kątów trójkąta pozostają w stosunku 4:5:6. Miary kątów tego trójkąta są równe
A) 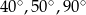 B)
B) 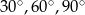 C)
C) 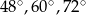 D)
D) 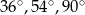
Pole powierzchni bocznej walca jest równe 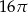 , a promień jego podstawy ma długość 2. Wysokość tego walca jest równa
, a promień jego podstawy ma długość 2. Wysokość tego walca jest równa
A) 4 B) 8 C) 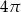 D)
D) 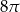
Pole powierzchni bocznej walca jest równe 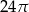 , a promień jego podstawy ma długość 4. Wysokość tego walca jest równa
, a promień jego podstawy ma długość 4. Wysokość tego walca jest równa
A) 6 B) 3 C) 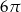 D)
D) 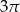
Hania zaprojektowała i wykonała czapeczkę na bal urodzinowy młodszego brata. Czapeczka miała kształt powierzchni bocznej stożka o średnicy podstawy 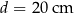 , wysokości
, wysokości 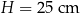 i tworzącej
i tworzącej 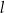 . Żeby wykonać czapeczkę, Hania najpierw narysowała na kartonie figurę płaską
. Żeby wykonać czapeczkę, Hania najpierw narysowała na kartonie figurę płaską 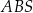 o kształcie wycinka koła o promieniu
o kształcie wycinka koła o promieniu 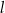 i środku
i środku 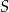 . Następnie wycięła tę figurę z kartonu, odpowiednio ją wymodelowała i skleiła odcinek
. Następnie wycięła tę figurę z kartonu, odpowiednio ją wymodelowała i skleiła odcinek 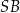 z odcinkiem
z odcinkiem 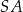 .
.

Kąt rozwarcia stożka, którego powierzchnią boczną jest czapeczka, ma miarę (w zaokrągleniu do 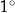 )
)
A) 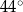 B)
B) 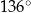 C)
C) 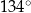 D)
D) 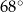
W okrąg o równaniu 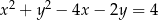 wpisano trójkąt równoramienny, w którym ramię tworzy z podstawą kąt o mierze
wpisano trójkąt równoramienny, w którym ramię tworzy z podstawą kąt o mierze 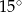 . Podstawa tego trójkąta ma długość
. Podstawa tego trójkąta ma długość
A) 1,5 B) 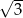 C) 3 D)
C) 3 D) 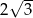
Dwa stożki o takich samych podstawach połączono podstawami w taki sposób jak na rysunku. Stosunek wysokości tych stożków jest równy 3 : 2. Objętość stożka o krótszej wysokości jest równa 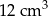 .
.
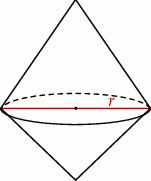
Objętość bryły utworzonej z połączonych stożków jest równa
A) 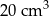 B)
B) 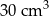 C)
C) 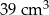 D)
D) 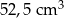
Dwa stożki o takich samych podstawach połączono podstawami w taki sposób jak na rysunku. Stosunek wysokości tych stożków jest równy 3 : 4. Objętość stożka o dłuższej wysokości jest równa 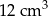 .
.
Objętość bryły utworzonej z połączonych stożków jest równa
A) 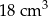 B)
B) 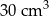 C)
C) 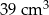 D)
D) 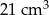
Proste o równaniach 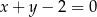 i
i 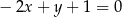 przecinają się w punkcie o współrzędnych
przecinają się w punkcie o współrzędnych
A) 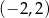 B)
B) 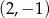 C)
C) 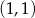 D)
D) 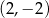
Proste o równaniach 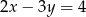 i
i 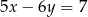 przecinają się w punkcie
przecinają się w punkcie 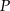 . Stąd wynika, że
. Stąd wynika, że
A) 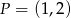 B)
B) 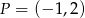 C)
C) 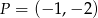 D)
D) 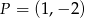
Proste o równaniach 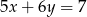 i
i 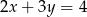 przecinają się w punkcie
przecinają się w punkcie 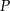 . Stąd wynika, że
. Stąd wynika, że
A) 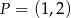 B)
B) 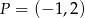 C)
C) 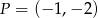 D)
D) 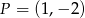
Boki równoległoboku są zawarte w prostych o równaniach: 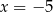 ,
, 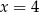 ,
, 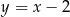 ,
, 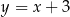 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 45 B) 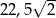 C)
C) 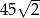 D) 22,5
D) 22,5
Punkty 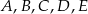 leżą na okręgu o środku
leżą na okręgu o środku 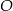 , przy czym
, przy czym 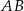 jest średnicą tego okręgu,
jest średnicą tego okręgu, 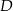 jest środkiem łuku
jest środkiem łuku 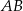 oraz
oraz 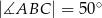 .
.
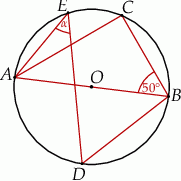
Miara kąta oznaczonego na rysunku literą  jest równa
jest równa
A) 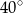 B)
B) 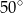 C)
C) 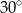 D)
D)