Na płaszczyźnie dany jest czworokąt 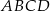 .
.
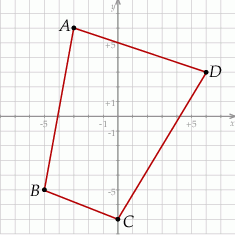
Który wierzchołek tego czworokąta jest położony najdalej od początku układu współrzędnych?
A) 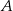 B)
B) 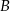 C)
C)  D)
D) 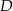
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na płaszczyźnie dany jest czworokąt 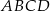 .
.

Który wierzchołek tego czworokąta jest położony najdalej od początku układu współrzędnych?
A) 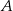 B)
B) 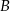 C)
C)  D)
D) 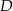
Punkty 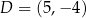 i
i 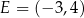 są wierzchołkami sześciokąta foremnego
są wierzchołkami sześciokąta foremnego 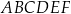 . Pole tego sześciokąta jest równe
. Pole tego sześciokąta jest równe
A) 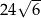 B)
B) 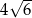 C)
C) 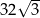 D)
D) 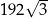
Wskaż równanie okręgu stycznego do prostej 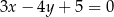 .
.
A) 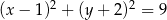 B)
B) 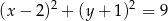
C) 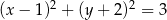 D)
D) 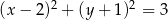
Przekątna sześcianu ma długość 3. Pole powierzchni całkowitej tego sześcianu jest równe
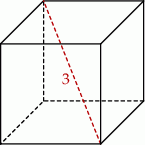
A) 54 B) 36 C) 18 D) 12
Długość przekątnej sześcianu jest równa 6. Stąd wynika, że pole powierzchni całkowitej tego sześcianu jest równe
A) 72 B) 48 C) 152 D) 108
Przekątna sześcianu ma długość 8. Pole powierzchni całkowitej tego sześcianu jest równe
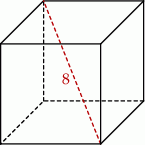
A) 128 B) 64 C) 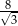 D)
D) 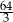
Jeżeli długość przekątnej sześcianu wynosi 3, to pole powierzchni całkowitej tego sześcianu jest równe
A) 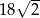 B) 24 C)
B) 24 C) 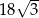 D) 18
D) 18
Przekątna sześcianu ma długość 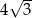 . Pole powierzchni tego sześcianu jest równe
. Pole powierzchni tego sześcianu jest równe
A) 96 B) 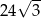 C) 192 D)
C) 192 D) 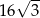
Przekątna sześcianu ma długość 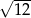 . Pole powierzchni tego sześcianu jest równe
. Pole powierzchni tego sześcianu jest równe
A) 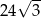 B) 24 C) 12 D)
B) 24 C) 12 D) 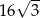
Ramię trójkąta równoramiennego 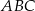 ma długość 8 cm i tworzy z podstawą kąt o mierze
ma długość 8 cm i tworzy z podstawą kąt o mierze 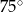 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 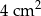 B)
B) 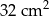 C)
C) 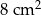 D)
D) 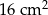
Dany jest trójkąt równoramienny, w którym ramię o długości 10 tworzy z podstawą kąt 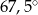 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 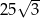 B)
B) 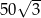 C)
C) 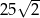 D)
D) 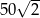
w trójkącie równoramiennym ramię ma długość 16 i tworzy z podstawą trójkąta kąt o mierze 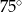 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 128 B) 64 C) 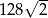 D)
D) 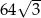
Dany jest trójkąt równoramienny, w którym ramię o długości 20 tworzy z podstawą kąt 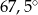 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 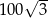 B)
B) 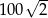 C)
C) 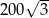 D)
D) 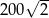
Punkty 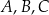 leżą na okręgu o środku
leżą na okręgu o środku 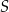 . Punkt
. Punkt 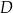 jest punktem przecięcia cięciwy
jest punktem przecięcia cięciwy 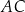 i średnicy okręgu poprowadzonej z punktu
i średnicy okręgu poprowadzonej z punktu 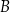 . Miara kąta
. Miara kąta 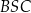 jest równa
jest równa  , a miara kąta
, a miara kąta 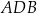 jest równa
jest równa 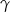 (zobacz rysunek).
(zobacz rysunek).

Wtedy kąt 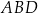 ma miarę
ma miarę
A) 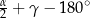 B)
B) 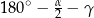 C)
C) 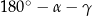 D)
D) 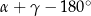
Przez punkt przecięcia wysokości trójkąta równobocznego 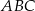 poprowadzono prostą
poprowadzono prostą 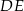 równoległą do podstawy
równoległą do podstawy 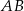 (zobacz rysunek).
(zobacz rysunek).
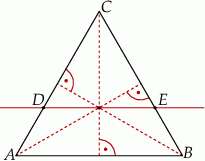
Stosunek pola trójkąta 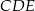 do pola trapezu
do pola trapezu 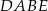 jest równy
jest równy
A) 5 : 9 B) 4 : 5 C) 4 : 9 D) 3 : 2
Wysokość ściany bocznej opuszczona na krawędź podstawy ostrosłupa prawidłowego trójkątnego jest 3 razy dłuższa od krawędzi jego podstawy. Stosunek pola powierzchni bocznej do pola powierzchni podstawy tego ostrosłupa jest równy
A) 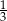 B)
B) 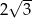 C)
C) 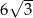 D) 9
D) 9
Punkt 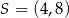 jest środkiem odcinka
jest środkiem odcinka 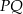 , którego koniec
, którego koniec 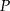 leży na osi
leży na osi 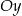 , a koniec
, a koniec 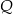 – na osi
– na osi 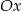 . Wynika stąd, że
. Wynika stąd, że
A) 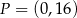 i
i 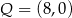 B)
B) 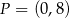 i
i 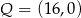
C) 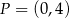 i
i 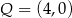 D)
D) 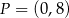 i
i 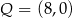
Punkt 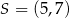 jest środkiem odcinka
jest środkiem odcinka 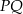 , którego koniec
, którego koniec 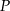 leży na osi
leży na osi 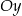 , a koniec
, a koniec 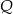 – na osi
– na osi 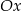 . Wynika stąd, że
. Wynika stąd, że
A) 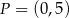 i
i 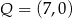 B)
B) 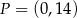 i
i 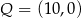
C) 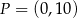 i
i 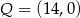 D)
D) 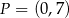 i
i 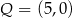
Obrazem prostej o równaniu 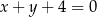 w symetrii osiowej względem prostej
w symetrii osiowej względem prostej 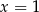 jest prosta o równaniu
jest prosta o równaniu
A) 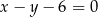 B)
B) 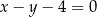 C)
C) 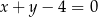 D)
D) 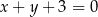
Wysokość rombu jest dwa razy krótsza od jego boku. Kąt rozwarty rombu ma miarę:
A) 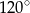 B)
B) 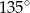 C)
C) 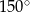 D)
D) 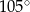
Prosta 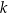 jest styczna w punkcie
jest styczna w punkcie 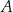 do okręgu opisanego na trójkącie równoramiennym
do okręgu opisanego na trójkącie równoramiennym 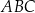 , w którym
, w którym 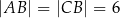 . Prosta
. Prosta 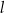 zawiera punkty
zawiera punkty 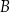 i
i 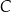 i przecina prostą
i przecina prostą 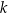 w punkcie
w punkcie 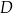 , przy czym
, przy czym 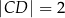 i
i 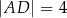 (zobacz rysunek).
(zobacz rysunek).

Długość odcinka 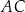 jest równa
jest równa
A) 3 B)  C)
C) 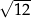 D)
D) 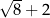
Suma długości wszystkich krawędzi czworościanu foremnego jest równa 12 cm. Pole powierzchni całkowitej tego czworościanu jest równe
A) 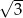 B)
B) 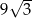 C)
C) 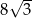 D)
D) 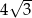
Punkt 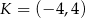 jest końcem odcinka
jest końcem odcinka 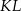 , punkt
, punkt 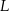 leży na osi
leży na osi 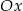 , a środek
, a środek 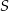 tego odcinka leży na osi
tego odcinka leży na osi 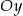 . Wynika stąd, że
. Wynika stąd, że
A) 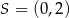 B)
B) 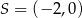 C)
C) 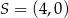 D)
D) 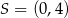
Punkt 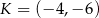 jest końcem odcinka
jest końcem odcinka 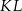 , punkt
, punkt 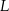 leży na osi
leży na osi 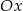 , a środek
, a środek 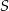 tego odcinka leży na osi
tego odcinka leży na osi 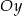 . Wynika stąd, że
. Wynika stąd, że
A) 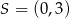 B)
B) 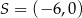 C)
C) 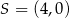 D)
D) 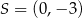
Wszystkie wierzchołki kwadratu 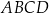 mają współrzędne nieujemne, przy czym
mają współrzędne nieujemne, przy czym 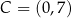 i
i 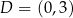 . Okrąg wpisany w kwadrat
. Okrąg wpisany w kwadrat 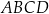 jest określony równaniem
jest określony równaniem
A) 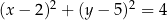 B)
B) 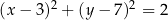
C) 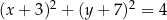 D)
D) 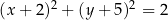
Dany jest trójkąt równoboczny 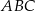 o boku długości 8. Ze środka
o boku długości 8. Ze środka 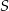 boku
boku 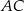 zakreślono koło o promieniu równym połowie boku trójkąta (zobacz rysunek).
zakreślono koło o promieniu równym połowie boku trójkąta (zobacz rysunek).
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Krótsze z łuków wyciętych przez punkty 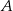 i i 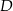 , oraz , oraz 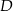 i i 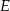 z danego okręgu, mają tą samą długość. z danego okręgu, mają tą samą długość. | P | F |
Odcinek 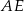 jest dwa razy dłuższy od odcinka jest dwa razy dłuższy od odcinka 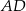 . . | P | F |
Podstawą graniastosłupa prostego jest romb, w którym miara kąta ostrego jest równa 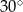 . Każda krawędź tego graniastosłupa ma długość równą 2 (zobacz rysunek).
. Każda krawędź tego graniastosłupa ma długość równą 2 (zobacz rysunek).
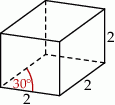
Pole powierzchni całkowitej tego graniastosłupa jest równe
A) 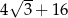 B)
B) 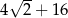 C) 18 D) 20
C) 18 D) 20
Odcinki 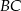 i
i 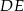 są równoległe i
są równoległe i 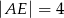 ,
, 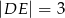 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 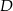 jest środkiem odcinka
jest środkiem odcinka 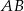 . Długość odcinka
. Długość odcinka 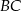 jest równa
jest równa
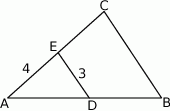
A) 4 B) 6 C) 8 D) 16
Odcinki 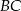 i
i 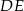 są równoległe i
są równoległe i 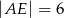 ,
, 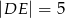 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 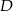 jest środkiem odcinka
jest środkiem odcinka 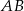 . Długość odcinka
. Długość odcinka 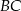 jest równa
jest równa
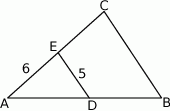
A) 10 B) 6 C) 8 D) 30
W prostopadłościanie 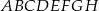 mamy:
mamy: 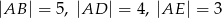 . Który z odcinków
. Który z odcinków 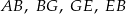 jest najdłuższy?
jest najdłuższy?
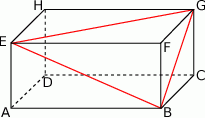
A) 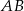 B)
B) 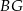 C)
C) 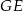 D)
D) 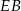
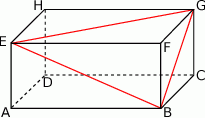
W prostopadłościanie 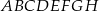 mamy:
mamy: 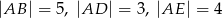 . Który z odcinków
. Który z odcinków 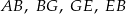 jest najdłuższy?
jest najdłuższy?
A) 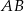 B)
B) 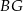 C)
C) 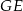 D)
D) 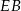
W każdym  –kącie wypukłym (
–kącie wypukłym (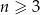 ) liczba przekątnych jest równa
) liczba przekątnych jest równa 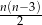 . Wielokątem wypukłym, w którym liczba przekątnych jest o 25 większa od liczby boków, jest
. Wielokątem wypukłym, w którym liczba przekątnych jest o 25 większa od liczby boków, jest
A) siedmiokąt. B) dziesięciokąt. C) dwunastokąt. D) piętnastokąt.
W każdym  –kącie wypukłym (
–kącie wypukłym (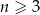 ) liczba przekątnych jest równa
) liczba przekątnych jest równa 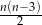 . Wielokątem wypukłym, w którym liczba przekątnych jest o 33 większa od liczby boków, jest
. Wielokątem wypukłym, w którym liczba przekątnych jest o 33 większa od liczby boków, jest
A) dziewięciokąt. B) jedenastokąt. C) dziesięciokąt. D) piętnastokąt.
