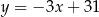W trapezie 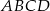 , w którym
, w którym 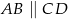 , przedłużono ramiona
, przedłużono ramiona 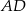 i
i 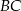 do przecięcia się w punkcie
do przecięcia się w punkcie 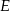 . Wiadomo, że
. Wiadomo, że 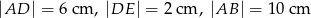 . Wobec tego odcinek
. Wobec tego odcinek 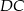 ma długość
ma długość
A) 2,5 cm B) 2 cm C) 3 cm D) 3,5 cm
/Szkoła średnia/Zadania testowe/Geometria
W trapezie 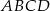 , w którym
, w którym 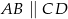 , przedłużono ramiona
, przedłużono ramiona 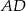 i
i 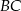 do przecięcia się w punkcie
do przecięcia się w punkcie 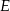 . Wiadomo, że
. Wiadomo, że 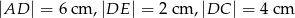 . Wobec tego odcinek
. Wobec tego odcinek 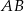 ma długość
ma długość
A) 15,5 cm B) 15 cm C) 16 cm D) 16,5 cm
W trapezie 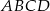 , w którym
, w którym 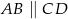 , przedłużono ramiona
, przedłużono ramiona 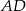 i
i 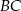 do przecięcia się w punkcie
do przecięcia się w punkcie 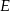 . Wiadomo, że
. Wiadomo, że 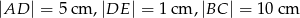 . Wobec tego odcinek
. Wobec tego odcinek 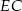 ma długość
ma długość
A) 2,5 cm B) 2 cm C) 3 cm D) 3,5 cm
Proste o równaniach 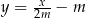 i
i 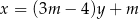 są równoległe, gdy
są równoległe, gdy
A) 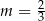 B)
B) 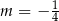 C)
C) 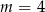 D)
D) 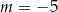
W układzie współrzędnych dany jest okrąg  opisany równaniem
opisany równaniem 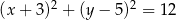 . Pole trójkąta równobocznego wpisanego w ten okrąg jest równe
. Pole trójkąta równobocznego wpisanego w ten okrąg jest równe
A) 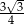 B) 6 C)
B) 6 C) 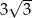 D)
D) 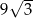
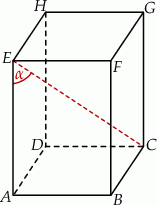
Podstawą graniastosłupa prostego czworokątnego 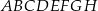 jest kwadrat
jest kwadrat 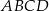 o polu 4 (zobacz rysunek). Objętość graniastosłupa jest równa
o polu 4 (zobacz rysunek). Objętość graniastosłupa jest równa 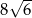 . Miara kąta
. Miara kąta 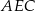 jest równa
jest równa
A) 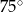 B)
B) 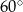 C)
C) 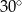 D)
D) 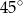
Odległość punktu 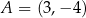 od jego obrazu w symetrii względem początku układu współrzędnych jest równa
od jego obrazu w symetrii względem początku układu współrzędnych jest równa
A) 6 B) 7 C) 8 D) 10
Punkt 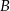 jest obrazem punktu
jest obrazem punktu 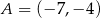 w symetrii względem początku układu współrzędnych. Długość odcinka
w symetrii względem początku układu współrzędnych. Długość odcinka 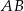 jest równa
jest równa
A) 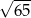 B)
B) 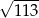 C)
C) 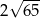 D) 13
D) 13
Punkt 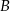 jest obrazem punktu
jest obrazem punktu 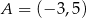 w symetrii względem początku układu współrzędnych. Długość odcinka
w symetrii względem początku układu współrzędnych. Długość odcinka 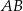 jest równa
jest równa
A) 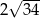 B) 8 C)
B) 8 C) 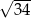 D) 12
D) 12
Objętość walca, w którym wysokość jest trzykrotnie dłuższa od promienia podstawy, jest równa 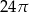 . Zatem promień podstawy tego walca jest ma długość:
. Zatem promień podstawy tego walca jest ma długość:
A) 4 B) 8 C) 2 D) 6
Dany jest walec, w którym wysokość jest równa promieniowi podstawy. Objętość tego walca jest równa 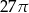 . Wynika stąd, że promień podstawy tego walca jest równy
. Wynika stąd, że promień podstawy tego walca jest równy
A) 9 B) 6 C) 3 D) 2
Objętość walca, w którym wysokość jest trzykrotnie krótsza od promienia podstawy, jest równa 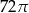 . Zatem promień podstawy tego walca ma długość:
. Zatem promień podstawy tego walca ma długość:
A) 4 B) 8 C) 2 D) 6
Średnicą okręgu jest odcinek 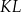 , gdzie
, gdzie 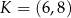 i
i 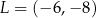 . Równanie tego okręgu ma postać
. Równanie tego okręgu ma postać
A) 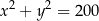 B)
B) 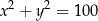 C)
C) 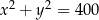 D)
D) 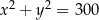
W kartezjańskim układzie współrzędnych 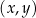 odcinek o końcach
odcinek o końcach 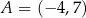 oraz
oraz 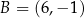 jest średnicą okręgu
jest średnicą okręgu 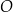 . Okrąg
. Okrąg 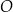 jest określony równaniem
jest określony równaniem
A) 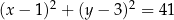 B)
B) 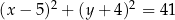
C) 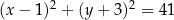 D)
D) 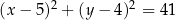
Kąt  jest kątem ostrym w trójkącie prostokątnym i
jest kątem ostrym w trójkącie prostokątnym i 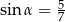 . Wówczas
. Wówczas
A) 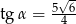 B)
B) 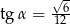 C)
C) 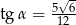 D)
D) 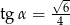
Pole powierzchni bocznej stożka wynosi 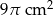 . Tworząca stożka jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego stożka jest równe
. Tworząca stożka jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego stożka jest równe
A) 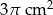 B)
B) 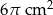 C)
C) 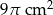 D)
D) 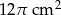
W graniastosłupie prawidłowym czworokątnym 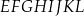 wierzchołki
wierzchołki 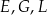 połączono odcinkami (tak jak na rysunku).
połączono odcinkami (tak jak na rysunku).
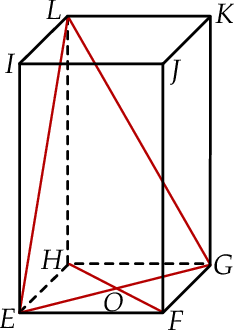
Wskaż kąt między wysokością 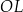 trójkąta
trójkąta 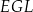 i płaszczyzną podstawy tego graniastosłupa.
i płaszczyzną podstawy tego graniastosłupa.
A) 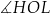 B)
B) 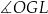 C)
C) 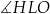 D)
D) 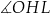
W graniastosłupie prawidłowym czworokątnym 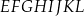 wierzchołki
wierzchołki 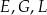 połączono odcinkami (tak jak na rysunku).
połączono odcinkami (tak jak na rysunku).
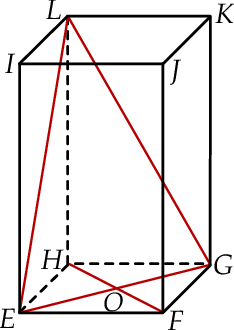
Wskaż kąt między wysokością 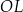 trójkąta
trójkąta 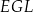 i krawędzią boczną tego graniastosłupa.
i krawędzią boczną tego graniastosłupa.
A) 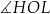 B)
B) 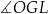 C)
C) 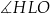 D)
D) 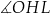
Prosta o równaniu 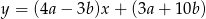 przecina oś
przecina oś 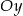 w punkcie
w punkcie 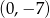 . Wtedy
. Wtedy
A) 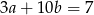 B)
B) 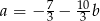 C)
C) 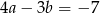 D)
D) 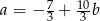
Punkty 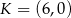 ,
, 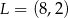 i
i 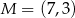 to środki boków, odpowiednio
to środki boków, odpowiednio 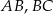 i
i 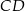 równoległoboku
równoległoboku 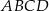 . Różnica długości przekątnych tego równoległoboku jest równa
. Różnica długości przekątnych tego równoległoboku jest równa
A) 4 B) 2 C) 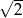 D)
D) 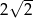
Punkty 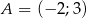 ,
, 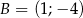 ,
, 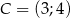 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 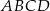 . Równanie prostej zawierającej bok
. Równanie prostej zawierającej bok 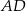 tego równoległoboku ma postać
tego równoległoboku ma postać
A) 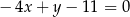 B)
B) 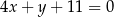
C) 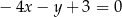 D)
D) 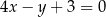
W kartezjańskim układzie współrzędnych 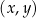 dane są cztery okręgi:
dane są cztery okręgi: 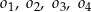 , o równaniach:
, o równaniach:
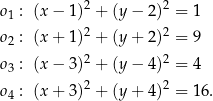
Okręgiem, który nie ma żadnego punktu wspólnego z osiami układu współrzędnych 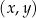 , jest
, jest
A) 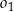 B)
B) 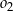 C)
C) 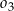 D)
D) 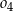
Podstawą graniastosłupa prawidłowego czworokątnego jest kwadrat o boku długości 4, a przekątna ściany bocznej ma długość 5 (zobacz rysunek). Kąt, jaki tworzą przekątna ściany bocznej i przekątna podstawy wychodzące z jednego wierzchołka, ma miarę  .
.
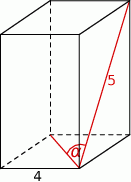
Wtedy wartość 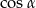 jest równa
jest równa
A)  B)
B) 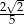 C)
C) 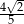 D)
D) 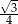
W rombie 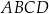 dłuższa przekątna
dłuższa przekątna 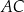 ma długość 12 i tworzy z bokiem
ma długość 12 i tworzy z bokiem 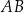 kąt o mierze
kąt o mierze 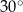 (zobacz rysunek).
(zobacz rysunek).
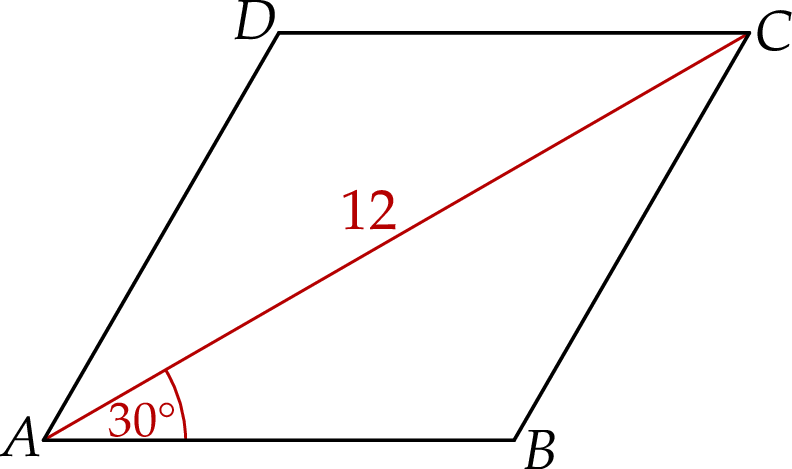
Pole rombu 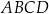 jest równe
jest równe
A) 24 B) 36 C) 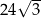 D)
D) 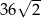
W rombie 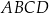 dłuższa przekątna
dłuższa przekątna 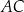 ma długość 8, a kąt rozwarty tego rombu ma miarę
ma długość 8, a kąt rozwarty tego rombu ma miarę 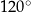 (zobacz rysunek).
(zobacz rysunek).
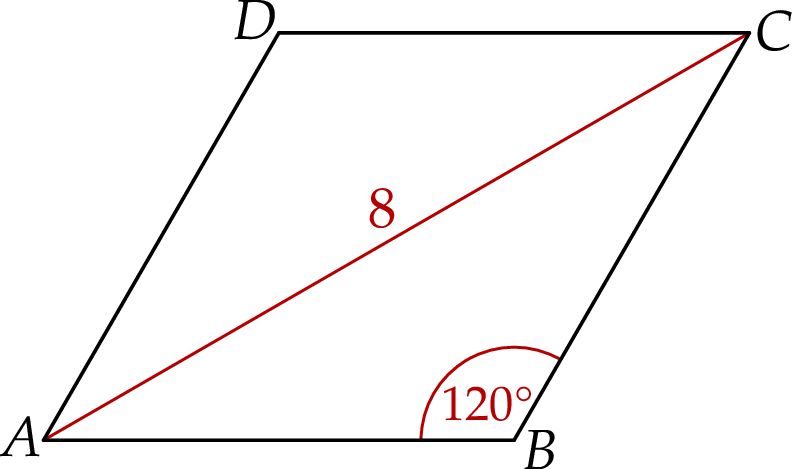
Pole rombu 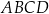 jest równe
jest równe
A) 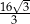 B) 8 C)
B) 8 C) 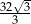 D) 16
D) 16
W trójkącie 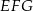 bok
bok 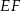 ma długość 21. Prosta równoległa do boku
ma długość 21. Prosta równoległa do boku 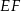 przecina boki
przecina boki 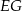 i
i 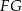 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 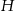 oraz
oraz 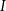 (zobacz rysunek) w taki sposób, że
(zobacz rysunek) w taki sposób, że 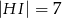 i
i 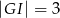 . Wtedy długość odcinka
. Wtedy długość odcinka 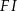 jest równa
jest równa
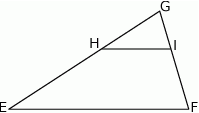
A) 6 B) 9 C) 12 D) 17
W trójkącie 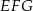 bok
bok 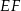 ma długość 24. Prosta równoległa do boku
ma długość 24. Prosta równoległa do boku 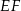 przecina boki
przecina boki 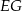 i
i 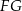 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 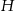 oraz
oraz 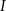 (zobacz rysunek) w taki sposób, że
(zobacz rysunek) w taki sposób, że 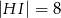 i
i 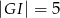 . Wtedy długość odcinka
. Wtedy długość odcinka 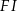 jest równa
jest równa
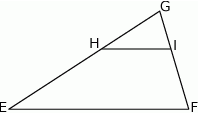
A) 6 B) 9 C) 10 D) 12
Przekątna prostokątna ma długość 6, a długość jego krótszego boku jest równa 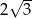 . Kąt rozwarty
. Kąt rozwarty  między przekątnymi tego prostokąta spełnia warunek
między przekątnymi tego prostokąta spełnia warunek
A) 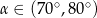 B)
B) 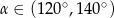 C)
C) 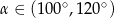 D)
D) 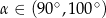
W układzie współrzędnych na płaszczyźnie dany jest punkt 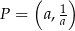 , gdzie
, gdzie  jest pewną liczbą niezerową. Punkt
jest pewną liczbą niezerową. Punkt 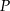 może należeć do tej samej ćwiartki układu współrzędnych, co punkt
może należeć do tej samej ćwiartki układu współrzędnych, co punkt
A) 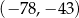 B)
B) 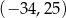 C)
C) 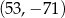 D)
D) 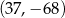
Okrąg o równaniu 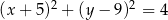 ma środek
ma środek 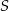 i promień
i promień  . Wówczas
. Wówczas
A) 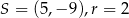 B)
B) 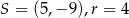
C) 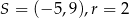 D)
D) 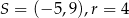
Okrąg o równaniu 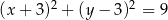 ma środek
ma środek 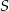 i promień
i promień  . Wówczas
. Wówczas
A) 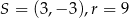 B)
B) 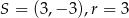
C) 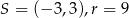 D)
D) 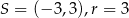
Okrąg o równaniu 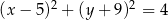 ma środek
ma środek 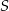 i promień
i promień  . Wówczas
. Wówczas
A) 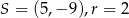 B)
B) 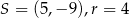
C) 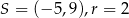 D)
D) 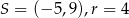
Okrąg o równaniu 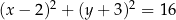 ma środek
ma środek 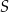 i promień
i promień  . Wówczas
. Wówczas
A) 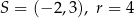 B)
B) 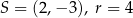
C) 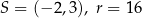 D)
D) 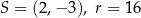
Punkt 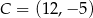 jest wierzchołkiem trójkąta równoramiennego, którego podstawa
jest wierzchołkiem trójkąta równoramiennego, którego podstawa 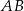 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 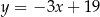 . Wysokość opuszczona na podstawę
. Wysokość opuszczona na podstawę 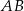 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu
A) 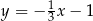 B)
B) 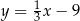 C)
C) 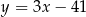 D)
D)