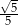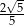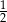W kartezjańskim układzie współrzędnych 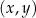 , danych jest 5 prostych o równaniach
, danych jest 5 prostych o równaniach
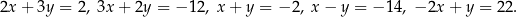
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wśród podanych prostych są proste prostopadłe. | P | F |
| Wszystkie podane proste przecinają się w jednym punkcie. | P | F |

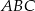 miary kątów wynoszą:
miary kątów wynoszą: 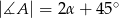 ,
, 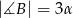 ,
, 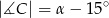 . Wówczas
. Wówczas 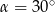
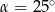
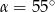
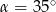
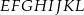 poprowadzono z wierzchołka
poprowadzono z wierzchołka 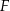 dwie przekątne sąsiednich ścian,
dwie przekątne sąsiednich ścian, 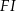 oraz
oraz 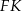 (zobacz rysunek). Miara kąta
(zobacz rysunek). Miara kąta 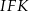 jest równa
jest równa 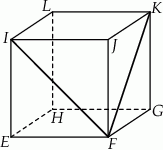
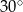
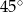
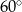
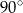
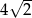 i długości krawędzi przy podstawie równej 4 wynosi
i długości krawędzi przy podstawie równej 4 wynosi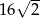
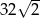
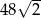
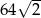
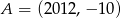 i
i 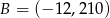 są końcami odcinka
są końcami odcinka 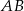 , to środkiem tego odcinka jest punkt o współrzędnych
, to środkiem tego odcinka jest punkt o współrzędnych 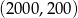
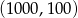
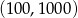
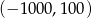
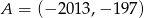 i
i 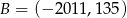 są końcami odcinka
są końcami odcinka 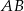 , to środkiem tego odcinka jest punkt o współrzędnych
, to środkiem tego odcinka jest punkt o współrzędnych 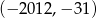
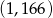
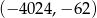
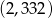
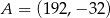 ,
, 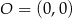 i
i 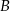 są wierzchołkami trójkąta prostokątnego o przeciwprostokątnej
są wierzchołkami trójkąta prostokątnego o przeciwprostokątnej 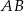 . Wskaż równanie prostej zawierającej przyprostokątną
. Wskaż równanie prostej zawierającej przyprostokątną 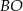 tego trójkąta.
tego trójkąta.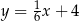
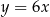
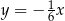
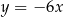
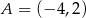 od prostych o równaniach
od prostych o równaniach 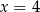 i
i 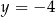 jest równa
jest równa 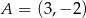 od prostych o równaniach
od prostych o równaniach 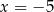 i
i 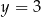 jest równa
jest równa 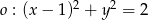 i prosta
i prosta 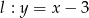 . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe.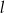 przechodzi przez środek okręgu.
przechodzi przez środek okręgu. 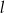 jest rozłączna z okręgiem.
jest rozłączna z okręgiem. 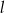 jest styczna do okręgu.
jest styczna do okręgu. 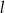 ma z okręgiem dwa punkty wspólne.
ma z okręgiem dwa punkty wspólne. 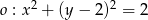 i prosta
i prosta 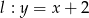 . Wskaż zdanie prawdziwe.
. Wskaż zdanie prawdziwe. jest rozłączna z okręgiem.
jest rozłączna z okręgiem.  przechodzi przez środek okręgu.
przechodzi przez środek okręgu.  jest styczna do okręgu.
jest styczna do okręgu. 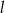 ma z okręgiem jeden punkt wspólny.
ma z okręgiem jeden punkt wspólny.  , takim, że
, takim, że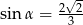
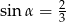
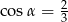
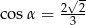
 , takim, że
, takim, że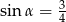
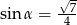
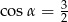
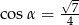
 , takim, że
, takim, że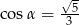
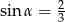
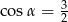
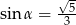
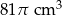 . Wysokość stożka jest 9 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego stożka jest równe
. Wysokość stożka jest 9 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego stożka jest równe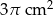
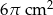
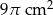
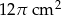
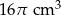 . Wysokość stożka jest 6 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego stożka jest równe
. Wysokość stożka jest 6 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego stożka jest równe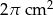
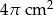
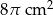
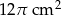
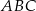 o kącie między ramionami
o kącie między ramionami 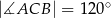 . Punkt
. Punkt 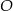 jest środkiem okręgu wpisanego w ten trójkąt. Prosta
jest środkiem okręgu wpisanego w ten trójkąt. Prosta 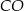 przecina podstawę
przecina podstawę 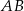 w punkcie
w punkcie 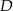 . Miara kąta
. Miara kąta 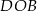 jest równa
jest równa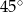
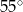
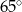
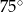
 o kącie między ramionami
o kącie między ramionami 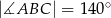 . Punkt
. Punkt 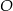 jest środkiem okręgu wpisanego w ten trójkąt. Prosta
jest środkiem okręgu wpisanego w ten trójkąt. Prosta 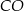 przecina podstawę
przecina podstawę 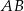 w punkcie
w punkcie 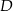 . Miara kąta
. Miara kąta 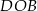 jest równa
jest równa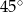
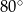
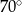
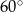
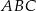 o kącie między ramionami
o kącie między ramionami 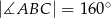 . Punkt
. Punkt 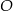 jest środkiem okręgu wpisanego w ten trójkąt. Prosta
jest środkiem okręgu wpisanego w ten trójkąt. Prosta 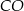 przecina podstawę
przecina podstawę 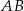 w punkcie
w punkcie 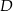 . Miara kąta
. Miara kąta 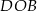 jest równa
jest równa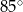
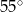
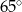
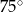
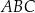 i
i 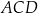 są wpisane w okrąg o środku
są wpisane w okrąg o środku 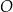 . Odcinek
. Odcinek 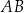 jest średnicą okręgu.
jest średnicą okręgu. 
 zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa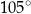
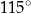
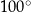
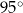
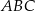 i
i 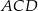 są wpisane w okrąg o środku
są wpisane w okrąg o środku 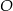 . Odcinek
. Odcinek 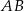 jest średnicą okręgu.
jest średnicą okręgu. 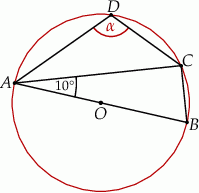
 zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa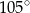
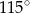
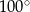
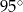
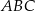 i
i 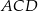 są wpisane w okrąg o środku
są wpisane w okrąg o środku 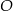 . Odcinek
. Odcinek 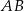 jest średnicą okręgu.
jest średnicą okręgu. 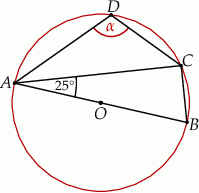
 zaznaczonego na rysunku jest równa
zaznaczonego na rysunku jest równa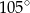
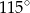
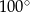
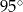
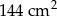 . Jeśli przyjmiemy
. Jeśli przyjmiemy 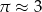 , to promień podstawy walca będzie równy około
, to promień podstawy walca będzie równy około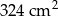 . Jeśli przyjmiemy
. Jeśli przyjmiemy 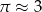 , to promień podstawy walca będzie równy około
, to promień podstawy walca będzie równy około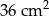 . Jeśli przyjmiemy
. Jeśli przyjmiemy 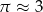 , to promień podstawy walca będzie równy około
, to promień podstawy walca będzie równy około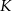 skrócono o 20%, a długość drugiego boku skrócono o 40%. W wyniku tych operacji otrzymano prostokąt
skrócono o 20%, a długość drugiego boku skrócono o 40%. W wyniku tych operacji otrzymano prostokąt 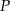 . Stosunek długości przekątnej kwadratu
. Stosunek długości przekątnej kwadratu 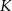 do długości przekątnej prostokąta
do długości przekątnej prostokąta 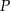 jest równy
jest równy 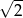
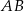 , gdzie
, gdzie 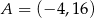 i
i 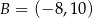 oraz prosta
oraz prosta 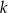 o równaniu
o równaniu 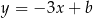 . Jeżeli prosta
. Jeżeli prosta 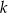 przecina odcinek
przecina odcinek 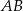 w takim punkcie
w takim punkcie 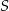 , że
, że 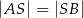 , to liczba
, to liczba 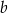 jest równa
jest równa 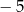
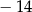
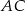 jest średnicą okręgu opisanego na czworokącie
jest średnicą okręgu opisanego na czworokącie 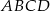 . Punkt przecięcia przekątnych dzieli przekątną
. Punkt przecięcia przekątnych dzieli przekątną 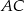 na odcinki o długościach 3 i 6. Zatem długość okręgu opisanego na czworokącie
na odcinki o długościach 3 i 6. Zatem długość okręgu opisanego na czworokącie 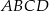 jest równa
jest równa 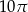
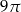
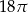
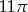
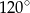
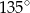
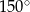
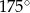
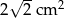 . Zatem przeciwprostokątna ma długość:
. Zatem przeciwprostokątna ma długość: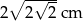
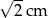
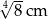
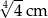
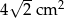 . Zatem przeciwprostokątna ma długość:
. Zatem przeciwprostokątna ma długość: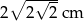
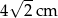
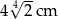
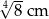
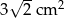 . Zatem przeciwprostokątna ma długość:
. Zatem przeciwprostokątna ma długość: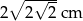
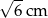
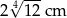
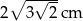
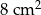 . Przeciwprostokątna tego trójkąta ma długość
. Przeciwprostokątna tego trójkąta ma długość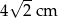
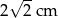
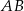 , gdzie
, gdzie 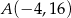 ,
, 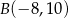 . Punkt
. Punkt  jest środkiem odcinka
jest środkiem odcinka 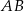 . Obrazem punktu
. Obrazem punktu 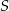 w symetrii względem osi
w symetrii względem osi 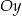 jest punkt
jest punkt 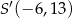
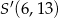
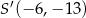
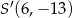
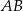 , gdzie
, gdzie 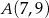 ,
, 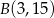 . Punkt
. Punkt 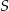 jest środkiem odcinka
jest środkiem odcinka 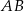 . Obrazem punktu
. Obrazem punktu 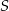 w symetrii względem osi
w symetrii względem osi 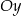 jest punkt
jest punkt 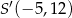
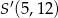
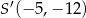
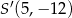
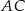 trójkąta prostokątnego
trójkąta prostokątnego 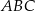 ma długość 6, a przeciwprostokątna
ma długość 6, a przeciwprostokątna 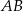 ma długość
ma długość 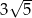 . Wtedy tangens kąta ostrego
. Wtedy tangens kąta ostrego 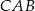 tego trójkąta jest równy
tego trójkąta jest równy