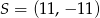W trójkącie prostokątnym o przyprostokątnych długości 4 i 5 połączono wierzchołek 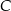 kąta prostego ze środkiem
kąta prostego ze środkiem 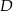 przeciwprostokątnej. Długość odcinka
przeciwprostokątnej. Długość odcinka 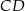 jest równa
jest równa
A) 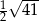 B) 4,5 C) 4 D)
B) 4,5 C) 4 D) 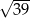
/Szkoła średnia/Zadania testowe/Geometria
W trójkącie prostokątnym o przyprostokątnych długości 6 i 8 połączono wierzchołek 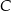 kąta prostego ze środkiem
kąta prostego ze środkiem 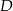 przeciwprostokątnej. Długość odcinka
przeciwprostokątnej. Długość odcinka 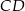 jest równa
jest równa
A) 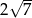 B) 10 C) 7 D) 5
B) 10 C) 7 D) 5
W trójkącie prostokątnym o przyprostokątnych długości 5 i 12 połączono wierzchołek 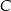 kąta prostego ze środkiem
kąta prostego ze środkiem 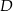 przeciwprostokątnej. Długość odcinka
przeciwprostokątnej. Długość odcinka 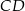 jest równa
jest równa
A) 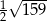 B) 6,5 C) 13 D)
B) 6,5 C) 13 D) 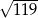
Długości boków trójkąta prostokątnego wynoszą 8 cm, 15 cm, 17 cm. Odcinek łączący środek przeciwprostokątnej z wierzchołkiem kąta prostego tego trójkąta ma długość
A) 8 cm B) 7,5 cm C) 9 cm D) 8,5 cm
W trójkącie prostokątnym o przyprostokątnych długości 7 i 24 połączono wierzchołek 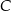 kąta prostego ze środkiem
kąta prostego ze środkiem 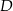 przeciwprostokątnej. Długość odcinka
przeciwprostokątnej. Długość odcinka 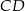 jest równa
jest równa
A) 25 B) 12 C) 15 D) 12,5
Styczną do okręgu 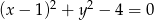 jest prosta o równaniu
jest prosta o równaniu
A) 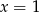 B)
B) 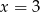 C)
C) 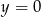 D)
D) 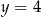
Styczną do okręgu 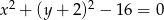 jest prosta o równaniu
jest prosta o równaniu
A) 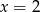 B)
B) 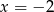 C)
C) 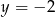 D)
D) 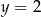
Wskaż równanie prostej, której fragment przedstawiony jest na poniższym wykresie
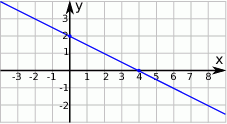
A) 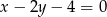 B)
B) 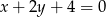 C)
C) 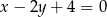 D)
D) 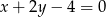
Wskaż równanie prostej, której fragment przedstawiony jest na poniższym wykresie
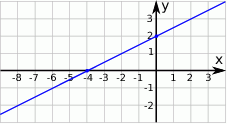
A) 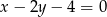 B)
B) 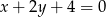 C)
C) 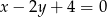 D)
D) 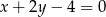
Pole trójkąta prostokątnego 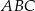 , przedstawionego na rysunku, jest równe
, przedstawionego na rysunku, jest równe
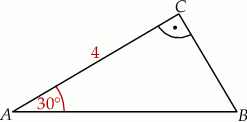
A) 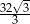 B)
B) 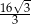 C)
C) 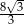 D)
D) 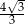
Pole trójkąta prostokątnego 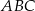 , przedstawionego na rysunku, jest równe
, przedstawionego na rysunku, jest równe
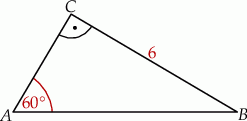
A) 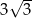 B)
B) 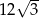 C)
C) 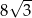 D)
D) 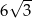
Na boku 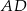 kwadratu
kwadratu 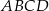 zbudowano trójkąt równoboczny
zbudowano trójkąt równoboczny 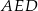 . Punkt
. Punkt 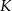 jest środkiem odcinka
jest środkiem odcinka 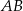 , a punkt
, a punkt 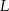 środkiem odcinka
środkiem odcinka 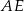 .
.
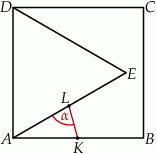
Miara kąta  jest równa
jest równa
A) 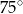 B)
B) 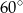 C)
C) 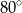 D)
D) 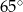
Dane są punkty 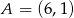 i
i 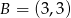 . Współczynnik kierunkowy prostej
. Współczynnik kierunkowy prostej 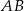 jest równy
jest równy
A) 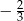 B)
B) 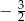 C)
C)  D)
D) 
W kartezjańskim układzie współrzędnych 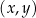 prosta o równaniu
prosta o równaniu 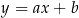 przechodzi przez punkty
przechodzi przez punkty 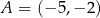 oraz
oraz 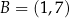 . Współczynnik
. Współczynnik  w równaniu tej prostej jest równy
w równaniu tej prostej jest równy
A)  B)
B) 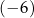 C)
C)  D)
D) 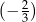
W kartezjańskim układzie współrzędnych 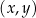 prosta o równaniu
prosta o równaniu 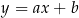 przechodzi przez punkty
przechodzi przez punkty 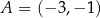 oraz
oraz 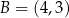 . Współczynnik
. Współczynnik  w równaniu tej prostej jest równy
w równaniu tej prostej jest równy
A) 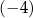 B)
B) 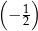 C) 2 D)
C) 2 D) 
Wiadomo, że punkty 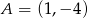 i
i 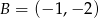 należą do prostej
należą do prostej 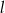 . Wówczas współczynnik kierunkowy prostej
. Wówczas współczynnik kierunkowy prostej 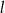 jest równy
jest równy
A) 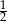 B) 1 C)
B) 1 C) 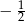 D)
D) 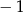
Współczynnik kierunkowy prostej, na której leżą punkty 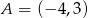 oraz
oraz 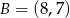 , jest równy
, jest równy
A) 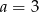 B)
B) 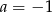 C)
C) 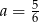 D)
D) 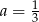
W układzie współrzędnych dane są dwa punkty 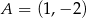 oraz
oraz 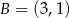 . Współczynnik kierunkowy prostej
. Współczynnik kierunkowy prostej 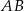 jest równy
jest równy
A) 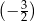 B)
B) 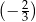 C)
C) 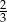 D)
D) 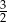
W układzie współrzędnych dane są dwa punkty 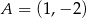 oraz
oraz 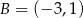 . Współczynnik kierunkowy prostej
. Współczynnik kierunkowy prostej 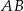 jest równy
jest równy
A) 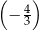 B)
B) 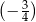 C)
C) 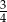 D)
D) 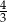
Współczynnik kierunkowy prostej, na której leżą punkty 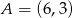 oraz
oraz 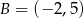 , jest równy
, jest równy
A) 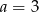 B)
B) 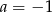 C)
C) 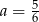 D)
D) 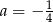
Punkty 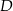 ,
, 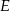 i
i 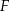 są punktami styczności okręgu wpisanego w trójkąt
są punktami styczności okręgu wpisanego w trójkąt 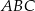 z jego bokami i
z jego bokami i 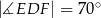 (zobacz rysunek).
(zobacz rysunek).
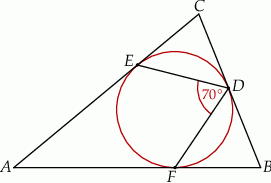
Miara kąta 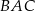 jest równa
jest równa
A) 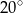 B)
B) 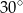 C)
C) 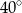 D)
D) 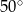
Odległość środka okręgu od prostej jest równa 0. Zatem liczba punktów wspólnych okręgu i prostej jest równa
A) 0 B) 1 C) 2 D) 3
Odległość środka okręgu o średnicy 14 od prostej jest równa 7. Zatem liczba punktów wspólnych okręgu i prostej jest równa:
A) 0 B) 1 C) 2 D) 3
Podstawą ostrosłupa jest kwadrat 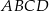 o boku długości 4. Krawędź boczna
o boku długości 4. Krawędź boczna 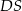 jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
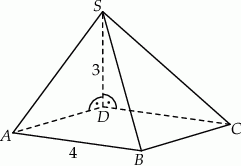
Pole ściany 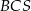 tego ostrosłupa jest równe
tego ostrosłupa jest równe
A) 20 B) 10 C) 16 D) 12
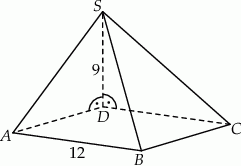
Podstawą ostrosłupa jest kwadrat 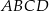 o boku długości 12. Krawędź boczna
o boku długości 12. Krawędź boczna 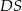 jest prostopadła do podstawy i ma długość 9 (zobacz rysunek).
jest prostopadła do podstawy i ma długość 9 (zobacz rysunek).
Pole ściany 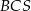 tego ostrosłupa jest równe
tego ostrosłupa jest równe
A) 180 B) 108 C) 54 D) 90
Iloczyn długości wszystkich krawędzi sześcianu jest równy 16. Objętość tego sześcianu jest równa
A) 12 B) 2 C) 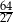 D)
D) 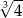
Przekątna prostokąta ma długość 12 cm i tworzy z jednym z boków kąt o mierze 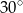 . Pole powierzchni tego prostokąta jest równe
. Pole powierzchni tego prostokąta jest równe
A) 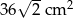 B)
B) 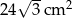 C)
C) 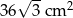 D)
D) 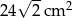
Stosunek pól kół wpisanego i opisanego na kwadracie o boku długości  jest równy:
jest równy:
A) 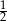 B)
B) 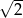 C)
C) 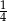 D)
D) 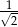
Stosunek pola koła wpisanego w kwadrat do pola koła opisanego na tym kwadracie jest równy:
A) 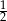 B)
B) 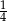 C)
C) 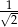 D)
D) 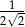
Stosunek pola kwadratu wpisanego w okrąg do pola kwadratu opisanego na tym okręgu wynosi
A) 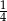 B)
B) 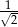 C)
C) 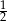 D)
D) 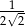
Tangens kąta  zaznaczonego na rysunku jest równy
zaznaczonego na rysunku jest równy
A) 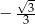 B)
B) 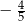 C)
C) 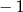 D)
D) 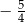
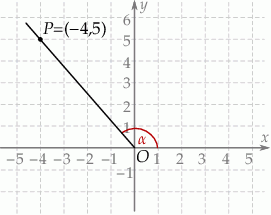
W kartezjańskim układzie współrzędnych 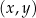 zaznaczono kąt
zaznaczono kąt  o wierzchołku w punkcie
o wierzchołku w punkcie 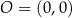 . Jedno z ramion tego kąta pokrywa się z dodatnią półosią
. Jedno z ramion tego kąta pokrywa się z dodatnią półosią 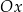 , a drugie przechodzi przez punkt
, a drugie przechodzi przez punkt 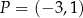 (zobacz rysunek).
(zobacz rysunek).
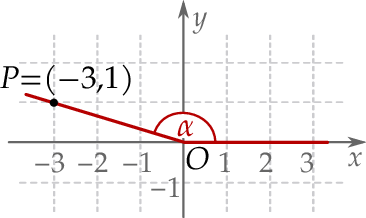
Tangens kąta  jest równy
jest równy
A) 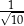 B)
B) 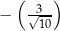 C)
C) 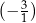 D)
D) 
Na rysunku przedstawiona jest prosta 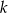 , przechodząca przez punkt
, przechodząca przez punkt 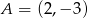 i przez początek układu współrzędnych, oraz zaznaczony jest kąt
i przez początek układu współrzędnych, oraz zaznaczony jest kąt  nachylenia tej prostej do osi
nachylenia tej prostej do osi 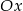 .
.
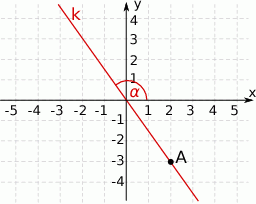
Zatem
A) 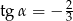 B)
B) 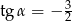 C)
C) 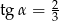 D)
D) 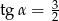
Tangens kąta  zaznaczonego na rysunku jest równy
zaznaczonego na rysunku jest równy
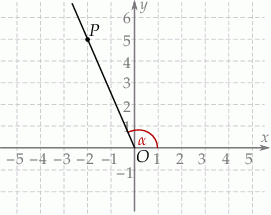
A) 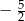 B)
B)  C)
C) 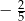 D)
D) 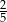
Tangens kąta  zaznaczonego na rysunku jest równy
zaznaczonego na rysunku jest równy
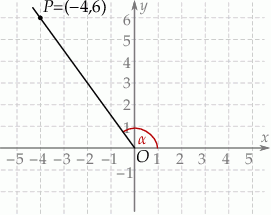
A) 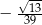 B)
B) 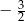 C)
C) 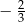 D)
D) 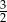
Na rysunku przedstawiona jest prosta, przechodząca przez punkty 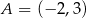 i
i 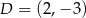 , oraz zaznaczony jest kąt
, oraz zaznaczony jest kąt  nachylenia tej prostej do osi
nachylenia tej prostej do osi 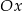 .
.
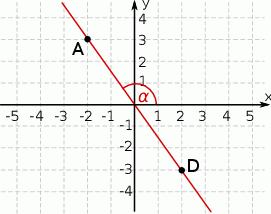
Zatem tangens kąta  jest równy
jest równy
A)  B)
B) 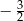 C)
C)  D)
D) 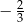
Na rysunku przedstawiona jest prosta 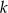 , przechodząca przez punkt
, przechodząca przez punkt 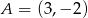 i przez początek układu współrzędnych, oraz zaznaczony jest kąt
i przez początek układu współrzędnych, oraz zaznaczony jest kąt  nachylenia tej prostej do osi
nachylenia tej prostej do osi 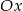 .
.
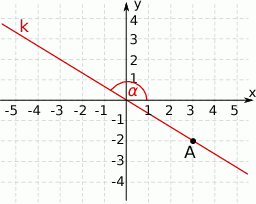
Zatem
A) 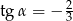 B)
B) 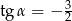 C)
C) 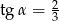 D)
D) 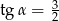
W kartezjańskim układzie współrzędnych 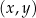 zaznaczono kąt
zaznaczono kąt  o wierzchołku w punkcie
o wierzchołku w punkcie 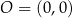 . Jedno z ramion tego kąta pokrywa się z dodatnią półosią
. Jedno z ramion tego kąta pokrywa się z dodatnią półosią 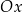 , a drugie przechodzi przez punkt
, a drugie przechodzi przez punkt 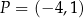 (zobacz rysunek).
(zobacz rysunek).
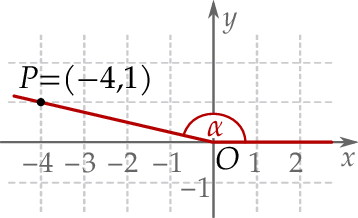
Tangens kąta  jest równy
jest równy
A) 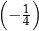 B)
B) 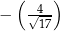 C)
C) 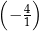 D)
D) 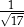
Graniastosłup o podstawie ośmiokąta ma dokładnie
A) 16 wierzchołków. B) 9 wierzchołków. C) 16 krawędzi. D) 8 krawędzi.
Graniastosłup o podstawie dziewięciokąta ma dokładnie
A) 16 wierzchołków. B) 18 wierzchołków. C) 24 krawędzie. D) 18 krawędzi.
Prosta 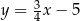 jest osią symetrii trójkąta
jest osią symetrii trójkąta 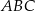 , w którym
, w którym 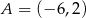 i
i 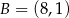 . Bok
. Bok 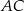 tego trójkąta jest zawarty w prostej o równaniu
tego trójkąta jest zawarty w prostej o równaniu
A) 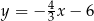 B)
B) 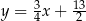 C)
C) 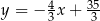 D)
D) 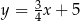
Sinus kąta ostrego równoległoboku jest równy  . Suma cosinusów wszystkich kątów wewnętrznych tego równoległoboku jest równa
. Suma cosinusów wszystkich kątów wewnętrznych tego równoległoboku jest równa
A) 0 B) 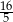 C)
C) 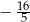 D)
D) 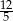
Przyprostokątne trójkąta prostokątnego mają długości 1 i 7. Sinus najmniejszego kąta tego trójkąta jest równy
A) 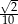 B)
B) 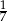 C)
C) 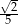 D)
D) 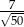
Przyprostokątne trójkąta prostokątnego mają długości 2 i 6. Sinus najmniejszego kąta tego trójkąta jest równy
A) 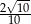 B)
B) 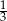 C)
C) 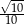 D)
D) 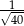
Przyprostokątne trójkąta prostokątnego mają długości 8 i 6. Sinus większego z kątów ostrych tego trójkąta jest równy
A)  B)
B)  C)
C)  D)
D) 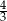
Przyprostokątne trójkąta prostokątnego mają długości 3 i 9. Sinus najmniejszego kąta tego trójkąta jest równy
A) 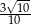 B)
B) 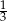 C)
C) 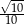 D)
D) 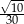
Przyprostokątne w trójkącie prostokątnym mają długości 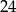 i
i 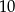 . Sinus najmniejszego kąta jest równy
. Sinus najmniejszego kąta jest równy
A) 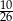 B)
B) 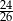 C)
C) 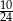 D)
D) 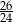
W trójkącie prostokątnym o długościach przyprostokątnych 2 i 5 cosinus większego z kątów ostrych jest równy
A)  B)
B)  C)
C) 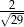 D)
D) 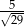
Prosta 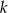 oraz prosta o równaniu
oraz prosta o równaniu 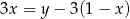 są prostopadłe oraz przecinają się w punkcie
są prostopadłe oraz przecinają się w punkcie 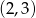 . Prosta
. Prosta 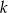 ma równanie
ma równanie
A) 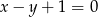 B)
B) 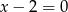 C)
C) 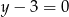 D)
D) 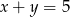
Prosta 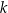 oraz prosta o równaniu
oraz prosta o równaniu 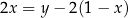 są prostopadłe oraz przecinają się w punkcie
są prostopadłe oraz przecinają się w punkcie 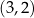 . Prosta
. Prosta 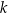 ma równanie
ma równanie
A) 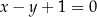 B)
B) 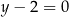 C)
C) 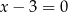 D)
D) 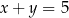
Dane są punkty 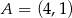 ,
, 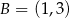 ,
, 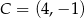 . Pole trójkąta
. Pole trójkąta 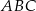 jest równe
jest równe
A) 3 B) 6 C) 8 D) 16
Dane są punkty 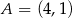 ,
, 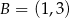 ,
, 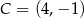 . Pole trójkąta
. Pole trójkąta 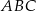 jest równe
jest równe
A) 2 B) 3 C) 6 D) 12
Punkty 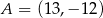 i
i 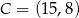 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 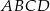 . Przekątne tego kwadratu przecinają się w punkcie
. Przekątne tego kwadratu przecinają się w punkcie
A) 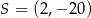 B)
B) 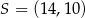 C)
C) 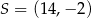 D)
D) 
Punkty 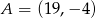 i
i 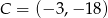 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 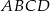 . Przekątne tego kwadratu przecinają się w punkcie
. Przekątne tego kwadratu przecinają się w punkcie
A) 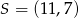 B)
B) 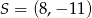 C)
C) 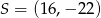 D)
D)