Przekątna sześcianu ma długość 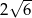 . Suma długości wszystkich krawędzi tego sześcianu wynosi
. Suma długości wszystkich krawędzi tego sześcianu wynosi
A) 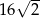 B)
B) 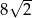 C)
C) 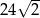 D) 48
D) 48
/Szkoła średnia/Zadania testowe/Geometria
Powierzchnia boczna stożka o promieniu podstawy 6 cm, po rozwinięciu jest wycinkiem koła o kącie 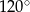 . Pole powierzchni bocznej tego stożka jest równe
. Pole powierzchni bocznej tego stożka jest równe
A) 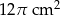 B)
B) 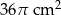 C)
C) 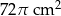 D)
D) 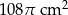
Dany jest prostopadłościan o wymiarach 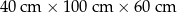 . Jeżeli każdą z najdłuższych krawędzi tego prostopadłościanu wydłużymy o 30%, a każdą z najkrótszych krawędzi skrócimy o 20%, to w wyniku obu tych przekształceń objętość tego prostopadłościanu
. Jeżeli każdą z najdłuższych krawędzi tego prostopadłościanu wydłużymy o 30%, a każdą z najkrótszych krawędzi skrócimy o 20%, to w wyniku obu tych przekształceń objętość tego prostopadłościanu
A) zwiększy się o 8% B) zwiększy się o 4%
C) zmniejszy się o 8% D) zmniejszy się o 4%
Większa część odcinka podzielonego na dwie części w stosunku 3:5 wynosi 20 cm. Długość tego odcinka wynosi:
A) 32 cm B) 27 cm C) 33 cm D) 30 cm
W kwadracie 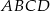 połączono środki boków otrzymując kwadrat
połączono środki boków otrzymując kwadrat 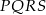 .
.
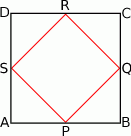
Kwadrat 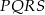 jest podobny do kwadratu
jest podobny do kwadratu 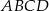 w skali
w skali
A) 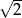 B) 2 C)
B) 2 C) 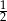 D)
D) 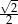
W kwadracie 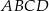 połączono środki boków otrzymując kwadrat
połączono środki boków otrzymując kwadrat 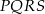 .
.
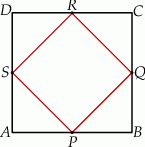
Kwadrat 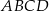 jest podobny do kwadratu
jest podobny do kwadratu 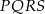 w skali
w skali
A) 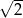 B) 2 C)
B) 2 C) 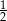 D)
D) 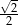
Punkt 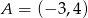 jest początkiem odcinka
jest początkiem odcinka 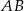 , gdzie
, gdzie 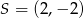 jest jego środkiem. Punkt
jest jego środkiem. Punkt 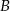 , który jest końcem tego odcinka ma współrzędne
, który jest końcem tego odcinka ma współrzędne
A) 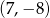 B)
B) 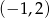 C)
C) 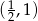 D)
D) 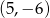
Punkt 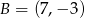 jest końcem odcinka
jest końcem odcinka 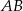 , gdzie
, gdzie 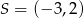 jest jego środkiem. Punkt
jest jego środkiem. Punkt 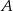 , który jest początkiem tego odcinka ma współrzędne
, który jest początkiem tego odcinka ma współrzędne
A) 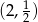 B)
B) 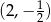 C)
C) 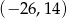 D)
D) 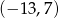
Punkt 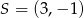 jest środkiem odcinka
jest środkiem odcinka 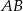 i
i 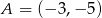 . Punkt
. Punkt 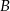 ma współrzędne
ma współrzędne
A) 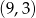 B)
B) 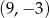 C)
C) 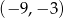 D)
D) 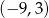
Punkt 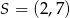 jest środkiem odcinka
jest środkiem odcinka 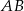 , w którym
, w którym 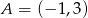 . Punkt
. Punkt 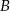 ma współrzędne:
ma współrzędne:
A) 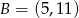 B)
B) 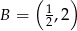 C)
C) 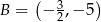 D)
D) 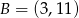
Punkt 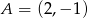 jest początkiem odcinka
jest początkiem odcinka 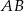 , gdzie
, gdzie 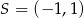 jest jego środkiem. Punkt
jest jego środkiem. Punkt 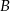 , który jest końcem tego odcinka ma współrzędne
, który jest końcem tego odcinka ma współrzędne
A) 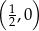 B)
B) 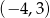 C)
C) 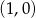 D)
D) 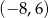
W układzie współrzędnych punkt 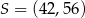 jest środkiem odcinka
jest środkiem odcinka 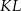 , którego jednym z końców jest punkt
, którego jednym z końców jest punkt 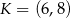 . Zatem
. Zatem
A) 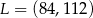 B)
B) 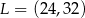 C)
C) 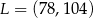 D)
D) 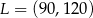
Punkt 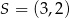 jest środkiem odcinka
jest środkiem odcinka 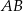 , w którym
, w którym 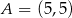 . Punkt
. Punkt 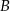 ma współrzędne
ma współrzędne
A) 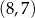 B)
B) 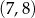 C)
C) 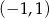 D)
D) 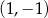
Punkt 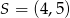 jest środkiem odcinka
jest środkiem odcinka 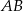 , w którym
, w którym 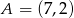 . Punkt
. Punkt 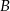 ma współrzędne:
ma współrzędne:
A) 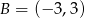 B)
B) 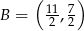 C)
C) 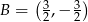 D)
D) 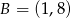
Punkt 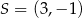 jest środkiem odcinka
jest środkiem odcinka 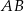 , w którym
, w którym 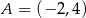 . Punkt
. Punkt 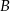 ma współrzędne
ma współrzędne
A) 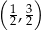 B)
B) 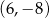 C)
C) 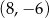 D)
D) 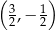
Punkt 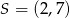 jest środkiem odcinka
jest środkiem odcinka 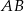 , w którym
, w którym 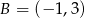 . Punkt
. Punkt 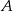 ma współrzędne:
ma współrzędne:
A) 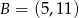 B)
B) 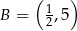 C)
C) 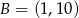 D)
D) 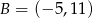
W układzie współrzędnych punkt 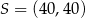 jest środkiem odcinka
jest środkiem odcinka 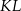 , którego jednym z końców jest punkt
, którego jednym z końców jest punkt 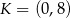 . Zatem
. Zatem
A) 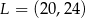 B)
B) 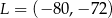 C)
C) 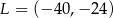 D)
D) 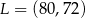
Punkt 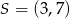 jest środkiem odcinka
jest środkiem odcinka 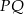 , gdzie
, gdzie 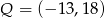 . Zatem punkt
. Zatem punkt 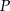 ma współrzędne
ma współrzędne
A) 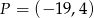 B)
B) 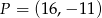 C)
C) 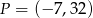 D)
D) 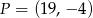
W układzie współrzędnych zaznaczono dwa punkty: 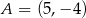 i
i 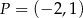 . Punkt
. Punkt 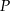 jest środkiem odcinka
jest środkiem odcinka 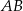 . Jakie współrzędne ma punkt B?
. Jakie współrzędne ma punkt B?
A) 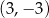 B)
B) 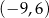 C)
C) 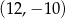 D)
D) 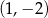
Dane są punkty 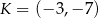 oraz
oraz 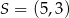 . Punkt
. Punkt 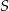 jest środkiem odcinka
jest środkiem odcinka 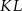 . Wtedy punkt
. Wtedy punkt 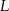 ma współrzędne
ma współrzędne
A) 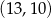 B)
B) 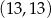 C)
C) 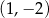 D)
D) 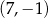
W układzie współrzędnych zaznaczono dwa punkty: 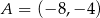 i
i 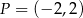 . Punkt
. Punkt 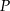 jest środkiem odcinka
jest środkiem odcinka 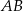 . Jakie współrzędne ma punkt
. Jakie współrzędne ma punkt 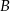 ?
?
A) 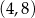 B)
B) 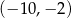 C)
C) 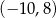 D)
D) 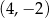
Punkt 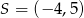 jest środkiem odcinka
jest środkiem odcinka 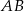 i
i 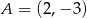 . Punkt
. Punkt 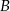 ma współrzędne
ma współrzędne
A) 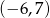 B)
B) 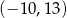 C)
C) 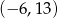 D)
D) 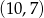
Punkt 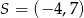 jest środkiem odcinka
jest środkiem odcinka 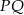 , gdzie
, gdzie 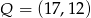 . Zatem punkt
. Zatem punkt 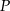 ma współrzędne
ma współrzędne
A) 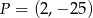 B)
B) 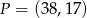 C)
C) 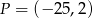 D)
D) 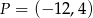
Na czworokącie 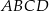 opisano okrąg o środku
opisano okrąg o środku 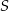 i promieniu
i promieniu 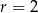 (zobacz rysunek). Pole tego czworokąta jest równe
(zobacz rysunek). Pole tego czworokąta jest równe
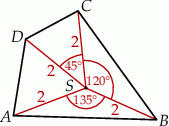
A) 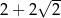 B) 4 C)
B) 4 C) 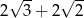 D)
D) 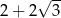
Na prostej o równaniu 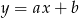 leżą punkty
leżą punkty 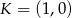 i
i 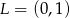 . Wynika stąd, że
. Wynika stąd, że
A) 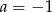 i
i 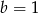 B)
B) 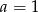 i
i 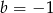 C)
C) 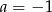 i
i 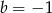 D)
D) 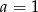 i
i 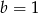
Na prostej o równaniu 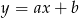 leżą punkty
leżą punkty 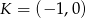 i
i 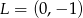 . Wynika stąd, że
. Wynika stąd, że
A) 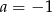 i
i 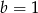 B)
B) 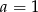 i
i 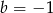 C)
C) 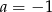 i
i 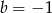 D)
D) 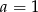 i
i 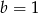
Przekrój osiowy stożka jest trójkątem równobocznym o boku  . Objętość tego stożka wyraża się wzorem
. Objętość tego stożka wyraża się wzorem
A) 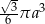 B)
B) 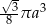 C)
C) 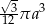 D)
D) 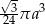
Przekrój osiowy stożka jest równoramiennym trójkątem prostokątnym o przyprostokątnej długości  . Objętość tego stożka wyraża się wzorem
. Objętość tego stożka wyraża się wzorem
A) 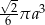 B)
B) 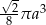 C)
C) 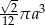 D)
D) 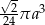
W ostrosłupie prawidłowym trójkątnym krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 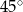 , a wysokość ostrosłupa jest równa 6. Wysokość podstawy tego ostrosłupa ma długość
, a wysokość ostrosłupa jest równa 6. Wysokość podstawy tego ostrosłupa ma długość
A) 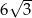 B) 9 C) 12 D)
B) 9 C) 12 D) 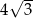
Dany jest trójkąt 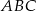 , w którym
, w którym 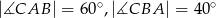 . Odcinki
. Odcinki 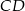 i
i 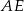 są dwusiecznymi kątów przy wierzchołkach
są dwusiecznymi kątów przy wierzchołkach 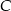 i
i 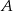 tego trójkąta. Zatem kąt
tego trójkąta. Zatem kąt  zaznaczony na rysunku ma miarę:
zaznaczony na rysunku ma miarę:
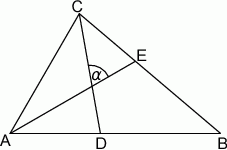
A) 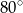 B)
B) 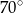 C)
C) 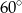 D)
D) 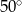
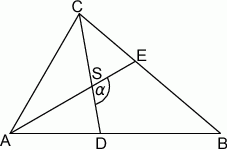
Dany jest trójkąt 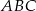 , w którym
, w którym 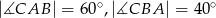 . Odcinki
. Odcinki 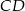 i
i 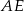 są dwusiecznymi kątów przy wierzchołkach
są dwusiecznymi kątów przy wierzchołkach 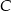 i
i 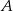 tego trójkąta. Zatem kąt
tego trójkąta. Zatem kąt  zaznaczony na rysunku ma miarę:
zaznaczony na rysunku ma miarę:
A) 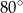 B)
B) 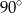 C)
C) 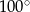 D)
D) 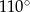
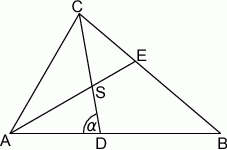
Dany jest trójkąt 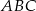 , w którym
, w którym 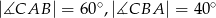 . Odcinki
. Odcinki 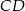 i
i 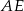 są dwusiecznymi kątów przy wierzchołkach
są dwusiecznymi kątów przy wierzchołkach 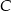 i
i 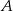 tego trójkąta. Zatem kąt
tego trójkąta. Zatem kąt  zaznaczony na rysunku ma miarę:
zaznaczony na rysunku ma miarę:
A) 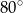 B)
B) 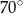 C)
C) 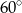 D)
D) 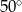
Liczba punktów wspólnych okręgu o równaniu 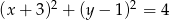 z osiami układu współrzędnych jest równa
z osiami układu współrzędnych jest równa
A) 0 B) 1 C) 2 D) 4
Liczba punktów wspólnych okręgu o równaniu 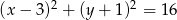 z osiami układu współrzędnych jest równa
z osiami układu współrzędnych jest równa
A) 0 B) 1 C) 2 D) 4
Liczba punktów wspólnych okręgu o równaniu 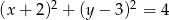 z osiami układu współrzędnych jest równa
z osiami układu współrzędnych jest równa
A) 0 B) 1 C) 2 D) 4
Odcinki 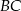 i
i 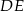 są równoległe. Długości odcinków
są równoległe. Długości odcinków 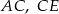 i
i 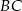 są podane na rysunku.
są podane na rysunku.
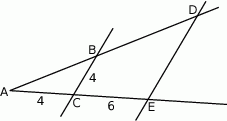
Długość odcinka 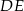 jest równa
jest równa
A) 6 B) 8 C) 10 D) 12
Odcinki 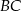 i
i 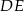 są równoległe. Długości odcinków
są równoległe. Długości odcinków 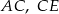 i
i 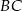 są podane na rysunku.
są podane na rysunku.
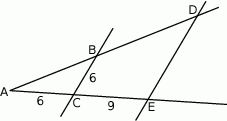
Długość odcinka 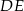 jest równa
jest równa
A) 18 B) 15 C) 12 D) 9
Proste o równaniach 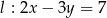 i
i 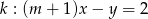 są równoległe. Wynika stąd, że
są równoległe. Wynika stąd, że
A) 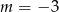 B)
B) 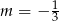 C)
C) 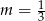 D)
D) 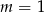
Dana jest prosta 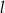 o równaniu
o równaniu 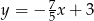 . Prosta
. Prosta 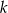 o równaniu
o równaniu 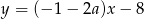 jest równoległa do prostej
jest równoległa do prostej 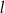 . Wynika stąd, że
. Wynika stąd, że  wynosi
wynosi
A) 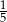 B)
B) 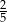 C) 2 D)
C) 2 D) 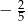
Proste o równaniach 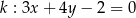 i
i 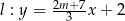 są równoległe, gdy
są równoległe, gdy
A) 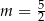 B)
B) 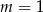 C)
C) 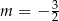 D)
D) 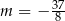
Proste o równaniach 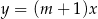 oraz
oraz 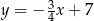 są równoległe. Wtedy
są równoległe. Wtedy
A) 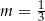 B)
B) 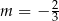 C)
C) 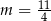 D)
D) 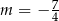
Proste o równaniach 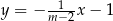 i
i 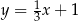 są równoległe. Wynika stąd, że
są równoległe. Wynika stąd, że
A) 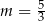 B)
B) 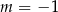 C)
C) 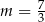 D)
D) 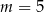
Dane są proste 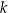 i
i 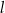 o równaniach
o równaniach
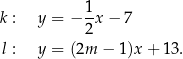
Proste 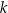 oraz
oraz 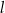 są równoległe, gdy
są równoległe, gdy
A) 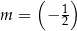 B)
B) 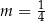 C)
C) 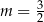 D)
D) 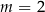
Proste o równaniach 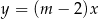 oraz
oraz 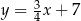 są równoległe. Wtedy
są równoległe. Wtedy
A) 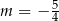 B)
B) 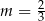 C)
C) 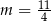 D)
D) 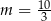
Proste o równaniach 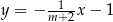 i
i 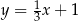 są równoległe. Wynika stąd, że
są równoległe. Wynika stąd, że
A) 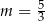 B)
B) 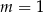 C)
C) 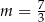 D)
D) 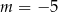
Proste o równaniach 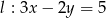 i
i 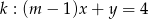 są równoległe. Wynika stąd, że
są równoległe. Wynika stąd, że
A) 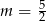 B)
B) 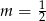 C)
C) 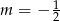 D)
D) 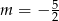
Dane są proste 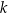 i
i 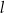 o równaniach
o równaniach
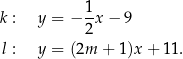
Proste 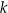 oraz
oraz 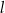 są równoległe, gdy
są równoległe, gdy
A) 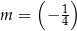 B)
B) 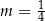 C)
C) 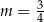 D)
D) 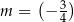
Proste o równaniach 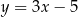 oraz
oraz 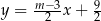 są równoległe, gdy
są równoległe, gdy
A) 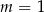 B)
B) 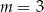 C)
C) 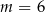 D)
D) 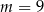
Proste o równaniach 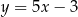 oraz
oraz 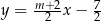 są równoległe, gdy
są równoległe, gdy
A) 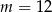 B)
B) 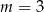 C)
C) 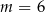 D)
D) 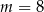
Długość okręgu wpisanego w trójkąt równoboczny wynosi 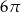 . Długość boku tego trójkąta jest równa
. Długość boku tego trójkąta jest równa
A) 9 B) 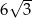 C)
C) 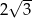 D) 6
D) 6
W trójkącie prostokątnym kąty ostre oznaczono  i
i 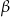 ,
, 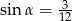 . Jaką miarę ma
. Jaką miarę ma 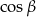 ?
?
A) 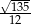 B)
B) 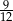 C)
C) 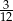 D)
D) 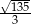
Podstawą graniastosłupa prostego jest prostokąt o bokach długości 7 i 3. Kąt  , jaki przekątna tego graniastosłupa tworzy z jedną z krawędzi górnej podstawy jest równy
, jaki przekątna tego graniastosłupa tworzy z jedną z krawędzi górnej podstawy jest równy 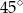 (zobacz rysunek).
(zobacz rysunek).
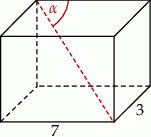
Wysokość graniastosłupa jest równa
A) 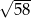 B)
B) 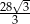 C)
C) 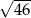 D)
D) 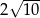
Przekrój osiowy stożka jest trójkątem prostokątnym o przeciwprostokątnej długości 6. Objętość tego stożka jest równa
A) 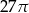 B)
B) 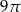 C)
C) 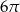 D)
D) 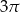
Przekrój osiowy stożka jest trójkątem prostokątnym o przeciwprostokątnej długości 8. Objętość tego stożka jest równa
A) 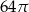 B)
B) 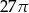 C)
C) 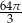 D)
D) 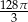
Różnica liczby krawędzi i liczby wierzchołków ostrosłupa jest równa 11. Podstawą tego ostrosłupa jest
A) dziesięciokąt. B) jedenastokąt. C) dwunastokąt. D) trzynastokąt.
W pewnym ostrosłupie prawidłowym stosunek liczby 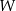 wszystkich wierzchołków do liczby
wszystkich wierzchołków do liczby 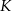 wszystkich krawędzi jest równy
wszystkich krawędzi jest równy 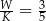 . Podstawą tego ostrosłupa jest
. Podstawą tego ostrosłupa jest
A) kwadrat. B) pięciokąt foremny.
C) sześciokąt foremny. D) siedmiokąt foremny.
W pewnym ostrosłupie prawidłowym stosunek liczby 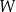 wszystkich wierzchołków do liczby
wszystkich wierzchołków do liczby 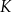 wszystkich krawędzi jest równy
wszystkich krawędzi jest równy 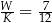 . Podstawą tego ostrosłupa jest
. Podstawą tego ostrosłupa jest
A) kwadrat. B) pięciokąt foremny.
C) sześciokąt foremny. D) siedmiokąt foremny.
Różnica liczby krawędzi i liczby wierzchołków ostrosłupa jest równa 10. Podstawą tego ostrosłupa jest
A) dziesięciokąt. B) jedenastokąt. C) dwunastokąt. D) trzynastokąt.
Na trójkącie równobocznym opisano koło, którego pole jest równe 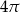 . Długość boku tego trójkąta jest równa
. Długość boku tego trójkąta jest równa
A) 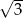 B)
B) 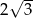 C)
C) 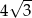 D) 3
D) 3
Pole koła wpisanego w trójkąt równoboczny jest równe 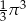 . Długość boku tego trójkąta jest równa
. Długość boku tego trójkąta jest równa
A) 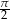 B)
B) 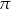 C)
C) 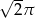 D)
D) 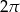
Na trójkącie równobocznym opisano koło, którego pole jest równe 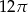 . Długość boku tego trójkąta jest równa
. Długość boku tego trójkąta jest równa
A) 6 B) 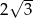 C)
C) 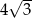 D) 3
D) 3
Na trójkącie równobocznym opisano koło, którego pole jest równe 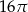 . Długość boku tego trójkąta jest równa
. Długość boku tego trójkąta jest równa
A) 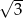 B)
B) 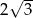 C)
C) 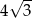 D) 3
D) 3
Pole koła opisanego na trójkącie równobocznym jest równe 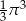 . Długość boku tego trójkąta jest równa
. Długość boku tego trójkąta jest równa
A) 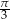 B)
B) 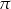 C)
C) 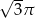 D)
D)