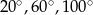W trójkącie prostokątnym przeciwprostokątna ma długość 4. Pole koła opisanego na tym trójkącie wynosi
A) 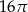 B)
B) 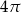 C)
C) 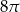 D)
D) 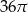
/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Trójkąt
Pole koła opisanego na trójkącie prostokątnym o bokach długości 10, 24, 26 jest równe
A) 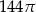 B)
B) 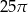 C)
C) 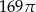 D)
D) 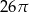
Na rysunku przedstawiono okrąg wpisany w trójkąt.
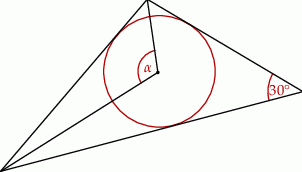
Miara kąta  jest równa
jest równa
A) 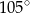 B)
B) 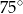 C)
C) 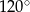 D)
D) 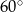
Okrąg o środku w punkcie 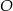 jest wpisany w trójkąt
jest wpisany w trójkąt 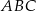 . Wiadomo, że
. Wiadomo, że 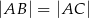 i
i 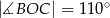 (zobacz rysunek).
(zobacz rysunek).
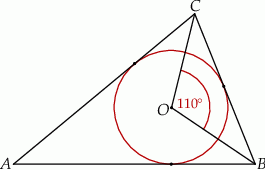
Miara kąta 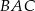 jest równa
jest równa
A) 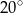 B)
B) 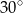 C)
C) 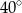 D)
D) 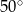
Okrąg o środku w punkcie 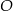 jest wpisany w trójkąt
jest wpisany w trójkąt 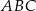 . Wiadomo, że
. Wiadomo, że 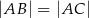 i
i 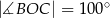 (zobacz rysunek).
(zobacz rysunek).
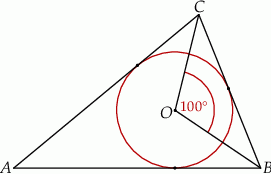
Miara kąta 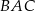 jest równa
jest równa
A) 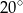 B)
B) 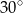 C)
C) 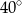 D)
D) 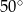
W trójkącie prostokątnym miary kątów ostrych są równe  i
i 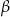 . Wartość wyrażenia
. Wartość wyrażenia 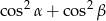 jest równa
jest równa
A) 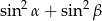 B)
B) 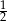 C)
C) 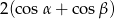 D)
D) 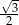
Każde z ramion trójkąta równoramiennego ma długość 20. Kąt zawarty między ramionami tego trójkąta ma miarę 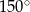 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 100 B) 200 C) 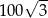 D)
D) 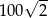
Każde z ramion trójkąta równoramiennego ma długość 20. Kąt zawarty między ramionami tego trójkąta ma miarę 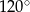 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 100 B) 200 C) 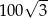 D)
D) 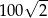
Pole powierzchni trójkąta równoramiennego o ramionach długości 6 cm i kącie między nimi 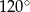 jest równe
jest równe
A) 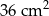 B)
B) 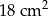 C)
C) 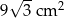 D)
D) 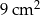
Ramię trójkąta równoramiennego 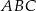 ma długość 8, a jeden z kątów tego trójkąta ma miarę
ma długość 8, a jeden z kątów tego trójkąta ma miarę 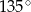 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 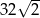 B)
B) 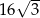 C) 32 D)
C) 32 D) 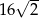
Suma kwadratów długości wszystkich boków trójkąta prostokątnego jest równa 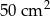 . Zatem promień okręgu opisanego na tym trójkącie ma długość:
. Zatem promień okręgu opisanego na tym trójkącie ma długość:
A) 10 cm B) 7,5 cm C) 5 cm D) 2,5 cm
Suma kwadratów długości wszystkich boków trójkąta prostokątnego jest równa 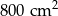 . Zatem promień okręgu opisanego na tym trójkącie ma długość:
. Zatem promień okręgu opisanego na tym trójkącie ma długość:
A) 10 cm B) 7,5 cm C) 5 cm D) 2,5 cm
Suma kwadratów długości wszystkich boków trójkąta prostokątnego jest równa 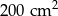 . Zatem promień okręgu opisanego na tym trójkącie ma długość:
. Zatem promień okręgu opisanego na tym trójkącie ma długość:
A) 10 cm B) 7,5 cm C) 5 cm D) 2,5 cm
W trójkącie 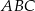 , w którym
, w którym 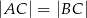 , na boku
, na boku 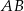 wybrano punkt
wybrano punkt  taki, że
taki, że 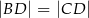 oraz
oraz 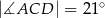 (zobacz rysunek).
(zobacz rysunek).
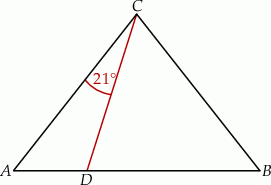
Wynika stąd, że kąt  ma miarę
ma miarę
A) 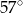 B)
B) 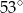 C)
C) 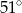 D)
D) 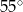
Dany jest trójkąt równoramienny 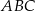 , w którym
, w którym 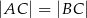 . Na podstawie
. Na podstawie 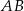 tego trójkąta leży punkt
tego trójkąta leży punkt  , taki że
, taki że 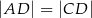 ,
, 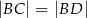 oraz
oraz 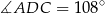 (zobacz rysunek).
(zobacz rysunek).
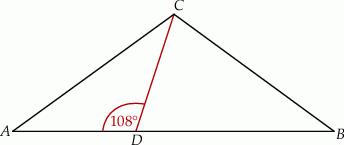
Wynika stąd, że kąt 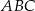 ma miarę
ma miarę
A) 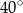 B)
B) 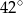 C)
C) 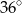 D)
D) 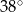
Dany jest trójkąt równoramienny 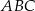 , w którym
, w którym 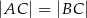 . Na podstawie
. Na podstawie 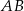 tego trójkąta leży punkt
tego trójkąta leży punkt 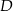 , taki że
, taki że 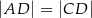 ,
, 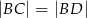 oraz
oraz 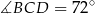 (zobacz rysunek).
(zobacz rysunek).
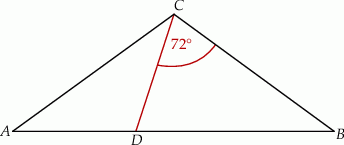
Wynika stąd, że kąt 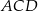 ma miarę
ma miarę
A) 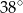 B)
B) 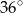 C)
C) 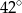 D)
D) 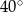
W trójkącie 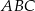 , w którym
, w którym 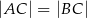 , na boku
, na boku 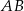 wybrano punkt
wybrano punkt 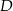 taki, że
taki, że 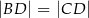 oraz
oraz 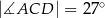 (zobacz rysunek).
(zobacz rysunek).
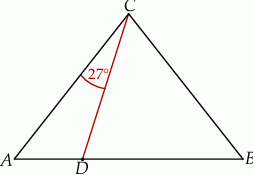
Wynika stąd, że kąt 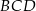 ma miarę
ma miarę
A) 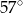 B)
B) 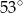 C)
C) 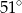 D)
D) 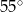
W trójkącie jeden z kątów jest o 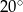 większy od najmniejszego, a trzeci kąt jest trzykrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
większy od najmniejszego, a trzeci kąt jest trzykrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
A) 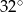 B)
B) 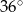 C)
C) 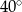 D)
D) 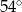
W trójkącie jeden z kątów jest o 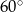 większy od najmniejszego, a trzeci kąt jest czterokrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
większy od najmniejszego, a trzeci kąt jest czterokrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
A) 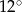 B)
B) 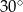 C)
C) 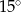 D)
D) 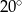
W trójkącie miary kątów są równe:  ,
, 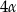 ,
, 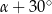 . Miara największego kąta tego trójkąta jest równa
. Miara największego kąta tego trójkąta jest równa
A) 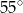 B)
B) 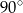 C)
C) 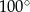 D)
D) 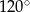
W trójkącie jeden z kątów jest o 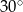 większy od najmniejszego, a trzeci kąt jest trzykrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
większy od najmniejszego, a trzeci kąt jest trzykrotnie większy od najmniejszego. Najmniejszy z kątów tego trójkąta ma miarę
A) 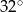 B)
B) 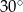 C)
C) 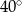 D)
D) 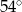
Jeden z kątów trójkąta jest trzy razy większy od drugiego. Miara trzeciego kąta jest o 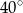 większa od miary najmniejszego kąta w tym trójkącie. Miary kątów tego trójkąta są równe
większa od miary najmniejszego kąta w tym trójkącie. Miary kątów tego trójkąta są równe
A) 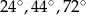 B)
B) 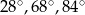 C)
C) 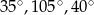 D)
D)