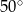Dany jest trójkąt prostokątny (patrz rysunek).
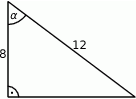
Wartość wyrażenia 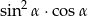 wynosi
wynosi
A) 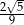 B)
B)  C)
C) 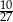 D)
D) 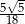
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dany jest trójkąt prostokątny (patrz rysunek).

Wartość wyrażenia 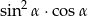 wynosi
wynosi
A) 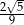 B)
B)  C)
C) 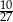 D)
D) 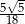
Dany jest trójkąt o bokach długości 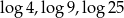 . Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
. Trójkątem podobnym do tego trójkąta jest trójkąt, którego boki mają długości
A) 2, 3, 5 B) 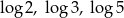 C)
C) 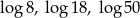 D) 4, 9, 25
D) 4, 9, 25
Odcinek 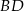 jest zawarty w dwusiecznej kąta ostrego
jest zawarty w dwusiecznej kąta ostrego 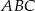 trójkąta prostokątnego, w którym przyprostokątne
trójkąta prostokątnego, w którym przyprostokątne 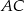 i
i 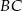 mają długości odpowiednio 5 i 3.
mają długości odpowiednio 5 i 3.
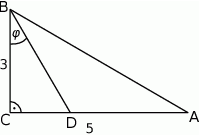
Wówczas miara 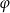 kąta
kąta 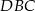 spełnia warunek
spełnia warunek
A) 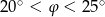 B)
B) 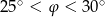 C)
C) 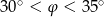 D)
D) 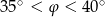
Odcinek 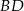 jest zawarty w dwusiecznej kąta ostrego
jest zawarty w dwusiecznej kąta ostrego 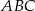 trójkąta prostokątnego, w którym przyprostokątne
trójkąta prostokątnego, w którym przyprostokątne 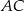 i
i 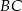 mają długości odpowiednio 8 i 3.
mają długości odpowiednio 8 i 3.
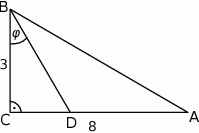
Wówczas miara 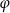 kąta
kąta 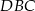 spełnia warunek
spełnia warunek
A) 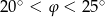 B)
B) 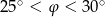 C)
C) 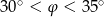 D)
D) 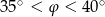
Pole trójkąta prostokątnego jest równe 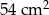 . Różnica długości przyprostokątnych wynosi 3 cm. Jaką długość ma przeciwprostokątna tego trójkąta?
. Różnica długości przyprostokątnych wynosi 3 cm. Jaką długość ma przeciwprostokątna tego trójkąta?
A) 14 B) 15 C) 16 D) 17
Symetralne boków trójkąta prostokątnego przecinają się w punkcie odległym od wierzchołka kąta prostego o 5 cm. Przeciwprostokątna tego trójkąta ma długość
A) 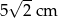 B)
B) 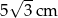 C)
C) 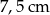 D)
D) 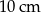
Symetralne boków trójkąta prostokątnego przecinają się w punkcie odległym od wierzchołka kąta prostego o 3 cm. Przeciwprostokątna tego trójkąta ma długość
A) 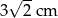 B)
B) 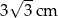 C)
C) 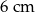 D)
D) 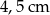
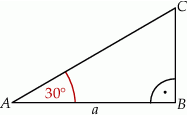
Obwód trójkąta 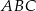 , przedstawionego na rysunku, jest równy
, przedstawionego na rysunku, jest równy
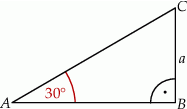
A) 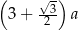 B)
B) 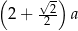 C)
C) 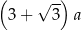 D)
D) 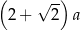
Obwód trójkąta 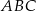 , przedstawionego na rysunku, jest równy
, przedstawionego na rysunku, jest równy
A) 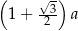 B)
B) 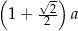 C)
C) 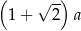 D)
D) 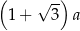
Pole trójkąta 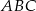 jest równe 17, a jego obwód 22. Jaki jest obwód trójkąta o polu 68, podobnego do trójkąta
jest równe 17, a jego obwód 22. Jaki jest obwód trójkąta o polu 68, podobnego do trójkąta 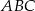 ?
?
A) 34 B) 44 C) 51 D) 88
Trójkąty 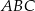 oraz
oraz 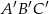 są podobne. Obwód trójkąta
są podobne. Obwód trójkąta 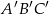 jest równy 12, a jego pole 6. Jeżeli pole trójkąta
jest równy 12, a jego pole 6. Jeżeli pole trójkąta 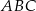 jest równe
jest równe 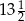 , to jego obwód wynosi
, to jego obwód wynosi
A) 18 B) 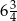 C) 27 D) 9
C) 27 D) 9
Dany jest trójkąt prostokątny o kącie prostym przy wierzchołku 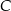 . Środkowa
. Środkowa 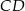 tworzy z przyprostokątną
tworzy z przyprostokątną 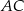 kąt
kąt 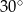 . Wynika stąd, że kąt między tą środkową a wysokością
. Wynika stąd, że kąt między tą środkową a wysokością 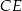 trójkąta ma miarę
trójkąta ma miarę
A) 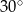 B)
B) 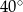 C)
C) 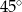 D)
D) 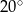
Dany jest trójkąt prostokątny o kącie prostym przy wierzchołku 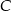 . Środkowa
. Środkowa 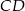 tworzy z przyprostokątną
tworzy z przyprostokątną 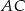 kąt
kąt 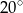 . Wynika stąd, że kąt między tą środkową a wysokością
. Wynika stąd, że kąt między tą środkową a wysokością 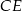 trójkąta ma miarę
trójkąta ma miarę
A) 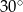 B)
B) 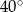 C)
C) 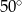 D)
D) 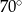
Dany jest trójkąt prostokątny o kącie prostym przy wierzchołku 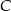 . Środkowa
. Środkowa 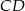 tworzy z przyprostokątną
tworzy z przyprostokątną 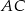 kąt
kąt 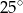 . Wynika stąd, że kąt między tą środkową a wysokością
. Wynika stąd, że kąt między tą środkową a wysokością 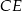 trójkąta ma miarę
trójkąta ma miarę
A) 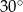 B)
B) 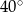 C)
C) 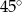 D)
D) 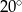
Dany jest trójkąt 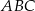 , w którym
, w którym 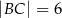 . Miara kąta
. Miara kąta 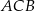 jest równa
jest równa 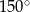 (zobacz rysunek).
(zobacz rysunek).
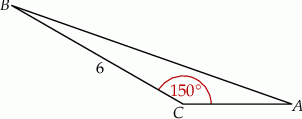
Wysokość trójkąta 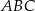 opuszczona z wierzchołka
opuszczona z wierzchołka 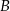 jest równa
jest równa
A) 3 B) 4 C) 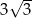 D)
D) 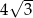
Jeden kąt trójkąta ma miarę 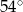 . Z pozostałych dwóch kątów tego trójkąta jeden jest 6 razy większy od drugiego. Miary pozostałych kątów są równe
. Z pozostałych dwóch kątów tego trójkąta jeden jest 6 razy większy od drugiego. Miary pozostałych kątów są równe
A) 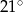 i
i 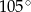 B)
B) 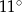 i
i 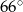 C)
C) 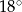 i
i 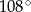 D)
D) 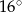 i
i 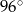
Jeden kąt trójkąta ma miarę 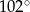 . Z pozostałych dwóch kątów tego trójkąta jeden jest 5 razy większy od drugiego. Miary pozostałych kątów są równe
. Z pozostałych dwóch kątów tego trójkąta jeden jest 5 razy większy od drugiego. Miary pozostałych kątów są równe
A) 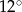 i
i 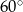 B)
B) 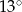 i
i 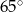 C)
C) 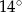 i
i 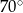 D)
D) 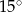 i
i 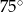
Jeden z kątów wewnętrznych trójkąta ma 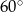 , a miary dwóch pozostałych kątów pozostają w stosunku jak 1:4. Miara kąta rozwartego tego trójkąta wynosi
, a miary dwóch pozostałych kątów pozostają w stosunku jak 1:4. Miara kąta rozwartego tego trójkąta wynosi
A) 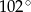 B)
B) 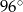 C)
C) 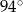 D)
D) 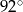
Przyprostokątna 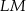 trójkąta prostokątnego
trójkąta prostokątnego 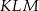 ma długość 3, a przeciwprostokątna
ma długość 3, a przeciwprostokątna 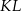 ma długość 8 (zobacz rysunek).
ma długość 8 (zobacz rysunek).
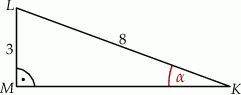
Wtedy miara  kąta ostrego
kąta ostrego 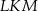 tego trójkąta spełnia warunek
tego trójkąta spełnia warunek
A) 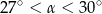 B)
B) 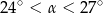 C)
C) 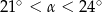 D)
D) 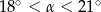
Przyprostokątna 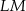 trójkąta prostokątnego
trójkąta prostokątnego 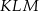 ma długość 3, a przeciwprostokątna
ma długość 3, a przeciwprostokątna 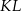 ma długość 8 (zobacz rysunek).
ma długość 8 (zobacz rysunek).
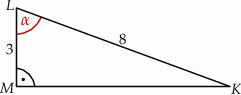
Wtedy miara  kąta ostrego
kąta ostrego 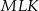 tego trójkąta spełnia warunek
tego trójkąta spełnia warunek
A) 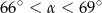 B)
B) 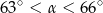 C)
C) 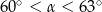 D)
D) 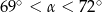
Kwadrat i trójkąt równoboczny mają równe pola. Stosunek długości boku kwadratu do długości boku trójkąta równobocznego jest wtedy równy
A) 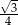 B)
B) 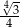 C)
C) 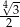 D)
D) 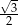
Kwadrat i trójkąt równoboczny mają równe pola. Stosunek długości boku trójkąta równobocznego do długości boku kwadratu jest wtedy równy
A) 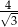 B)
B) 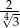 C)
C) 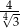 D)
D) 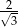
Trójkąt 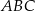 jest prostokątny. Odcinek
jest prostokątny. Odcinek 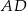 jest wysokością tego trójkąta poprowadzoną z wierzchołka
jest wysokością tego trójkąta poprowadzoną z wierzchołka 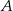 na przeciwprostokątną
na przeciwprostokątną 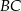 . Wtedy
. Wtedy
A) 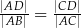 B)
B) 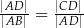 C)
C) 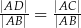 D)
D) 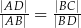
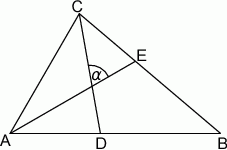
Dany jest trójkąt 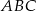 , w którym
, w którym 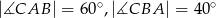 . Odcinki
. Odcinki 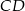 i
i 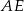 są dwusiecznymi kątów przy wierzchołkach
są dwusiecznymi kątów przy wierzchołkach 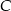 i
i 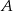 tego trójkąta. Zatem kąt
tego trójkąta. Zatem kąt  zaznaczony na rysunku ma miarę:
zaznaczony na rysunku ma miarę:
A) 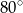 B)
B) 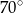 C)
C) 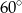 D)
D) 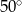
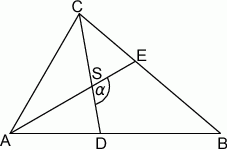
Dany jest trójkąt 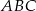 , w którym
, w którym 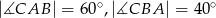 . Odcinki
. Odcinki 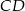 i
i 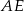 są dwusiecznymi kątów przy wierzchołkach
są dwusiecznymi kątów przy wierzchołkach 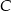 i
i 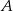 tego trójkąta. Zatem kąt
tego trójkąta. Zatem kąt  zaznaczony na rysunku ma miarę:
zaznaczony na rysunku ma miarę:
A) 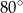 B)
B) 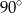 C)
C) 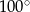 D)
D) 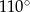
Dany jest trójkąt 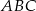 , w którym
, w którym 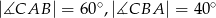 . Odcinki
. Odcinki 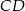 i
i 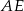 są dwusiecznymi kątów przy wierzchołkach
są dwusiecznymi kątów przy wierzchołkach 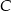 i
i 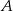 tego trójkąta. Zatem kąt
tego trójkąta. Zatem kąt  zaznaczony na rysunku ma miarę:
zaznaczony na rysunku ma miarę:
A) 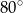 B)
B) 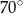 C)
C) 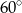 D)
D) 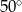
Długość okręgu wpisanego w trójkąt równoboczny wynosi 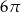 . Długość boku tego trójkąta jest równa
. Długość boku tego trójkąta jest równa
A) 9 B) 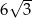 C)
C) 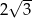 D) 6
D) 6
W trójkącie prostokątnym kąty ostre oznaczono  i
i 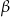 ,
, 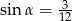 . Jaką miarę ma
. Jaką miarę ma 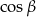 ?
?
A) 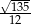 B)
B) 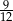 C)
C) 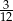 D)
D) 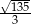
Na trójkącie równobocznym opisano koło, którego pole jest równe 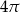 . Długość boku tego trójkąta jest równa
. Długość boku tego trójkąta jest równa
A) 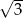 B)
B) 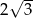 C)
C) 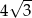 D) 3
D) 3
Pole koła wpisanego w trójkąt równoboczny jest równe 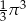 . Długość boku tego trójkąta jest równa
. Długość boku tego trójkąta jest równa
A) 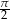 B)
B) 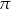 C)
C) 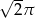 D)
D) 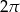
Na trójkącie równobocznym opisano koło, którego pole jest równe 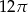 . Długość boku tego trójkąta jest równa
. Długość boku tego trójkąta jest równa
A) 6 B) 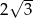 C)
C) 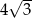 D) 3
D) 3
Na trójkącie równobocznym opisano koło, którego pole jest równe 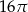 . Długość boku tego trójkąta jest równa
. Długość boku tego trójkąta jest równa
A) 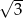 B)
B) 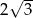 C)
C) 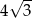 D) 3
D) 3
Pole koła opisanego na trójkącie równobocznym jest równe 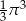 . Długość boku tego trójkąta jest równa
. Długość boku tego trójkąta jest równa
A) 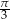 B)
B) 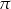 C)
C) 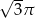 D)
D) 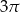
W trójkącie prostokątnym o przyprostokątnych długości 4 i 5 połączono wierzchołek 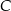 kąta prostego ze środkiem
kąta prostego ze środkiem 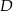 przeciwprostokątnej. Długość odcinka
przeciwprostokątnej. Długość odcinka 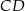 jest równa
jest równa
A) 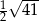 B) 4,5 C) 4 D)
B) 4,5 C) 4 D) 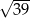
W trójkącie prostokątnym o przyprostokątnych długości 5 i 12 połączono wierzchołek 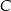 kąta prostego ze środkiem
kąta prostego ze środkiem 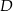 przeciwprostokątnej. Długość odcinka
przeciwprostokątnej. Długość odcinka 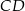 jest równa
jest równa
A) 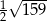 B) 6,5 C) 13 D)
B) 6,5 C) 13 D) 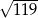
W trójkącie prostokątnym o przyprostokątnych długości 6 i 8 połączono wierzchołek 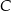 kąta prostego ze środkiem
kąta prostego ze środkiem 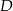 przeciwprostokątnej. Długość odcinka
przeciwprostokątnej. Długość odcinka 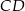 jest równa
jest równa
A) 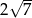 B) 10 C) 7 D) 5
B) 10 C) 7 D) 5
W trójkącie prostokątnym o przyprostokątnych długości 7 i 24 połączono wierzchołek 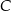 kąta prostego ze środkiem
kąta prostego ze środkiem 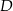 przeciwprostokątnej. Długość odcinka
przeciwprostokątnej. Długość odcinka 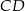 jest równa
jest równa
A) 25 B) 12 C) 15 D) 12,5
Długości boków trójkąta prostokątnego wynoszą 8 cm, 15 cm, 17 cm. Odcinek łączący środek przeciwprostokątnej z wierzchołkiem kąta prostego tego trójkąta ma długość
A) 8 cm B) 7,5 cm C) 9 cm D) 8,5 cm
Pole trójkąta prostokątnego 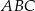 , przedstawionego na rysunku, jest równe
, przedstawionego na rysunku, jest równe
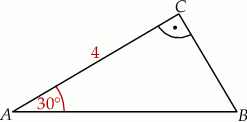
A) 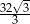 B)
B) 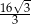 C)
C) 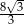 D)
D) 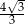
Pole trójkąta prostokątnego 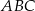 , przedstawionego na rysunku, jest równe
, przedstawionego na rysunku, jest równe
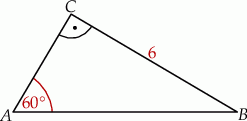
A) 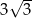 B)
B) 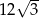 C)
C) 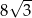 D)
D) 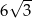
Punkty 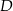 ,
, 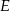 i
i 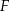 są punktami styczności okręgu wpisanego w trójkąt
są punktami styczności okręgu wpisanego w trójkąt 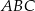 z jego bokami i
z jego bokami i 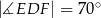 (zobacz rysunek).
(zobacz rysunek).
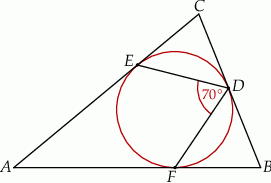
Miara kąta 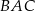 jest równa
jest równa
A) 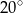 B)
B) 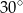 C)
C) 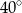 D)
D)