Naprzeciwko boków 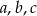 trójkąta
trójkąta 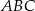 znajdują się odpowiednio kąty
znajdują się odpowiednio kąty 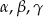 . Wiadomo, że
. Wiadomo, że 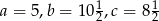 . Wówczas
. Wówczas
A) 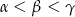 B)
B) 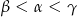 C)
C) 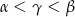 D)
D) 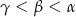
/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Trójkąt
Naprzeciwko boków 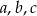 trójkąta
trójkąta 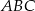 znajdują się odpowiednio kąty
znajdują się odpowiednio kąty 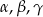 . Wiadomo, że
. Wiadomo, że 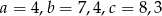 . Wówczas
. Wówczas
A) 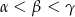 B)
B) 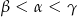 C)
C) 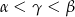 D)
D) 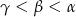
Naprzeciwko boków 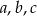 trójkąta
trójkąta 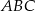 znajdują się odpowiednio kąty
znajdują się odpowiednio kąty 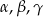 . Wiadomo, że
. Wiadomo, że 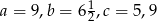 . Wówczas
. Wówczas
A) 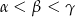 B)
B) 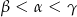 C)
C) 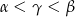 D)
D) 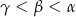
Miary kątów trójkąta pozostają w stosunku 4:5:6. Miary kątów tego trójkąta są równe
A) 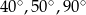 B)
B) 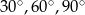 C)
C) 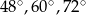 D)
D) 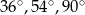
W trójkącie prostokątnym długości przyprostokątnych wynoszą 6 i 8. Stosunek długości odcinków, na które wysokość podzieliła przeciwprostokątną wynosi
A)  B)
B)  C)
C) 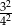 D)
D) 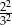
Dany jest trójkąt prostokątny o przyprostokątnych 5 i 12. Poprowadzono wysokość na przeciwprostokątną. Wysokość ta podzieliła przeciwprostokątną na odcinki w stosunku
A) 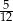 B)
B) 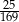 C)
C) 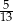 D)
D) 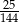
Trójkąt można zbudować z odcinków o długościach:
A) 10, 6, 5 B) 4, 2, 1 C) 8, 5, 3 D) 6, 6, 13
Trójkąt można zbudować z odcinków o długościach:
A) 4, 2, 2 B) 7, 4, 3 C) 5, 6, 12 D) 8, 4, 5
Jeśli 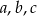 są długościami odcinków, to istnieje trójkąt o bokach
są długościami odcinków, to istnieje trójkąt o bokach 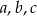 , jeżeli
, jeżeli
A) 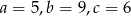
B) 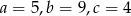
C) 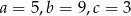
D) 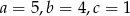
Można zbudować trójkąt z odcinków 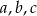 jeśli
jeśli
A) 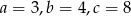
B) 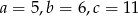
C) 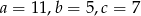
D) 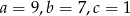
Długościami boków trójkąta mogą być odcinki:
A) 5 cm, 8 cm, 2 cm B) 9 cm, 4 cm, 4 cm C) 3 cm, 2 cm, 1 cm D) 7 cm, 9 cm, 10 cm
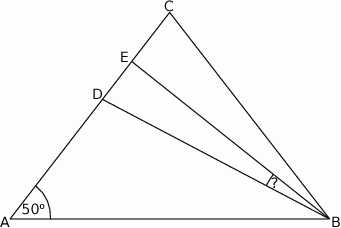
W trójkącie równoramiennym 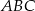 spełnione są warunki:
spełnione są warunki: 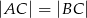 ,
, 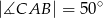 . Odcinek
. Odcinek 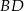 jest dwusieczną kąta
jest dwusieczną kąta 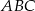 , a odcinek
, a odcinek 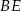 jest wysokością opuszczoną z wierzchołka
jest wysokością opuszczoną z wierzchołka 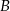 na bok
na bok 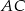 . Miara kąta
. Miara kąta 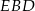 jest równa
jest równa
A) 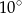 B)
B) 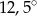 C)
C) 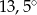 D)
D) 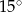
W trójkącie prostokątnym spodek wysokości poprowadzonej na przeciwprostokątną podzielił ją na odcinki długości 6,25 cm oraz 16 cm. Zatem wysokość ta ma długość
A) 15 cm B) 20 cm C) 22,25 cm D) 10 cm
W trójkącie prostokątnym spodek wysokości poprowadzonej na przeciwprostokątną podzielił ją na odcinki długości 3 cm oraz 12 cm. Zatem wysokość ta ma długość
A) 6 cm B) 20 cm C) 22,25 cm D) 10 cm
W trójkącie prostokątnym spodek wysokości poprowadzonej na przeciwprostokątną podzielił ją na odcinki długości 5,5 cm oraz 22 cm. Zatem wysokość ta ma długość
A) 15 cm B) 11 cm C) 22,25 cm D) 10 cm
Na rysunku przedstawiono okrąg o środku 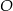 , który jest wpisany w trójkąt
, który jest wpisany w trójkąt  .
.
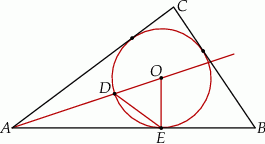
Okrąg ten przecina bok  w punkcie
w punkcie  , a odcinek
, a odcinek 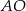 w punkcie
w punkcie 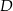 . Jeżeli
. Jeżeli 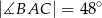 , to miara kąta
, to miara kąta 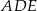 jest równa
jest równa
A) 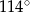 B)
B) 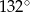 C)
C) 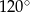 D)
D) 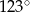
W trójkącie 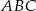 na rysunku obok dane są:
na rysunku obok dane są: 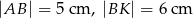 oraz
oraz 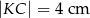 . Wiadomo, że
. Wiadomo, że 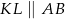 .
.
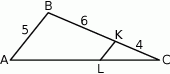
Wówczas:
A) 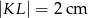 B)
B) 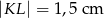 C)
C) 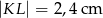 D)
D) 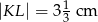
W trójkącie 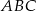 punkt
punkt 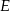 leży na boku
leży na boku 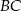 , a punkt
, a punkt 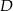 leży na boku
leży na boku 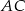 . Odcinek
. Odcinek 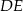 jest równoległy do boku
jest równoległy do boku 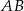 , a ponadto
, a ponadto 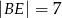 ,
, 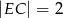 i
i 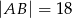 (zobacz rysunek).
(zobacz rysunek).
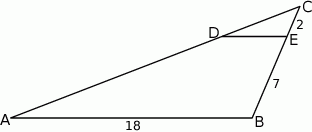
Długość odcinka 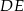 jest równa
jest równa
A) 5 B) 3 C) 6 D) 4
W trójkącie 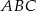 punkt
punkt 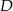 leży na boku
leży na boku 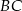 , a punkt
, a punkt 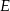 leży na boku
leży na boku 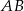 . Odcinek
. Odcinek 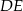 jest równoległy do boku
jest równoległy do boku 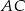 , a ponadto
, a ponadto  ,
, 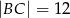 i
i 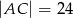 (zobacz rysunek).
(zobacz rysunek).
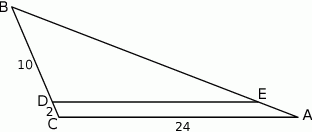
Długość odcinka 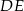 jest równa
jest równa
A) 22 B) 20 C) 12 D) 11
W trójkącie równobocznym długość każdego boku zmniejszono o 20%. Wtedy pole tego trójkąta
A) zmniejszy się o 20% B) zmniejszy się o 40%
C) zmniejszy się o mniej niż 20% D) zmniejszy się o 36%
Kąt  jest najmniejszym z kątów trójkąta prostokątnego o bokach długości
jest najmniejszym z kątów trójkąta prostokątnego o bokach długości 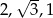 . Wtedy
. Wtedy
A) 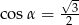 B)
B) 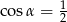 C)
C) 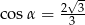 D)
D) 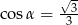
Kąt  jest najmniejszym z kątów trójkąta prostokątnego o bokach długości
jest najmniejszym z kątów trójkąta prostokątnego o bokach długości 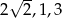 . Wtedy
. Wtedy
A) 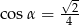 B)
B) 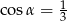 C)
C) 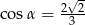 D)
D) 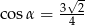
W trójkącie prostokątnym dwa dłuższe boki mają długości 5 i 7. Obwód tego trójkąta jest równy
A) 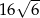 B)
B) 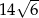 C)
C) 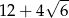 D)
D) 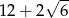
W trójkącie prostokątnym dwa dłuższe boki mają długości 7 i 9. Obwód tego trójkąta jest równy
A) 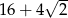 B)
B) 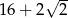 C)
C) 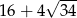 D)
D) 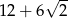
Dwa dłuższe boki trójkąta prostokątnego mają długości 3 cm oraz 4 cm. Długość najkrótszego boku tego trójkąta wynosi
A) 5 cm B) 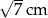 C) 2,6 cm D)
C) 2,6 cm D) 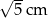
Dany jest trójkąt, którego kąty mają miary 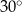 ,
, 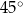 oraz
oraz 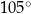 . Długości boków trójkąta, leżących naprzeciwko tych kątów są równe – odpowiednio –
. Długości boków trójkąta, leżących naprzeciwko tych kątów są równe – odpowiednio –  ,
, 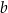 oraz
oraz  (zobacz rysunek).
(zobacz rysunek).

Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A–F. Pole tego trójkąta poprawnie określa wyrażenie
A) 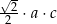 B)
B) 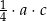 C)
C) 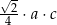
D) 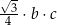 E)
E) 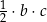 F)
F) 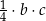
Dany jest trójkąt, którego kąty mają miary 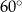 ,
, 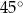 oraz
oraz 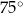 . Długości boków trójkąta, leżących naprzeciwko tych kątów są równe – odpowiednio –
. Długości boków trójkąta, leżących naprzeciwko tych kątów są równe – odpowiednio –  ,
, 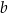 oraz
oraz  (zobacz rysunek).
(zobacz rysunek).
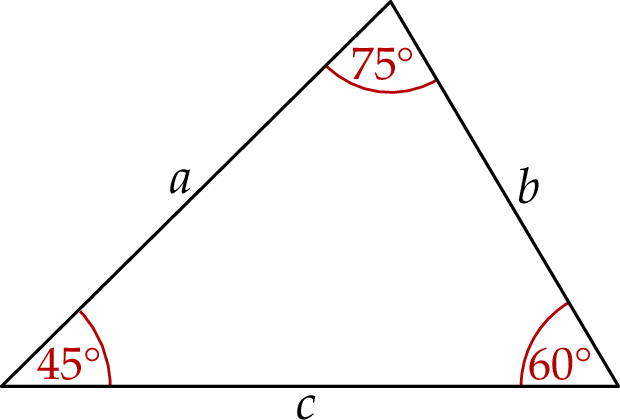
Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A–F. Pole tego trójkąta poprawnie określa wyrażenie
A) 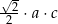 B)
B) 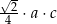 C)
C) 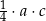
D) 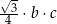 E)
E) 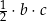 F)
F) 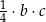
Niech  i
i 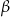 oznaczają miary kątów ostrych w dowolnym trójkącie prostokątnym. Wówczas zachodzi równość:
oznaczają miary kątów ostrych w dowolnym trójkącie prostokątnym. Wówczas zachodzi równość:
A) 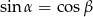 B)
B) 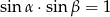 C)
C) 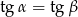 D)
D) 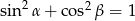
Długości boków trójkąta są liczbami całkowitymi. Jeden bok ma 7 cm, a drugi ma 2 cm. Trzeci bok tego trójkąta może mieć długość
A) 12 cm B) 9 cm C) 6 cm D) 3 cm
Długości boków trójkąta są liczbami całkowitymi. Jeden bok ma 4 cm, a drugi ma 9 cm. Trzeci bok tego trójkąta może mieć długość
A) 4 cm B) 5 cm C) 14 cm D) 9 cm
Jeżeli trójkąty 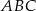 i
i 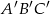 są podobne, a ich obwody są odpowiednio równe 25 cm i 50 cm, to skala podobieństwa trójkątów
są podobne, a ich obwody są odpowiednio równe 25 cm i 50 cm, to skala podobieństwa trójkątów 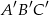 i
i 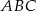 jest równa
jest równa
A) 2 B) 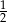 C)
C) 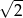 D)
D) 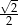
Pole trójkąta równobocznego wpisanego w koło o polu 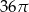 jest równe
jest równe
A) 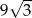 B) 81 C)
B) 81 C) 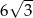 D)
D) 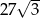
Dane są długości boków 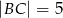 i
i 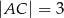 trójkąta prostokątnego
trójkąta prostokątnego 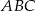 o kącie ostrym
o kącie ostrym 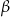 (zobacz rysunek).
(zobacz rysunek).
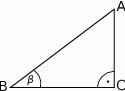
Wtedy
A) 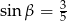 B)
B) 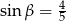 C)
C) 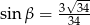 D)
D) 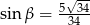
W trójkącie prostokątnym 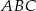 przyprostokątne mają długość
przyprostokątne mają długość 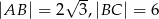 , a kąt
, a kąt  ma miarę
ma miarę  .
.
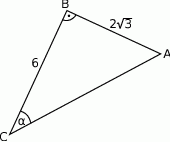
Zatem
A) 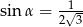 B)
B) 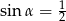 C)
C) 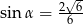 D)
D) 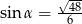
Dane są długości boków 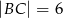 i
i 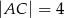 trójkąta prostokątnego
trójkąta prostokątnego 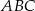 o kącie ostrym
o kącie ostrym 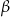 (zobacz rysunek).
(zobacz rysunek).
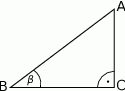
Wtedy
A) 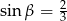 B)
B) 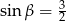 C)
C) 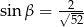 D)
D) 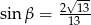
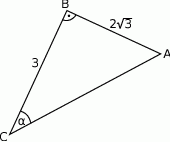
W trójkącie, przedstawionym na rysunku poniżej, cosinus kąta ostrego  jest równy
jest równy
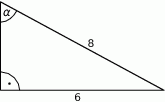
A)  B)
B)  C)
C) 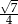 D)
D) 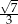
W trójkącie prostokątnym 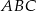 przyprostokątne mają długość
przyprostokątne mają długość 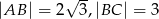 , a kąt
, a kąt  ma miarę
ma miarę  .
.
Zatem
A) 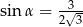 B)
B) 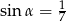 C)
C) 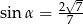 D)
D) 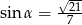
W trójkącie prostokątnym 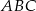 przyprostokątne mają długość
przyprostokątne mają długość 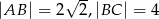 , a kąt
, a kąt 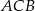 ma miarę
ma miarę  .
.
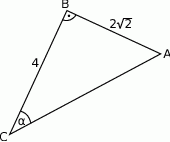
Zatem
A) 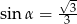 B)
B) 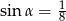 C)
C) 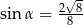 D)
D) 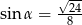
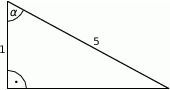
W trójkącie, przedstawionym na rysunku poniżej, sinus kąta ostrego  jest równy
jest równy
A) 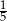 B)
B) 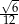 C)
C) 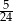 D)
D) 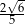
Pole trójkąta 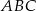 jest cztery razy mniejsze od pola trójkąta
jest cztery razy mniejsze od pola trójkąta 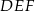 . Trójkąty te są podobne. Długość boku
. Trójkąty te są podobne. Długość boku 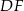 jest równa 16. Długość boku
jest równa 16. Długość boku 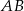 , odpowiadającego bokowi
, odpowiadającego bokowi 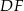 , jest równa
, jest równa
A) 64 B) 32 C) 4 D) 8
Trójkąty 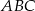 i
i 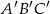 są podobne
są podobne 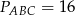 ,
, 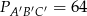 , wysokość
, wysokość 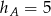 . Odpowiadająca jej wysokość w drugim trójkącie jest równa:
. Odpowiadająca jej wysokość w drugim trójkącie jest równa:
A) 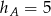 B)
B) 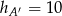 C)
C) 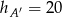 D) nie można określić
D) nie można określić
Pole trójkąta 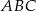 jest dziewięć razy mniejsze od pola trójkąta
jest dziewięć razy mniejsze od pola trójkąta 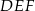 . Trójkąty te są podobne. Długość boku
. Trójkąty te są podobne. Długość boku 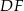 jest równa 9. Długość boku
jest równa 9. Długość boku 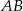 , odpowiadającego bokowi
, odpowiadającego bokowi 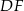 , jest równa
, jest równa
A) 81 B) 27 C) 3 D) 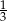
Pole trójkąta 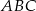 jest cztery razy większe od pola trójkąta
jest cztery razy większe od pola trójkąta 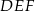 . Trójkąty te są podobne. Długość boku
. Trójkąty te są podobne. Długość boku 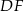 jest równa 16. Długość boku
jest równa 16. Długość boku 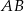 , odpowiadającego bokowi
, odpowiadającego bokowi 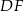 , jest równa
, jest równa
A) 64 B) 32 C) 4 D) 8
Wysokość trójkąta równobocznego o długości boku 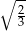 wynosi
wynosi
A) 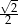 B)
B) 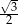 C)
C) 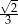 D)
D) 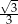
Pole koła opisanego na trójkącie równobocznym jest równe 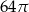 . Wysokość tego trójkąta ma długość
. Wysokość tego trójkąta ma długość
A) 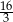 B) 16 C) 12 D) 24
B) 16 C) 12 D) 24

