Przyprostokątne trójkąta prostokątnego mają długości 1 i 7. Sinus najmniejszego kąta tego trójkąta jest równy
A) 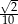 B)
B) 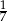 C)
C) 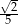 D)
D) 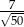
/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Trójkąt
Przyprostokątne trójkąta prostokątnego mają długości 8 i 6. Sinus większego z kątów ostrych tego trójkąta jest równy
A)  B)
B)  C)
C)  D)
D) 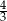
Przyprostokątne trójkąta prostokątnego mają długości 3 i 9. Sinus najmniejszego kąta tego trójkąta jest równy
A) 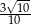 B)
B) 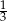 C)
C) 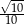 D)
D) 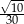
Przyprostokątne w trójkącie prostokątnym mają długości 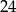 i
i 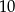 . Sinus najmniejszego kąta jest równy
. Sinus najmniejszego kąta jest równy
A) 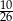 B)
B) 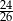 C)
C) 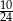 D)
D) 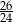
W trójkącie prostokątnym o długościach przyprostokątnych 2 i 5 cosinus większego z kątów ostrych jest równy
A)  B)
B)  C)
C) 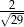 D)
D) 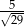
Przyprostokątne trójkąta prostokątnego mają długości 2 i 6. Sinus najmniejszego kąta tego trójkąta jest równy
A) 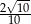 B)
B) 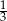 C)
C) 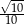 D)
D) 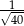
W trójkącie 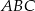 miary kątów wynoszą:
miary kątów wynoszą: 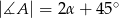 ,
, 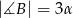 ,
, 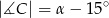 . Wówczas
. Wówczas
A) 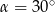 B)
B) 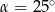 C)
C) 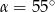 D)
D) 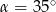
Stosunek długości podstawy do ramienia trójkąta równoramiennego jest równy 2:3. Ramię jest nachylone do podstawy pod kątem  , takim, że
, takim, że
A) 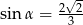 B)
B) 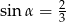 C)
C) 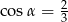 D)
D) 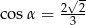
Stosunek długości podstawy do ramienia trójkąta równoramiennego jest równy 6:4. Ramię jest nachylone do podstawy pod kątem  , takim, że
, takim, że
A) 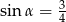 B)
B) 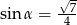 C)
C) 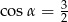 D)
D) 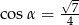
Stosunek długości podstawy do ramienia trójkąta równoramiennego jest równy 4:3. Ramię jest nachylone do podstawy pod kątem  , takim, że
, takim, że
A) 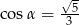 B)
B) 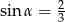 C)
C) 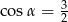 D)
D) 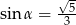
Dany jest trójkąt równoramienny 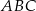 o kącie między ramionami
o kącie między ramionami 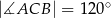 . Punkt
. Punkt 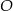 jest środkiem okręgu wpisanego w ten trójkąt. Prosta
jest środkiem okręgu wpisanego w ten trójkąt. Prosta 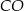 przecina podstawę
przecina podstawę 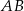 w punkcie
w punkcie 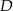 . Miara kąta
. Miara kąta 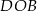 jest równa
jest równa
A) 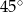 B)
B) 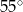 C)
C) 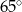 D)
D) 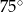
Dany jest trójkąt równoramienny 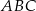 o kącie między ramionami
o kącie między ramionami 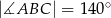 . Punkt
. Punkt 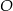 jest środkiem okręgu wpisanego w ten trójkąt. Prosta
jest środkiem okręgu wpisanego w ten trójkąt. Prosta 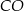 przecina podstawę
przecina podstawę 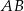 w punkcie
w punkcie 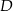 . Miara kąta
. Miara kąta 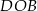 jest równa
jest równa
A) 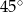 B)
B) 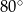 C)
C) 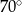 D)
D) 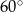
Dany jest trójkąt równoramienny 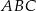 o kącie między ramionami
o kącie między ramionami 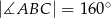 . Punkt
. Punkt 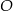 jest środkiem okręgu wpisanego w ten trójkąt. Prosta
jest środkiem okręgu wpisanego w ten trójkąt. Prosta 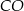 przecina podstawę
przecina podstawę 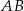 w punkcie
w punkcie 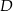 . Miara kąta
. Miara kąta 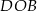 jest równa
jest równa
A) 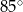 B)
B) 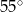 C)
C) 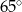 D)
D) 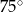
Pole trójkąta prostokątnego równoramiennego wynosi 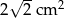 . Zatem przeciwprostokątna ma długość:
. Zatem przeciwprostokątna ma długość:
A) 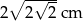 B)
B) 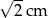 C)
C) 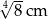 D)
D) 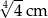
Pole trójkąta prostokątnego równoramiennego wynosi 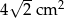 . Zatem przeciwprostokątna ma długość:
. Zatem przeciwprostokątna ma długość:
A) 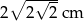 B)
B) 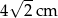 C)
C) 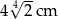 D)
D) 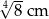
Pole trójkąta prostokątnego równoramiennego wynosi 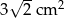 . Zatem przeciwprostokątna ma długość:
. Zatem przeciwprostokątna ma długość:
A) 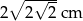 B)
B) 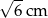 C)
C) 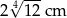 D)
D) 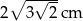
Pole trójkąta prostokątnego równoramiennego jest równe 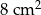 . Przeciwprostokątna tego trójkąta ma długość
. Przeciwprostokątna tego trójkąta ma długość
A) 8 cm B) 4 cm C) 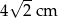 D)
D) 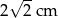
Przyprostokątna 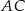 trójkąta prostokątnego
trójkąta prostokątnego 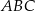 ma długość 6, a przeciwprostokątna
ma długość 6, a przeciwprostokątna 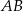 ma długość
ma długość 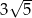 . Wtedy tangens kąta ostrego
. Wtedy tangens kąta ostrego 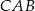 tego trójkąta jest równy
tego trójkąta jest równy
A) 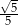 B)
B) 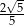 C)
C) 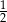 D) 2
D) 2
Kąt  jest kątem ostrym w trójkącie prostokątnym i
jest kątem ostrym w trójkącie prostokątnym i 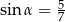 . Wówczas
. Wówczas
A) 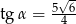 B)
B) 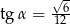 C)
C) 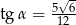 D)
D) 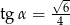
W trójkącie 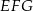 bok
bok 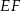 ma długość 21. Prosta równoległa do boku
ma długość 21. Prosta równoległa do boku 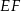 przecina boki
przecina boki 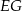 i
i 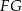 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 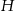 oraz
oraz 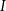 (zobacz rysunek) w taki sposób, że
(zobacz rysunek) w taki sposób, że 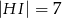 i
i 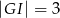 . Wtedy długość odcinka
. Wtedy długość odcinka 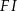 jest równa
jest równa
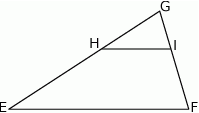
A) 6 B) 9 C) 12 D) 17
W trójkącie 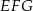 bok
bok 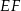 ma długość 24. Prosta równoległa do boku
ma długość 24. Prosta równoległa do boku 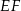 przecina boki
przecina boki 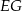 i
i 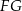 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 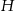 oraz
oraz 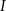 (zobacz rysunek) w taki sposób, że
(zobacz rysunek) w taki sposób, że 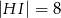 i
i 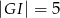 . Wtedy długość odcinka
. Wtedy długość odcinka 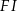 jest równa
jest równa
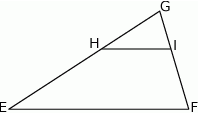
A) 6 B) 9 C) 10 D) 12
Ramię trójkąta równoramiennego 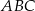 ma długość 8 cm i tworzy z podstawą kąt o mierze
ma długość 8 cm i tworzy z podstawą kąt o mierze 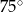 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 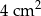 B)
B) 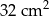 C)
C) 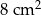 D)
D) 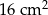
Dany jest trójkąt równoramienny, w którym ramię o długości 10 tworzy z podstawą kąt 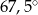 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 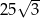 B)
B) 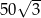 C)
C) 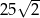 D)
D) 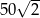
Dany jest trójkąt równoramienny, w którym ramię o długości 20 tworzy z podstawą kąt 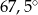 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 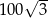 B)
B) 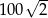 C)
C) 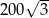 D)
D) 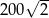
w trójkącie równoramiennym ramię ma długość 16 i tworzy z podstawą trójkąta kąt o mierze 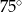 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 128 B) 64 C) 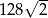 D)
D) 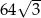
Przez punkt przecięcia wysokości trójkąta równobocznego 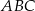 poprowadzono prostą
poprowadzono prostą 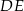 równoległą do podstawy
równoległą do podstawy 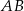 (zobacz rysunek).
(zobacz rysunek).
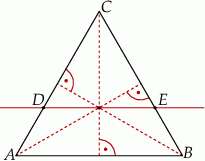
Stosunek pola trójkąta 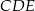 do pola trapezu
do pola trapezu 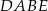 jest równy
jest równy
A) 5 : 9 B) 4 : 5 C) 4 : 9 D) 3 : 2
Dany jest trójkąt równoboczny 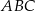 o boku długości 8. Ze środka
o boku długości 8. Ze środka 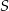 boku
boku 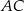 zakreślono koło o promieniu równym połowie boku trójkąta (zobacz rysunek).
zakreślono koło o promieniu równym połowie boku trójkąta (zobacz rysunek).
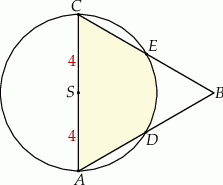
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Krótsze z łuków wyciętych przez punkty 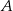 i i 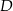 , oraz , oraz 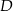 i i 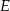 z danego okręgu, mają tą samą długość. z danego okręgu, mają tą samą długość. | P | F |
Odcinek 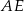 jest dwa razy dłuższy od odcinka jest dwa razy dłuższy od odcinka 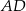 . . | P | F |
Odcinki 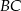 i
i 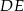 są równoległe i
są równoległe i 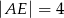 ,
, 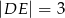 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 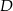 jest środkiem odcinka
jest środkiem odcinka 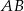 . Długość odcinka
. Długość odcinka 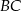 jest równa
jest równa
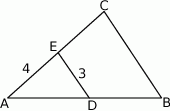
A) 4 B) 6 C) 8 D) 16
Odcinki 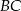 i
i 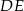 są równoległe i
są równoległe i 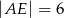 ,
, 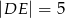 (zobacz rysunek). Punkt
(zobacz rysunek). Punkt 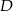 jest środkiem odcinka
jest środkiem odcinka 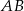 . Długość odcinka
. Długość odcinka 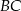 jest równa
jest równa
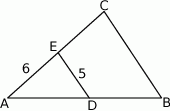
A) 10 B) 6 C) 8 D) 30
W trójkącie prostokątnym o przyprostokątnych 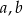 oraz przeciwprostokątnej
oraz przeciwprostokątnej  , kąt
, kąt  znajduje się naprzeciw przyprostokątnej
znajduje się naprzeciw przyprostokątnej  .
.
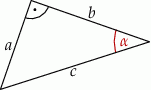
Wiadomo, że cosinus kąta  jest równy
jest równy  . Wyrażenie
. Wyrażenie 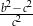 ma wartość:
ma wartość:
A) 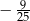 B)
B) 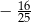 C)
C) 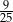 D)
D) 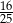
Długości boków trójkąta 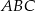 są równe 10 cm, 11 cm, 15 cm. Zatem
są równe 10 cm, 11 cm, 15 cm. Zatem
A) trójkąt ten jest ostrokątny
B) trójkąt ten jest prostokątny
C) trójkąt ten jest rozwartokątny
D) jest zbyt mało danych aby określić jakiego rodzaju jest to trójkąt
Długości boków trójkąta 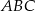 są równe 8 cm, 15 cm, 17 cm. Zatem
są równe 8 cm, 15 cm, 17 cm. Zatem
A) trójkąt ten jest ostrokątny
B) trójkąt ten jest prostokątny
C) trójkąt ten jest rozwartokątny
D) jest zbyt mało danych aby określić jakiego rodzaju jest to trójkąt
Długości boków trójkąta 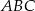 są równe 10 cm, 12 cm, 15 cm. Zatem
są równe 10 cm, 12 cm, 15 cm. Zatem
A) trójkąt ten jest ostrokątny
B) trójkąt ten jest prostokątny
C) trójkąt ten jest rozwartokątny
D) jest zbyt mało danych aby określić jakiego rodzaju jest to trójkąt
Promień koła wpisanego w trójkąt prostokątny o bokach 5 cm, 12 cm, 13 cm ma długość
A) 2,2 cm B) 1,8 cm C) 1,5 cm D) 2 cm
Promień koła wpisanego w trójkąt prostokątny o bokach 6 cm, 8 cm, 10 cm ma długość
A) 2,2 cm B) 2 cm C) 1,5 cm D) 1,8 cm
Promień koła wpisanego w trójkąt prostokątny o bokach 8 cm, 15 cm, 17 cm ma długość
A) 3 cm B) 1,8 cm C) 1,5 cm D) 2 cm
Dwusieczne kątów ostrych trójkąta prostokątnego 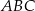 przecinają się w punkcie
przecinają się w punkcie 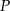 . Przyprostokątne
. Przyprostokątne 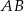 i
i 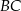 mają długości równe odpowiednio 12 i 9 (zobacz rysunek).
mają długości równe odpowiednio 12 i 9 (zobacz rysunek).
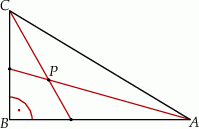
Odległość punktu 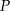 od przeciwprostokątnej
od przeciwprostokątnej 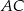 jest równa
jest równa
A) 3 B) 2 C) 15 D) 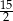
Dany jest trójkąt prostokątny 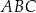 o bokach
o bokach 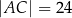 ,
, 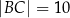 ,
, 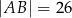 . Dwusieczne kątów tego trójkąta przecinają się w punkcie
. Dwusieczne kątów tego trójkąta przecinają się w punkcie 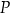 (zobacz rysunek).
(zobacz rysunek).
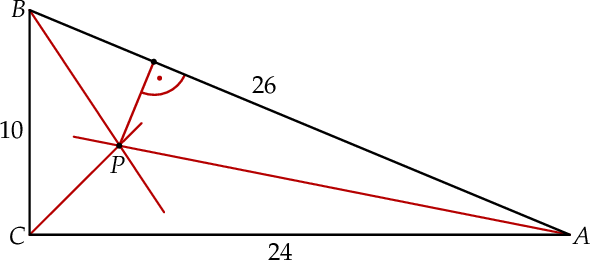
Odległość  punktu
punktu 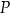 od przeciwprostokątnej
od przeciwprostokątnej 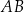 jest równa
jest równa
A) 2 B) 4 C)  D)
D) 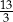
Dany jest trójkąt prostokątny 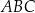 o bokach
o bokach 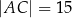 ,
, 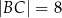 ,
, 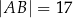 . Dwusieczne kątów tego trójkąta przecinają się w punkcie
. Dwusieczne kątów tego trójkąta przecinają się w punkcie 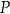 (zobacz rysunek).
(zobacz rysunek).

Odległość  punktu
punktu 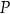 od przeciwprostokątnej
od przeciwprostokątnej 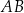 jest równa
jest równa
A) 2 B) 4 C)  D) 3
D) 3
Dany jest trójkąt prostokątny 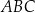 o bokach
o bokach 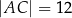 ,
, 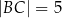 ,
, 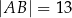 . Dwusieczne kątów tego trójkąta przecinają się w punkcie
. Dwusieczne kątów tego trójkąta przecinają się w punkcie 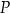 (zobacz rysunek).
(zobacz rysunek).

Odległość  punktu
punktu 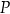 od przeciwprostokątnej
od przeciwprostokątnej 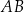 jest równa
jest równa
A) 1 B) 2 C)  D)
D) 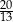
Dany jest trójkąt równoboczny 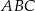 o boku długości 8. Ze środka
o boku długości 8. Ze środka 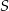 boku
boku 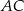 zakreślono koło o promieniu równym połowie boku trójkąta (zobacz rysunek).
zakreślono koło o promieniu równym połowie boku trójkąta (zobacz rysunek).
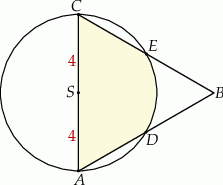
Pole powierzchni części wspólnej koła i trójkąta jest równe
A) 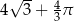 B)
B) 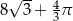 C)
C) 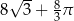 D)
D) 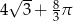
Wysokość trójkąta równobocznego jest równa 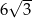 . Pole tego trójkąta jest równe
. Pole tego trójkąta jest równe
A) 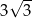 B)
B) 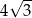 C)
C) 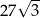 D)
D) 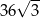
Pole trójkąta równobocznego o wysokości 3 jest równe
A) 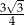 B)
B) 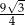 C)
C) 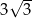 D)
D) 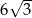
Trójkąt 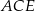 jest prostokątny oraz
jest prostokątny oraz 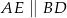 (zobacz rysunek).
(zobacz rysunek).
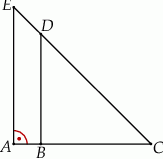
Jeżeli 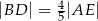 oraz
oraz 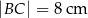 , to
, to
A) 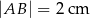 B)
B) 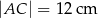 C)
C) 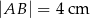 D)
D) 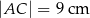
Dany jest trójkąt 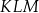 , w którym
, w którym 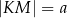 ,
, 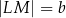 oraz
oraz 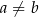 . Dwusieczna kąta
. Dwusieczna kąta 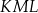 przecina bok
przecina bok 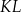 w punkcie
w punkcie 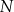 takim, że
takim, że 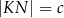 ,
, 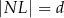 oraz
oraz 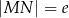 (zobacz rysunek).
(zobacz rysunek).

W trójkącie 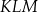 prawdziwa jest równość
prawdziwa jest równość
A) 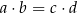 B)
B) 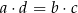 C)
C) 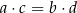 D)
D)