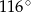Miara kąta  wynosi
wynosi
A) 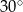 B)
B) 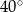 C)
C) 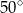 D)
D) 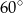
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Miara kąta  wynosi
wynosi

A) 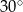 B)
B) 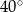 C)
C) 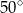 D)
D) 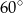
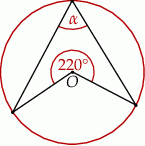
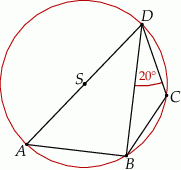
Punkty 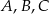 i
i 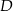 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 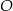 . Cięciwy
. Cięciwy 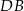 i
i 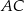 przecinają się w punkcie
przecinają się w punkcie 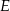 ,
, 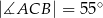 oraz
oraz 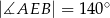 (zobacz rysunek).
(zobacz rysunek).
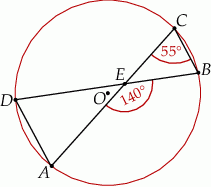
Miara kąta 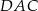 jest równa
jest równa
A) 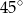 B)
B) 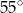 C)
C) 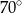 D)
D) 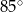
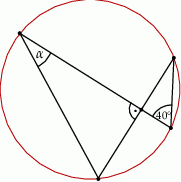
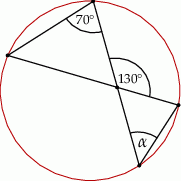
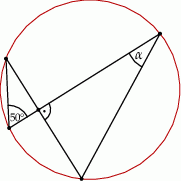
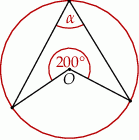
Kąt  na rysunku obok ma miarę
na rysunku obok ma miarę
A) 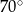 B)
B) 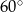 C)
C) 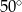 D)
D) 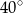
Miara kąta  wynosi
wynosi
A) 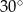 B)
B) 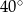 C)
C) 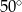 D)
D) 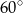
Miara kąta  wynosi
wynosi
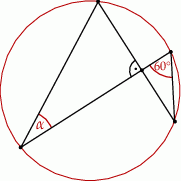
A) 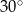 B)
B) 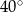 C)
C) 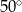 D)
D) 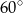
Punkty 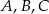 i
i 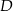 leżą na okręgu o środku w punkcie
leżą na okręgu o środku w punkcie 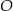 . Cięciwy
. Cięciwy 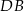 i
i 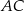 przecinają się w punkcie
przecinają się w punkcie 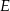 ,
, 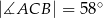 oraz
oraz 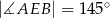 (zobacz rysunek).
(zobacz rysunek).
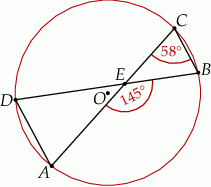
Miara kąta 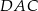 jest równa
jest równa
A) 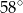 B)
B) 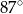 C)
C) 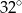 D)
D) 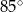
Punkty  leżą na okręgu o środku
leżą na okręgu o środku  (zobacz rysunek). Miara zaznaczonego kąta
(zobacz rysunek). Miara zaznaczonego kąta  jest równa
jest równa
A) 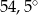 B)
B) 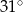 C)
C) 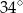 D)
D) 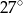
Punkty 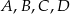 leżą na okręgu o środku
leżą na okręgu o środku  (zobacz rysunek). Miara zaznaczonego kąta
(zobacz rysunek). Miara zaznaczonego kąta  jest równa
jest równa
A) 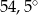 B)
B) 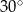 C)
C) 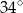 D)
D) 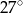
Punkty 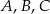 i
i 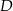 leżą na okręgu o środku
leżą na okręgu o środku 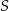 . Miary kątów
. Miary kątów 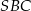 ,
, 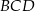 ,
, 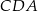 są równe odpowiednio:
są równe odpowiednio: 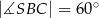 ,
, 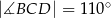 ,
, 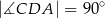 (zobacz rysunek).
(zobacz rysunek).
Wynika stąd, że miara  kąta
kąta 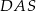 jest równa
jest równa
A) 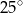 B)
B) 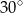 C)
C) 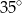 D)
D) 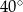
Punkty 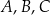 i
i 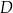 leżą na okręgu o środku
leżą na okręgu o środku 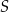 . Miary kątów
. Miary kątów 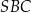 ,
, 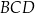 ,
, 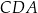 są równe odpowiednio:
są równe odpowiednio: 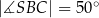 ,
,  ,
,  (zobacz rysunek).
(zobacz rysunek).
Wynika stąd, że miara  kąta
kąta 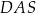 jest równa
jest równa
A) 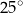 B)
B) 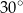 C)
C) 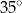 D)
D) 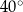
Punkty 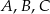 i
i 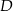 leżą na okręgu o środku
leżą na okręgu o środku 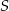 . Miary kątów
. Miary kątów 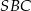 ,
,  ,
,  są równe odpowiednio:
są równe odpowiednio:  ,
, 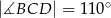 ,
, 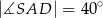 (zobacz rysunek).
(zobacz rysunek).
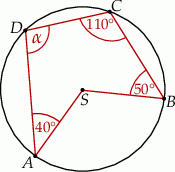
Wynika stąd, że miara  kąta
kąta  jest równa
jest równa
A) 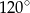 B)
B) 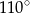 C)
C) 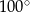 D)
D) 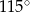
Punkty 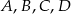 dzielą okrąg na 4 równe łuki. Miara zaznaczonego na rysunku kąta wpisanego
dzielą okrąg na 4 równe łuki. Miara zaznaczonego na rysunku kąta wpisanego 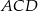 jest równa
jest równa
A) 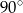 B)
B) 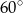 C)
C) 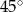 D)
D) 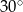
Punkt 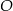 jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy 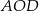 ma miarę
ma miarę
A)  B)
B)  C)
C) 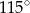 D)
D) 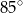
Punkt 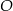 jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy 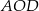 ma miarę
ma miarę
A) 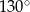 B)
B) 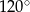 C)
C) 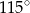 D)
D) 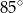
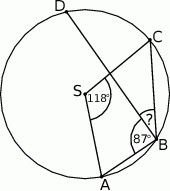
Punkty 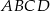 leżą na okręgu o środku
leżą na okręgu o środku 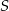 (zobacz rysunek). Miara kąta
(zobacz rysunek). Miara kąta 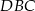 jest równa
jest równa
A) 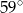 B)
B) 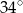 C)
C) 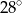 D)
D) 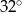
Punkt  jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  przedstawiony na rysunku ma miarę:
przedstawiony na rysunku ma miarę:
A) 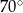 B)
B) 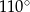 C)
C) 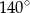 D)
D) 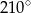
Punkt 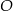 jest środkiem okręgu. Kąt wpisany
jest środkiem okręgu. Kąt wpisany  przedstawiony na rysunku ma miarę:
przedstawiony na rysunku ma miarę:
A) 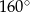 B)
B) 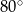 C)
C) 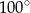 D)
D) 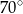
Miara kąta  (patrz rysunek obok) jest równa
(patrz rysunek obok) jest równa
A) 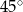 B)
B) 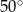 C)
C) 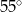 D)
D) 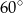
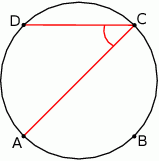
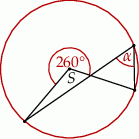
Na trójkącie 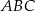 opisano okrąg i poprowadzono styczną do okręgu w punkcie
opisano okrąg i poprowadzono styczną do okręgu w punkcie 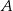 (zobacz rysunek obok).
(zobacz rysunek obok).
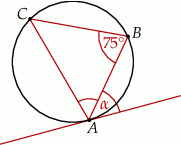
Jeżeli 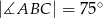 i kąt dopisany
i kąt dopisany  jest równy
jest równy 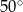 , to kąt
, to kąt 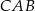 ma miarę:
ma miarę:
A) 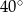 B)
B) 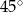 C)
C) 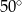 D)
D) 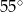
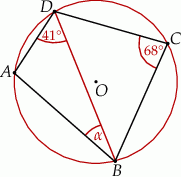
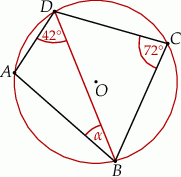
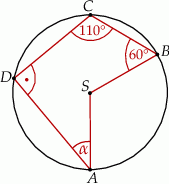
Czworokąt 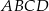 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 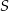 . Bok
. Bok 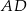 jest średnicą tego okręgu, a miara kąta
jest średnicą tego okręgu, a miara kąta 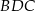 jest równa
jest równa 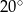 (zobacz rysunek).
(zobacz rysunek).
Wtedy miara kąta  jest równa
jest równa
A) 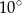 B)
B) 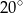 C)
C) 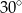 D)
D) 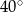
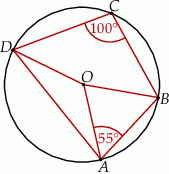
Czworokąt 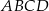 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku 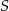 . Bok
. Bok 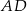 jest średnicą tego okręgu, a miara kąta
jest średnicą tego okręgu, a miara kąta 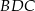 jest równa
jest równa 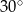 (zobacz rysunek).
(zobacz rysunek).
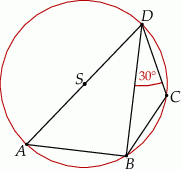
Wtedy miara kąta 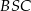 jest równa
jest równa
A) 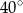 B)
B) 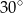 C)
C) 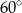 D)
D) 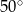
Cięciwy 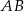 i
i 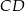 okręgu o środku
okręgu o środku 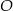 przecinają się w punkcie
przecinają się w punkcie 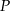 i tworzą trójkąty
i tworzą trójkąty 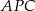 i
i 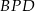 .
.
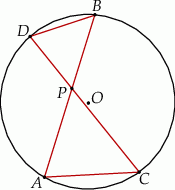
Trójkąty 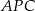 i
i 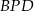 są
są
| A) podobne, | B) przystające, |
ponieważ trójkąty te mają równe
| 1) pola, | 2) miary kątów, | 3) długości boków, |
Odcinek 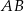 jest średnicą okręgu (rysunek).
jest średnicą okręgu (rysunek).
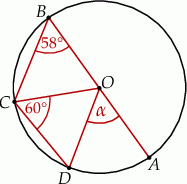
Miara kąta  jest równa
jest równa
A) 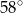 B)
B) 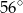 C)
C) 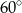 D)
D)