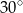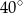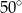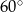Na rysunku przedstawiono trzy figury. Figura 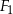 powstała z koła o promieniu
powstała z koła o promieniu 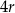 , z którego wycięto wnętrza czterech kół o promieniu
, z którego wycięto wnętrza czterech kół o promieniu  . Figura
. Figura 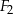 składa się z dwóch stycznych zewnętrznie kół o promieniach
składa się z dwóch stycznych zewnętrznie kół o promieniach 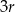 i
i 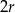 . Figura
. Figura 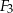 powstała z koła o promieniu
powstała z koła o promieniu 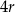 , z którego wycięto wnętrza dwóch kół o promieniu
, z którego wycięto wnętrza dwóch kół o promieniu 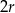 .
.
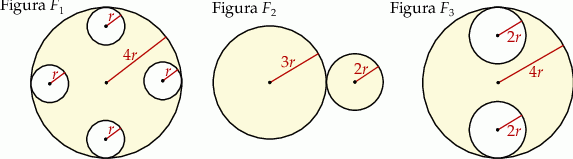
Jeżeli  ,
,  i
i  oznaczają pola figur odpowiednio
oznaczają pola figur odpowiednio 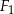 ,
, 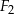 i
i 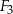 , to
, to
A) 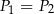 i
i 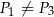 B)
B) 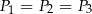
C) 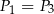 i
i 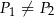 D)
D) 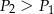

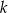 jest styczna do okręgu o promieniu 3 w punkcie
jest styczna do okręgu o promieniu 3 w punkcie 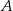 i jest styczna do okręgu o promieniu 4 w punkcie
i jest styczna do okręgu o promieniu 4 w punkcie 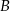 (zobacz rysunek).
(zobacz rysunek). 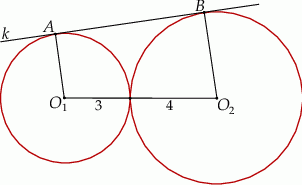
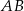 jest równa
jest równa 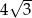
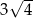
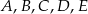 dzielą okrąg na 5 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego
dzielą okrąg na 5 równych łuków. Miara zaznaczonego na rysunku kąta wpisanego 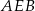 jest równa
jest równa 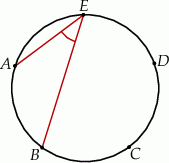
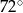
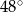
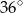
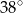
 okręgu są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego
okręgu są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego 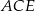 jest równa
jest równa 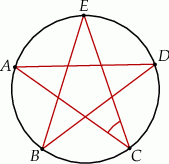
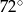
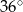
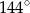
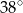
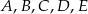 leżące na okręgu o środku
leżące na okręgu o środku 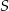 są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego
są wierzchołkami pięciokąta foremnego. Miara zaznaczonego na rysunku kąta wpisanego 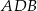 jest równa
jest równa 
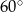
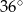
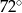
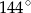
 i
i  leżą na okręgu o środku
leżą na okręgu o środku  (zobacz rysunek).
(zobacz rysunek). 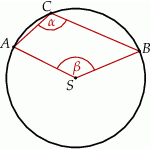
 i
i  zaznaczonych kątów
zaznaczonych kątów  i
i 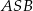 spełniają warunek
spełniają warunek 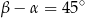 . Wynika stąd, że
. Wynika stąd, że 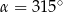
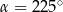
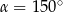
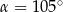
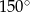
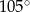
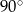
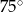
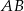 i
i 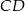 okręgu o środku
okręgu o środku 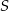 przecinają się pod kątem
przecinają się pod kątem 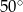 (tak jak na rysunku).
(tak jak na rysunku). 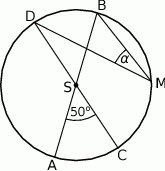
 jest równa
jest równa 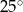
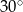
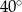
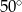
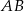 i
i 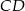 okręgu o środku
okręgu o środku 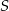 przecinają się pod kątem
przecinają się pod kątem 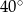 (tak jak na rysunku).
(tak jak na rysunku). 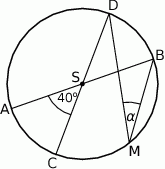
 jest równa
jest równa 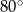
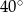
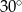
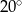
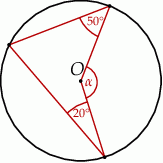
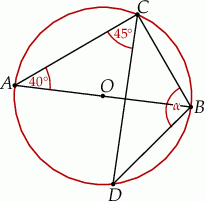
 jest środkiem okręgu. Kąt
jest środkiem okręgu. Kąt  , zaznaczony na rysunku, ma miarę
, zaznaczony na rysunku, ma miarę 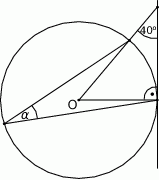
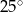
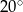
 jest środkiem okręgu. Kąt
jest środkiem okręgu. Kąt  , zaznaczony na rysunku, ma miarę
, zaznaczony na rysunku, ma miarę 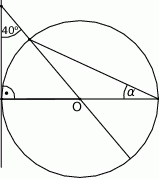
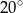
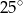
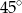
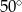
 jest środkiem okręgu (zobacz rysunek). Miara kąta
jest środkiem okręgu (zobacz rysunek). Miara kąta  jest równa
jest równa 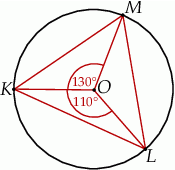
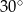
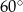
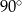
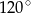
 jest równa
jest równa 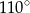
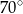
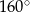
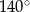
 jest środkiem okręgu (rysunek).
jest środkiem okręgu (rysunek). 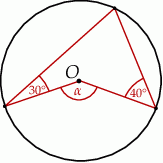
 jest równa
jest równa 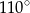
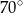
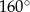
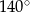
 leżą na okręgu o środku
leżą na okręgu o środku  (zobacz rysunek). Ponadto
(zobacz rysunek). Ponadto 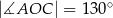 oraz
oraz  .
. 
 trójkąta
trójkąta 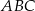 jest równa
jest równa 
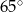
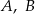 i
i 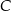 leżą na okręgu o środku
leżą na okręgu o środku 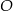 (zobacz rysunek). Zaznaczony na rysunku wypukły kąt środkowy
(zobacz rysunek). Zaznaczony na rysunku wypukły kąt środkowy 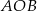 ma miarę
ma miarę 
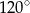
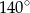
 leżą na okręgu o środku
leżą na okręgu o środku 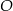 (zobacz rysunek). Ponadto
(zobacz rysunek). Ponadto 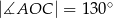 oraz
oraz 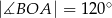 .
. 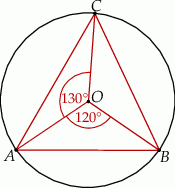
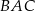 trójkąta
trójkąta 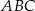 jest równa
jest równa 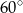
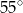
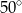
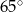
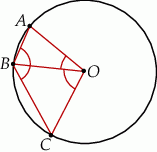
 leżą punkty
leżą punkty  i
i  (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 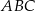 ma miarę
ma miarę 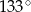 , a kąt
, a kąt 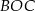 ma miarę
ma miarę 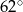 .
. 
 ma miarę
ma miarę 
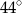
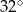
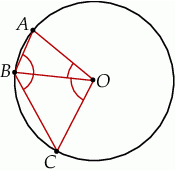
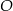 leżą punkty
leżą punkty 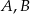 i
i 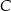 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 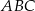 ma miarę
ma miarę 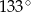 , a kąt
, a kąt 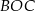 ma miarę
ma miarę 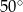 .
. 
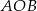 ma miarę
ma miarę 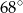
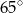
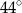
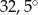
 jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy  ma miarę
ma miarę 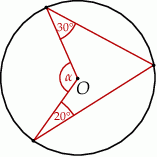
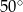
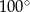
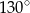
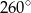
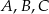 leżą na okręgu o środku
leżą na okręgu o środku 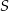 (rysunek),
(rysunek), 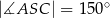 oraz
oraz 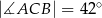 . Miara kąta
. Miara kąta 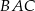 jest równa
jest równa 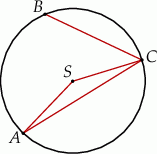
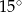
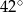
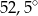
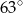
 leżą punkty
leżą punkty 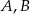 i
i 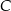 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 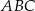 ma miarę
ma miarę 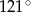 , a kąt
, a kąt 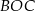 ma miarę
ma miarę 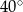 .
. 
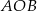 ma miarę
ma miarę 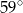
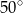
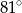
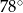
 trójkąta prostokątnego
trójkąta prostokątnego  poprowadzono styczną do okręgu opisanego na tym trójkącie.
poprowadzono styczną do okręgu opisanego na tym trójkącie. 
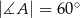 to miara kąta
to miara kąta  jest równa
jest równa 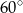
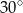
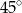
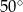
 trójkąta prostokątnego
trójkąta prostokątnego  poprowadzono styczną do okręgu opisanego na tym trójkącie.
poprowadzono styczną do okręgu opisanego na tym trójkącie. 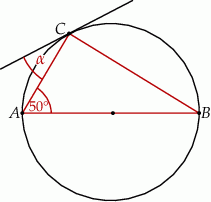
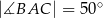 to miara kąta
to miara kąta  jest równa
jest równa 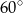
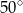
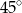
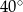
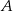 . Punkty
. Punkty 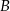 i
i 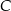 są położone na okręgu tak, że
są położone na okręgu tak, że 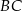 jest jego średnicą. Cięciwa
jest jego średnicą. Cięciwa 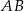 tworzy ze styczną kąt o mierze
tworzy ze styczną kąt o mierze 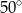 (zobacz rysunek).
(zobacz rysunek). 
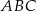 jest równa
jest równa 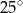
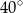
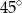
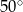
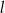 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 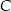 . Jeżeli kąt
. Jeżeli kąt 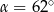 , to miara kąta
, to miara kąta 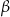 jest równa
jest równa 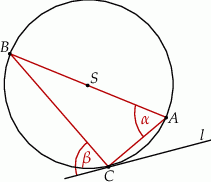
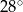
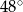
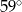
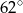
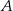 . Punkty
. Punkty 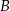 i
i 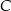 są położone na okręgu tak, że
są położone na okręgu tak, że 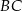 jest jego średnicą. Cięciwa
jest jego średnicą. Cięciwa 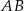 tworzy ze styczną kąt o mierze
tworzy ze styczną kąt o mierze 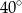 (zobacz rysunek).
(zobacz rysunek). 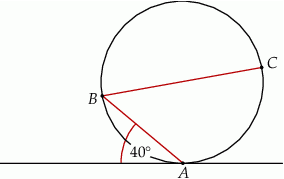
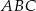 jest równa
jest równa 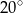
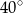
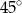
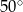
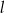 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 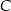 . Jeżeli kąt
. Jeżeli kąt 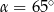 , to miara kąta
, to miara kąta 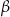 jest równa
jest równa 
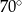
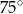
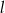 jest styczna do okręgu o środku
jest styczna do okręgu o środku 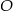 w punkcie
w punkcie 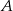 ,
, 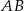 jest cięciwą okręgu,
jest cięciwą okręgu, 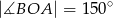 . Wówczas kąt ostry
. Wówczas kąt ostry  między cięciwą
między cięciwą 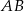 , a prostą
, a prostą 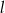 jest równy
jest równy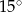
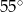
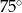
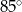
 poprowadzono cięciwę
poprowadzono cięciwę  . Trójkąt
. Trójkąt  jest prostokątny. Miara kąta, jaki tworzy cięciwa
jest prostokątny. Miara kąta, jaki tworzy cięciwa 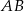 ze styczną do okręgu poprowadzoną w punkcie
ze styczną do okręgu poprowadzoną w punkcie 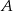 , jest równa
, jest równa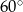
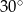
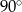
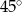
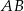 jest średnicą okręgu o środku
jest średnicą okręgu o środku 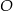 .
. 
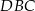 oznaczonego na rysunku literą
oznaczonego na rysunku literą  jest równa
jest równa 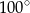
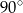
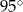
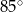
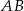 jest średnicą okręgu o środku
jest średnicą okręgu o środku 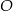 .
. 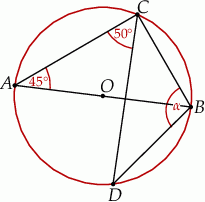
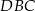 oznaczonego na rysunku literą
oznaczonego na rysunku literą  jest równa
jest równa 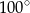
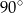
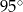
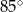
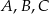 i
i 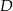 leżą na okręgu o środku
leżą na okręgu o środku 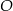 . Punkt
. Punkt  leży na odcinku
leży na odcinku 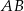 oraz
oraz 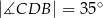 ,
, 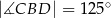 .
. 
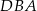 oznaczonego na rysunku literą
oznaczonego na rysunku literą  jest równa
jest równa 
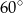
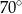
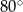
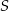 . Punkty
. Punkty 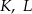 i
i 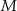 leżą na tym okręgu. Na łuku
leżą na tym okręgu. Na łuku 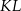 tego okręgu są oparte kąty
tego okręgu są oparte kąty 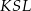 i
i 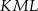 (zobacz rysunek), których miary
(zobacz rysunek), których miary  i
i  spełniają warunek
spełniają warunek 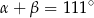 . Wynika stąd, że
. Wynika stąd, że 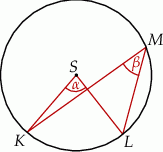
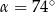
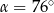
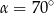
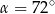
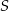 . Punkty
. Punkty 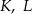 i
i 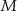 leżą na tym okręgu. Na łuku
leżą na tym okręgu. Na łuku 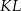 tego okręgu są oparte kąty
tego okręgu są oparte kąty 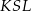 i
i 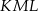 (zobacz rysunek), których miary
(zobacz rysunek), których miary  i
i 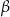 spełniają warunek
spełniają warunek 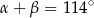 . Wynika stąd, że
. Wynika stąd, że 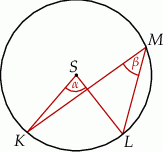
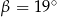
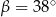
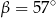
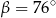
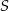 . Punkty
. Punkty 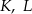 i
i 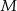 leżą na tym okręgu. Na łuku
leżą na tym okręgu. Na łuku 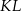 tego okręgu są oparte kąty
tego okręgu są oparte kąty 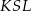 i
i 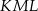 (zobacz rysunek), których miary
(zobacz rysunek), których miary  i
i 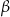 spełniają warunek
spełniają warunek 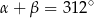 . Wynika stąd, że
. Wynika stąd, że 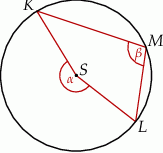
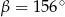
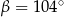
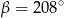
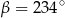
 . Punkty
. Punkty  i
i 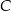 leżą na tym okręgu. Na łuku
leżą na tym okręgu. Na łuku 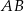 tego okręgu są oparte kąty
tego okręgu są oparte kąty 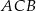 i
i 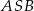 (zobacz rysunek), których miary
(zobacz rysunek), których miary  i
i 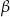 spełniają warunek
spełniają warunek 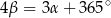 . Wynika stąd, że
. Wynika stąd, że 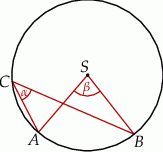
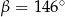
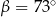
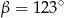
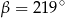
 kąt środkowy
kąt środkowy 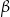 jest oparty na łuku trzy razy dłuższym od łuku, na którym oparty jest kąt wpisany
jest oparty na łuku trzy razy dłuższym od łuku, na którym oparty jest kąt wpisany  . Kąt
. Kąt 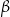 ma miarę o
ma miarę o 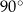 większą od kąta
większą od kąta  . Miara kąta
. Miara kąta 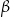 jest równa
jest równa 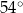
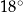
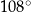
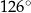
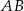 jest średnicą okręgu o środku
jest średnicą okręgu o środku 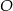 i promieniu
i promieniu  . Na tym okręgu wybrano punkt
. Na tym okręgu wybrano punkt 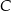 , taki, że
, taki, że 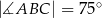 (zobacz rysunek).
(zobacz rysunek). 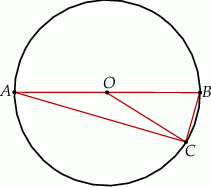
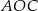 jest równe
jest równe 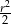
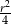
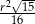
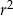
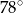 jest równa
jest równa 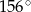
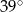
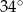
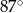
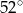 jest równa
jest równa 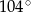
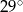
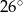
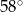
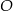 jest środkiem okręgu.
jest środkiem okręgu. 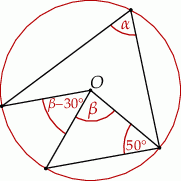
 jest równa
jest równa 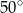
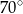
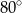
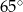
 jest środkiem okręgu.
jest środkiem okręgu. 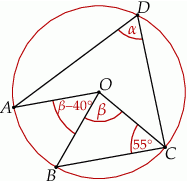
 jest równa
jest równa 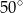
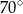
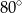
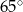
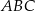 jest wpisany w okrąg o środku
jest wpisany w okrąg o środku  . Jeśli
. Jeśli 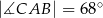 i
i 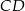 jest średnicą okręgu, to miara kąta
jest średnicą okręgu, to miara kąta 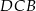 jest równa
jest równa 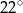
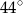
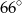
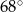
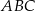 (patrz rysunek) ma miarę
(patrz rysunek) ma miarę 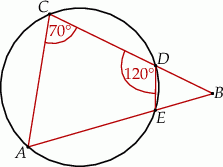
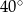
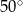
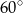
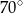
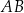 i
i 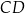 okręgu są oparte kąty wpisane
okręgu są oparte kąty wpisane 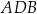 i
i 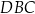 , takie, że
, takie, że 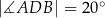 i
i 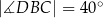 (zobacz rysunek). Cięciwy
(zobacz rysunek). Cięciwy 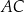 i
i 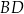 przecinają się w punkcie
przecinają się w punkcie 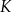 .
. 
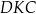 jest równa
jest równa 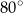
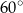
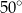
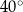
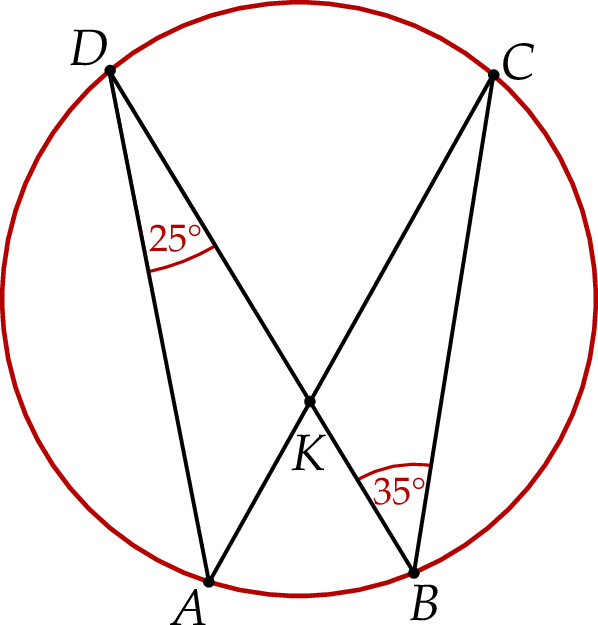
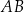 i
i 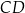 okręgu są oparte kąty wpisane
okręgu są oparte kąty wpisane 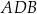 i
i 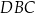 , takie, że
, takie, że 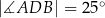 i
i 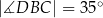 (zobacz rysunek). Cięciwy
(zobacz rysunek). Cięciwy 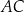 i
i 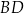 przecinają się w punkcie
przecinają się w punkcie 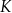 .
. 
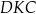 jest równa
jest równa 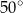
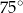
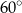
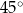
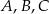 czworokąta
czworokąta 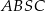 leżą na okręgu o środku
leżą na okręgu o środku 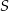 . Kąt
. Kąt 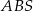 ma miarę
ma miarę 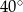 (zobacz rysunek), a przekątna
(zobacz rysunek), a przekątna  jest dwusieczną tego kąta.
jest dwusieczną tego kąta. 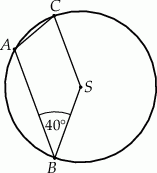
 jest równa
jest równa