Wykres funkcji 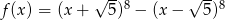 przecina oś
przecina oś 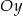 w punkcie
w punkcie
A) 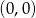 B)
B) 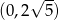 C)
C) 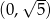 D)
D) 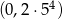
/Szkoła średnia/Zadania testowe/Funkcje/Wielomiany
Wykres funkcji 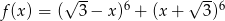 przecina oś
przecina oś 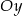 w punkcie
w punkcie
A) 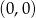 B)
B) 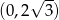 C)
C) 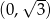 D)
D) 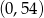
Wykres funkcji 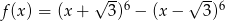 przecina oś
przecina oś 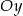 w punkcie
w punkcie
A) 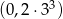 B)
B) 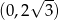 C)
C) 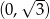 D)
D) 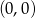
Wielomian 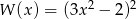 jest równy wielomianowi
jest równy wielomianowi
A) 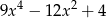 B)
B) 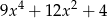 C)
C) 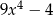 D)
D) 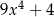
Wielomian 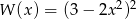 jest równy wielomianowi
jest równy wielomianowi
A) 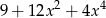 B)
B) 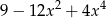 C)
C) 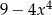 D)
D) 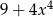
Wielomian 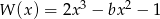 jest podzielny przez dwumian
jest podzielny przez dwumian 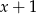 . Wynika stąd, że
. Wynika stąd, że
A) 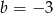 B)
B) 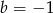 C)
C) 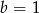 D)
D) 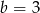
Wielomian 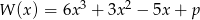 jest podzielny przez dwumian
jest podzielny przez dwumian 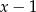 dla
dla 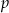 równego
równego
A) 4 B) 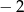 C) 2 D)
C) 2 D) 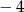
Wielomian 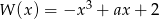 jest podzielny przez dwumian
jest podzielny przez dwumian 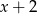 . Wynika stąd, że
. Wynika stąd, że
A) 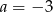 B)
B) 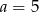 C)
C) 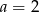 D)
D) 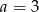
Wielomian 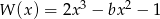 jest podzielny przez dwumian
jest podzielny przez dwumian 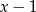 . Wynika stąd, że
. Wynika stąd, że
A) 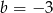 B)
B) 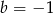 C)
C) 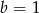 D)
D) 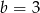
Reszta z dzielenia wielomianu 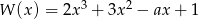 przez dwumian
przez dwumian 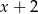 jest równa
jest równa 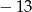 . Zatem
. Zatem
A) 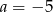 B)
B) 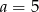 C)
C) 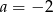 D)
D) 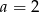
Reszta z dzielenia wielomianu 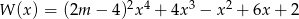 przez dwumian
przez dwumian 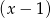 jest równa 11 dla
jest równa 11 dla
A) 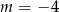 B)
B) 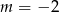 C)
C) 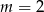 D)
D) 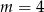
Reszta z dzielenia wielomianu 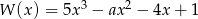 przez dwumian
przez dwumian 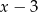 jest równa 88. Zatem
jest równa 88. Zatem
A) 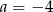 B)
B) 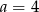 C)
C) 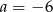 D)
D) 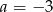
Dane są wielomiany 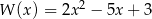 i
i 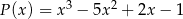 . Wielomian
. Wielomian 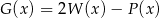 jest równy
jest równy
A) 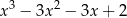 B)
B) 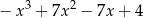
C) 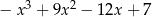 D)
D) 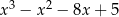
Dane są wielomiany 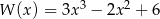 oraz
oraz 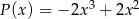 . Wielomian
. Wielomian 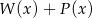 jest równy
jest równy
A) 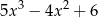 B)
B) 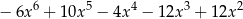
C) 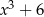 D)
D) 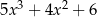
Dane są wielomiany 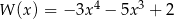 oraz
oraz 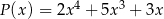 . Wielomian
. Wielomian 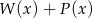 jest równy
jest równy
A) 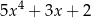 B)
B) 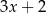
C) 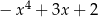 D)
D) 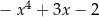
Dane są wielomiany 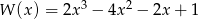 i
i 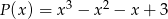 . Wielomian
. Wielomian 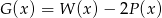 jest równy
jest równy
A) 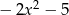 B)
B) 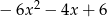 C)
C) 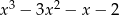 D)
D) 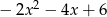
Dane są wielomiany 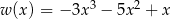 i
i 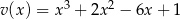 . Wówczas wielomian
. Wówczas wielomian 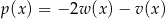 jest równy:
jest równy:
A) 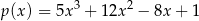 B)
B) 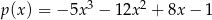
C) 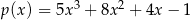 D)
D) 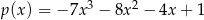
Dane są wielomiany 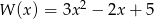 oraz
oraz 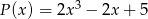 . Wielomian
. Wielomian 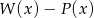 jest równy
jest równy
A) 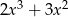 B)
B) 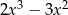 C)
C) 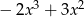 D)
D) 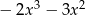
Dane są wielomiany 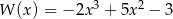 oraz
oraz 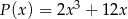 . Wielomian
. Wielomian 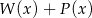 jest równy
jest równy
A) 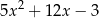 B)
B) 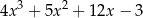
C) 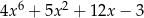 D)
D) 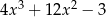
Wielomian 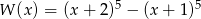 zapisano w postaci
zapisano w postaci 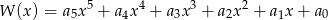 . Suma
. Suma 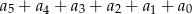 jest równa
jest równa
A) 275 B) 0 C) 1 D) 211
Wielomian 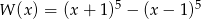 zapisano w postaci
zapisano w postaci 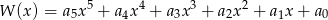 . Suma
. Suma 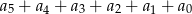 jest równa
jest równa
A) 32 B) 0 C) 1 D) 2
Wielomian 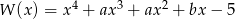 jest podzielny przez wielomian
jest podzielny przez wielomian 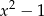 . Wynika stąd, że
. Wynika stąd, że
A) 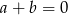 B)
B) 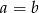 C)
C) 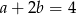 D)
D) 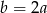
Pochodna funkcji 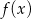 jest równa
jest równa 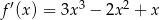 . Funkcja
. Funkcja 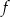 może mieć wzór
może mieć wzór
A) 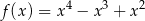 B)
B) 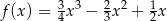
C) 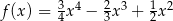 D)
D) 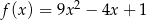
Wielomian 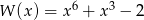 jest równy iloczynowi
jest równy iloczynowi
A) 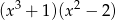 B)
B) 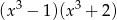 C)
C) 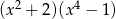 D)
D) 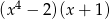
Wielomian 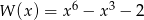 jest równy iloczynowi
jest równy iloczynowi
A) 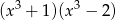 B)
B) 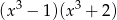 C)
C) 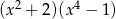 D)
D) 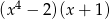
Wielomian 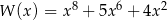 dla dowolnej liczby rzeczywistej
dla dowolnej liczby rzeczywistej  przyjmuje
przyjmuje
A) tylko wartości ujemne B) tylko wartości dodatnie
C) wartości niedodatnie D) wartości nieujemne
Wielomian 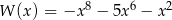 dla dowolnej liczby rzeczywistej
dla dowolnej liczby rzeczywistej  przyjmuje
przyjmuje
A) tylko wartości ujemne B) tylko wartości dodatnie
C) wartości niedodatnie D) wartości nieujemne
Wielomian 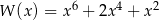 dla dowolnej liczby rzeczywistej
dla dowolnej liczby rzeczywistej  przyjmuje
przyjmuje
A) wartości niedodatnie B) wartości nieujemne
C) tylko wartości ujemne D) tylko wartości dodatnie

