Aby otrzymać wielomian 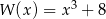 , należy pomnożyć wielomian
, należy pomnożyć wielomian 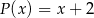 przez wielomian:
przez wielomian:
A) 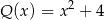 B)
B) 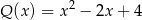
C) 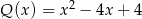 D)
D) 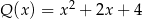
/Szkoła średnia/Zadania testowe/Funkcje/Wielomiany
Funkcja 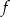 określona jest wzorem
określona jest wzorem 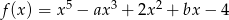 . Jeżeli
. Jeżeli 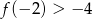 , to
, to
A) 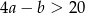 B)
B) 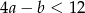 C)
C) 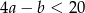 D)
D) 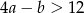
Który z wielomianów należy dodać do wielomianu 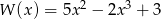 aby otrzymać wielomian
aby otrzymać wielomian 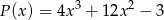 ?
?
A) 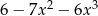 B)
B) 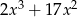 C)
C) 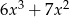 D)
D) 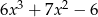
Wielomian 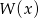 jest sumą wielomianów
jest sumą wielomianów 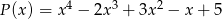 i
i 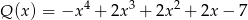 . Zatem stopień wielomianu
. Zatem stopień wielomianu 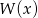 jest równy
jest równy
A) 16 B) 8 C) 4 D) 2
Dane są wielomiany 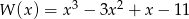 i
i 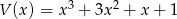 . Stopień wielomianu
. Stopień wielomianu 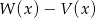 jest równy
jest równy
A) 0 B) 1 C) 2 D) 3
Dane są wielomiany 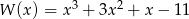 i
i 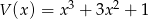 . Stopień wielomianu
. Stopień wielomianu 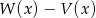 jest równy
jest równy
A) 0 B) 1 C) 2 D) 3
Wielomian 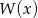 jest sumą wielomianów
jest sumą wielomianów 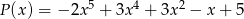 i
i 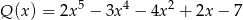 . Zatem stopień wielomianu
. Zatem stopień wielomianu 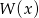 jest równy
jest równy
A) 2 B) 4 C) 5 D) 10
Reszta z dzielenia wielomianu 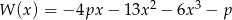 przez dwumian
przez dwumian 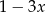 jest równa 3. Zatem
jest równa 3. Zatem
A) 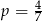 B)
B) 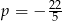 C)
C) 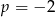 D)
D) 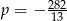
Pochodna funkcji 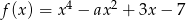 jest funkcją rosnącą jeżeli
jest funkcją rosnącą jeżeli
A) 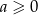 B)
B) 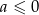 C)
C) 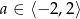 D)
D) 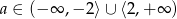
Wielomian 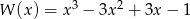
A) można przedstawić w postaci iloczynu trzech jednakowych czynników
B) dla argumentu 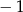 przyjmuje wartość
przyjmuje wartość 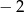
C) wartość równą 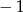 przyjmuje dla trzech argumentów
przyjmuje dla trzech argumentów
D) ma trzy różne pierwiastki
Wielomian 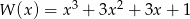
A) można przedstawić w postaci iloczynu trzech jednakowych czynników
B) dla argumentu 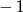 przyjmuje wartość
przyjmuje wartość 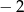
C) wartość równą 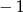 przyjmuje dla trzech argumentów
przyjmuje dla trzech argumentów
D) ma trzy różne pierwiastki
Wielomian 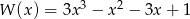
A) można przedstawić w postaci iloczynu trzech jednakowych czynników
B) dla argumentu 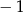 przyjmuje wartość
przyjmuje wartość 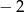
C) wartość równą 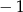 przyjmuje dla czterech argumentów
przyjmuje dla czterech argumentów
D) ma trzy różne pierwiastki
Stopień wielomianu 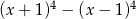 jest równy
jest równy
A) 4 B) 3 C) 2 D) 1
Styczna do wykresu funkcji 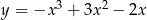 w punkcie
w punkcie 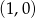 ma równanie
ma równanie
A) 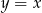 B)
B) 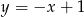 C)
C) 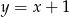 D)
D) 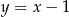
Styczna do wykresu funkcji 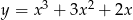 w punkcie
w punkcie 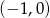 ma równanie
ma równanie
A) 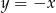 B)
B) 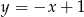 C)
C) 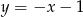 D)
D) 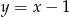
Funkcja określona dla każdej liczby rzeczywistej  wzorem
wzorem 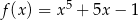
A) ma więcej niż dwa minima lokalne. B) ma dokładnie dwa minima lokalne.
C) ma dokładnie jedno minimum lokalne. D) nie ma minimum lokalnego.
Funkcja określona dla każdej liczby rzeczywistej  wzorem
wzorem 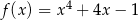
A) ma więcej niż dwa minima lokalne. B) ma dokładnie dwa minima lokalne.
C) ma dokładnie jedno minimum lokalne. D) nie ma minimum lokalnego.
Wiadomo, że 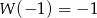 , gdy
, gdy 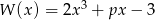 . Zatem wartość współczynnika
. Zatem wartość współczynnika 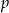 wynosi:
wynosi:
A) 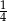 B) -4 C) 4 D) -1
B) -4 C) 4 D) -1
Dany jest wielomian 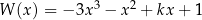 , gdzie
, gdzie 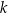 jest pewną liczbą rzeczywistą. Wiadomo, że wielomian
jest pewną liczbą rzeczywistą. Wiadomo, że wielomian 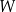 można zapisać w postaci
można zapisać w postaci 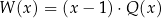 dla pewnego wielomianu
dla pewnego wielomianu 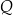 . Liczba
. Liczba 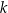 jest równa
jest równa
A) 29 B) 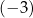 C) 0 D) 3
C) 0 D) 3
Dany jest wielomian 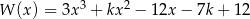 gdzie
gdzie 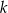 jest pewną liczbą rzeczywistą. Wiadomo, że liczba
jest pewną liczbą rzeczywistą. Wiadomo, że liczba 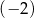 jest pierwiastkiem tego wielomianu. Liczba
jest pierwiastkiem tego wielomianu. Liczba 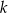 jest równa
jest równa
A) 2 B) 4 C) 6 D) 8
Dany jest wielomian 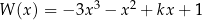 , gdzie
, gdzie 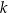 jest pewną liczbą rzeczywistą. Wiadomo, że wielomian
jest pewną liczbą rzeczywistą. Wiadomo, że wielomian 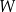 można zapisać w postaci
można zapisać w postaci 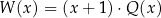 dla pewnego wielomianu
dla pewnego wielomianu 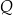 . Liczba
. Liczba 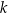 jest równa
jest równa
A) 29 B) 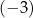 C) 0 D) 3
C) 0 D) 3
Dany jest wielomian 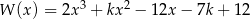 gdzie
gdzie 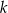 jest pewną liczbą rzeczywistą. Wiadomo, że liczba
jest pewną liczbą rzeczywistą. Wiadomo, że liczba 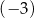 jest pierwiastkiem tego wielomianu. Liczba
jest pierwiastkiem tego wielomianu. Liczba 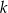 jest równa
jest równa
A) 2 B) 3 C) 6 D) 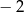
Wiadomo, że 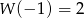 , gdy
, gdy 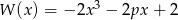 . Zatem wartość współczynnika
. Zatem wartość współczynnika 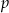 wynosi:
wynosi:
A) 6 B) -3 C) 3 D) -1
Przez jaki wielomian należy pomnożyć 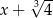 aby otrzymać wielomian
aby otrzymać wielomian 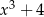 ?
?
A) 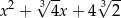 B)
B) 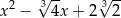
C) 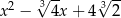 D)
D) 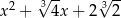
Wielomiany 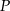 i
i 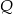 określone są wzorami
określone są wzorami 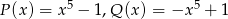 . Wielomian
. Wielomian 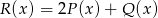 jest stopnia
jest stopnia
A) 0 B) 10 C) 1 D) 5
Wielomiany 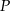 i
i 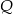 określone są wzorami
określone są wzorami 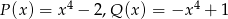 . Wielomian
. Wielomian 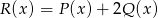 jest stopnia
jest stopnia
A) 0 B) 4 C) 2 D) 8
Wielomiany 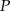 i
i 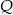 określone są wzorami
określone są wzorami 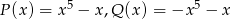 . Wielomian
. Wielomian 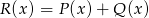 jest stopnia
jest stopnia
A) 0 B) 10 C) 1 D) 5
Dany jest wielomian 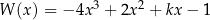 , gdzie
, gdzie 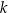 jest pewną liczbą rzeczywistą. Wiadomo, że wielomian
jest pewną liczbą rzeczywistą. Wiadomo, że wielomian 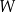 można zapisać w postaci
można zapisać w postaci 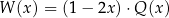 dla pewnego wielomianu
dla pewnego wielomianu 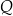 . Liczba
. Liczba 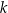 jest równa
jest równa
A) 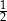 B) 2 C)
B) 2 C) 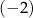 D)
D) 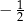
Wielomian 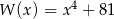 jest podzielny przez
jest podzielny przez
A) 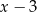 B)
B) 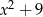 C)
C)  D)
D) 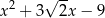
Wielomian 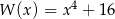 jest podzielny przez
jest podzielny przez
A) 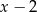 B)
B) 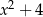 C)
C) 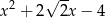 D)
D) 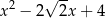
Funkcje 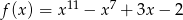 i
i 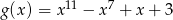 dla argumentu
dla argumentu  przyjmują tę samą wartość. Zatem
przyjmują tę samą wartość. Zatem
A) 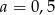 B)
B) 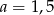 C)
C) 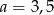 D)
D) 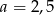
Funkcje 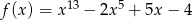 i
i 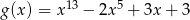 dla argumentu
dla argumentu  przyjmują tę samą wartość. Zatem
przyjmują tę samą wartość. Zatem
A) 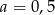 B)
B) 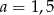 C)
C) 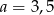 D)
D) 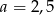
Dany jest wielomian 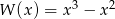 . Wartość tego wielomianu w punkcie
. Wartość tego wielomianu w punkcie 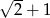 jest równa
jest równa
A) 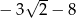 B)
B) 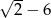 C)
C) 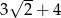 D)
D) 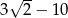
Dany jest wielomian 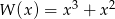 . Wartość tego wielomianu w punkcie
. Wartość tego wielomianu w punkcie 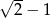 jest równa
jest równa
A) 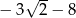 B)
B) 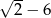 C)
C) 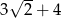 D)
D) 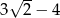
Dany jest wielomian 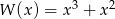 . Wartość tego wielomianu w punkcie
. Wartość tego wielomianu w punkcie 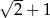 jest równa
jest równa
A) 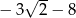 B)
B) 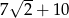 C)
C) 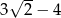 D)
D) 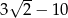
Wielomiany 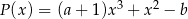 i
i 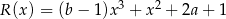 są równe. Zatem liczba
są równe. Zatem liczba 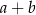
A) należy do zbioru 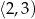 B) jest większa od 3
B) jest większa od 3
C) należy do zbioru 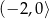 D) jest mniejsza od -2
D) jest mniejsza od -2
Iloczyn dwóch wielomianów, z których każdy jest stopnia piątego, może być wielomianem stopnia
A) drugiego B) szóstego C) dziesiątego D) dwudziestego piątego
Reszta z dzielenia wielomianu 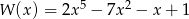 przez dwumian
przez dwumian 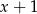 jest równa
jest równa
A) 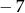 B) 7 C) 5 D) 11
B) 7 C) 5 D) 11
Reszta z dzielenia wielomianu 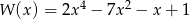 przez dwumian
przez dwumian 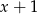 jest równa
jest równa
A) 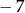 B) 7 C)
B) 7 C) 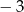 D) 11
D) 11
Reszta z dzielenia wielomianu 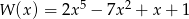 przez dwumian
przez dwumian 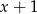 jest równa
jest równa
A) 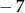 B)
B) 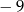 C) 5 D) 11
C) 5 D) 11
Reszta z dzielenia wielomianu 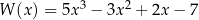 przez dwumian
przez dwumian 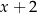 jest równa
jest równa
A) 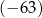 B)
B) 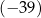 C) 25 D) 41
C) 25 D) 41
Reszta z dzielenia wielomianu 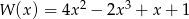 przez dwumian
przez dwumian 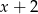 jest równa
jest równa
A) 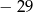 B) 3 C)
B) 3 C) 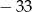 D) 31
D) 31
Reszta z dzielenia wielomianu 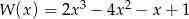 przez dwumian
przez dwumian 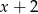 jest równa
jest równa
A) 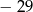 B) 3 C)
B) 3 C) 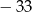 D)
D) 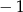
Reszta z dzielenia wielomianu 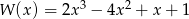 przez dwumian
przez dwumian 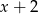 jest równa
jest równa
A) 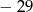 B) 3 C)
B) 3 C) 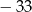 D)
D) 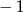
Reszta z dzielenia wielomianu 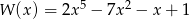 przez dwumian
przez dwumian 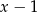 jest równa
jest równa
A) 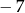 B) 7 C)
B) 7 C) 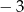 D)
D) 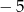
Reszta z dzielenia wielomianu 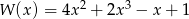 przez dwumian
przez dwumian 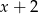 jest równa
jest równa
A) 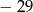 B) 3 C)
B) 3 C) 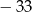 D) 35
D) 35
Reszta z dzielenia wielomianu 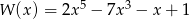 przez dwumian
przez dwumian 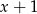 jest równa
jest równa
A) 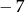 B) 7 C) 5 D) 11
B) 7 C) 5 D) 11

