Wielomian 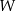 określony wzorem
określony wzorem 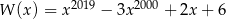
A) jest podzielny przez 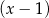 i z dzielenia przez
i z dzielenia przez 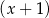 daje resztę równą 6.
daje resztę równą 6.
B) jest podzielny przez 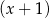 i z dzielenia przez
i z dzielenia przez 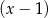 daje resztę równą 6.
daje resztę równą 6.
C) jest podzielny przez 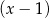 i jest podzielny przez
i jest podzielny przez 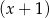 .
.
D) nie jest podzielny ani przez 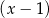 , ani przez
, ani przez 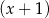 .
.
/Szkoła średnia/Zadania testowe/Funkcje/Wielomiany
Wielomian 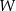 określony wzorem
określony wzorem 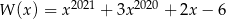
A) jest podzielny przez 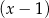 i z dzielenia przez
i z dzielenia przez 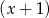 daje resztę równą
daje resztę równą 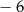 .
.
B) jest podzielny przez 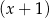 i z dzielenia przez
i z dzielenia przez 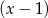 daje resztę równą
daje resztę równą 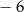 .
.
C) jest podzielny przez 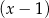 i jest podzielny przez
i jest podzielny przez 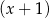 .
.
D) nie jest podzielny ani przez 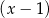 , ani przez
, ani przez 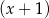 .
.
Reszta z dzielenia wielomianu 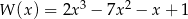 przez dwumian
przez dwumian 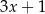 jest równa
jest równa
A) 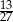 B)
B) 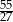 C)
C) 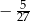 D)
D) 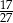
Reszta z dzielenia wielomianu 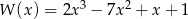 przez dwumian
przez dwumian 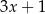 jest równa
jest równa
A) 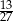 B)
B) 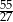 C)
C) 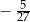 D)
D) 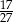
Wielomian 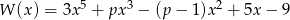 jest podzielny przez dwumian
jest podzielny przez dwumian 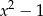 dla
dla 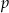 równego
równego
A) 6 B) 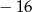 C) 4 D)
C) 4 D) 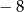
Dane są wielomiany 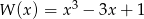 oraz
oraz 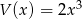 . Wielomian
. Wielomian 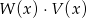 jest równy
jest równy
A) 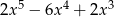 B)
B) 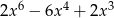 C)
C) 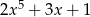 D)
D) 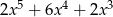
Dane są wielomiany 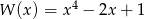 oraz
oraz 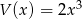 . Wielomian
. Wielomian 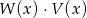 jest równy
jest równy
A) 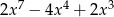 B)
B) 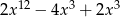 C)
C) 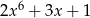 D)
D) 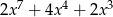
Dane są wielomiany 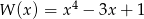 oraz
oraz 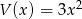 . Wielomian
. Wielomian 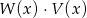 jest równy
jest równy
A) 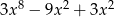 B)
B) 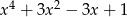 C)
C) 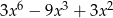 D)
D) 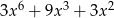
Dane są wielomiany 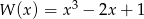 oraz
oraz 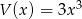 . Wielomian
. Wielomian 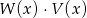 jest równy
jest równy
A) 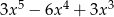 B)
B) 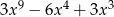 C)
C) 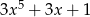 D)
D) 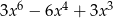
Iloczyn wielomianów 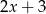 oraz
oraz 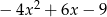 jest równy
jest równy
A) 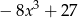 B)
B) 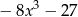 C)
C) 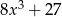 D)
D) 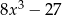
Iloczyn wielomianów 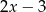 oraz
oraz 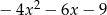 jest równy
jest równy
A) 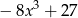 B)
B) 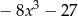 C)
C) 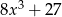 D)
D) 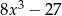
Wyraz wolny wielomianu 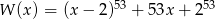 jest równy
jest równy
A) 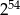 B) 0 C)
B) 0 C) 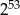 D) 53
D) 53
Wyraz wolny wielomianu 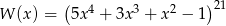 (po uporządkowaniu) jest równy
(po uporządkowaniu) jest równy
A) 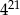 B)
B) 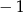 C) 1 D)
C) 1 D) 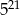
Wielomian 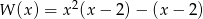 można zapisać w postaci
można zapisać w postaci
A) 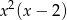 B)
B) 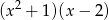 C)
C) 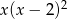 D)
D) 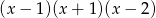
Wielomian 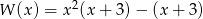 można zapisać w postaci
można zapisać w postaci
A) 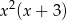 B)
B) 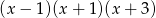 C)
C) 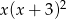 D)
D) 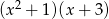
Wielomian 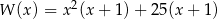 można przedstawić w postaci
można przedstawić w postaci
A) 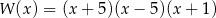 B)
B) 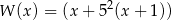
C) 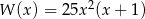 D)
D) 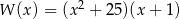
Wielomian 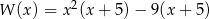 można przedstawić w postaci
można przedstawić w postaci
A) 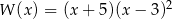 B)
B) 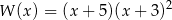
C) 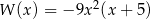 D)
D) 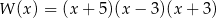
Wiadomo, że wśród pierwiastków wielomianu 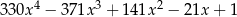 są odwrotności czterech różnych liczb pierwszych. Mediana wszystkich pierwiastków tego wielomianu jest równa
są odwrotności czterech różnych liczb pierwszych. Mediana wszystkich pierwiastków tego wielomianu jest równa
A) 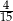 B)
B) 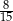 C)
C) 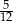 D)
D) 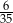
Wielomiany 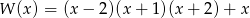 i
i 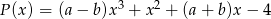 są równe. Z tego wynika, że
są równe. Z tego wynika, że
A) 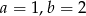 B)
B) 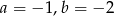 C)
C) 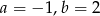 D)
D) 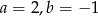
Wielomiany 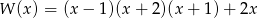 i
i 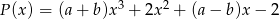 są równe. Z tego wynika, że
są równe. Z tego wynika, że
A) 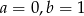 B)
B) 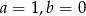 C)
C) 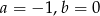 D)
D) 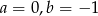
Wielomiany 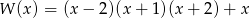 i
i 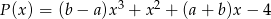 są równe. Z tego wynika, że
są równe. Z tego wynika, że
A) 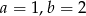 B)
B) 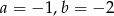 C)
C) 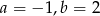 D)
D) 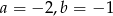
Stopień wielomianu 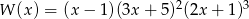 jest równy
jest równy
A) 4 B) 5 C) 6 D) 8
Stopień wielomianu 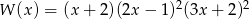 jest równy
jest równy
A) 4 B) 5 C) 6 D) 8
Stopień wielomianu 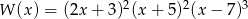 jest równy
jest równy
A) 4 B) 5 C) 6 D) 7
Wielomian 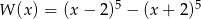 zapisano w postaci
zapisano w postaci 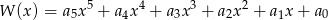 . Suma
. Suma 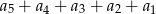 jest równa
jest równa
A) 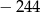 B)
B) 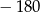 C)
C) 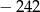 D)
D) 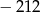
Wielomian 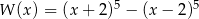 zapisano w postaci
zapisano w postaci 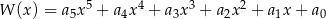 . Suma
. Suma 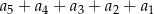 jest równa
jest równa
A) 180 B) 244 C) 242 D) 212
Wiadomo, że wielomian 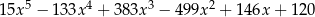 ma w zbiorze
ma w zbiorze 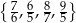 dokładnie jeden pierwiastek wymierny. Jest nim liczba
dokładnie jeden pierwiastek wymierny. Jest nim liczba
A) 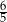 B)
B)  C)
C) 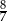 D)
D) 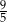
Wiadomo, że wielomian 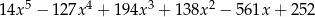 ma w zbiorze
ma w zbiorze 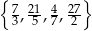 dokładnie jeden pierwiastek wymierny. Jest nim liczba
dokładnie jeden pierwiastek wymierny. Jest nim liczba
A)  B)
B) 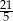 C)
C) 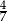 D)
D) 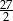
Suma współczynników wielomianu 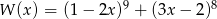 (po uporządkowaniu) jest równa
(po uporządkowaniu) jest równa
A) 0 B) 1 C) 2 D) 3
Suma współczynników wielomianu 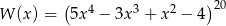 (po uporządkowaniu) jest równa
(po uporządkowaniu) jest równa
A) 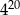 B)
B) 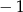 C) 1 D)
C) 1 D) 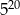
Suma wszystkich współczynników wielomianu 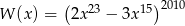 (po uporządkowaniu) wynosi
(po uporządkowaniu) wynosi
A) 0 B) 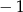 C) 1 D)
C) 1 D) 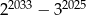
Suma wszystkich współczynników wielomianu 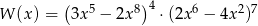 jest równa
jest równa
A) 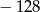 B) 216 C) 64 D)
B) 216 C) 64 D) 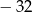
Suma współczynników wielomianu 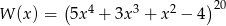 (po uporządkowaniu) jest równa
(po uporządkowaniu) jest równa
A) 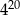 B)
B) 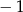 C) 1 D)
C) 1 D) 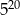
Suma wszystkich współczynników wielomianu 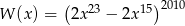 (po uporządkowaniu) wynosi
(po uporządkowaniu) wynosi
A) 0 B) 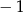 C) 1 D)
C) 1 D) 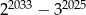
Suma wszystkich współczynników wielomianu 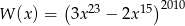 (po uporządkowaniu) wynosi
(po uporządkowaniu) wynosi
A) 0 B) 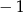 C) 1 D)
C) 1 D) 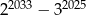
Wielomian 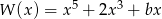 jest podzielny przez wielomian
jest podzielny przez wielomian 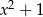 . Wynika stąd, że
. Wynika stąd, że
A) 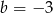 B)
B) 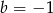 C)
C) 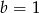 D)
D) 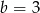
Wielomian 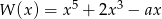 jest podzielny przez wielomian
jest podzielny przez wielomian 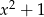 . Wynika stąd, że
. Wynika stąd, że
A) 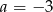 B)
B) 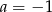 C)
C) 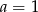 D)
D) 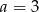
Wielomiany 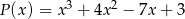 i
i 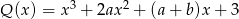 są równe. Zatem
są równe. Zatem
A) 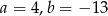 B)
B) 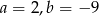 C)
C) 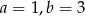 D)
D) 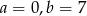
Wielomiany 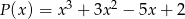 i
i 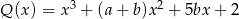 są równe. Zatem
są równe. Zatem
A) 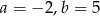 B)
B) 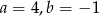 C)
C) 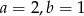 D)
D) 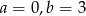
Która z poniższych funkcji jest rosnąca w zbiorze 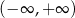 ?
?
A) 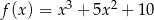 B)
B) 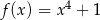
C) 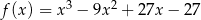 D)
D) 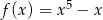
Wielomian 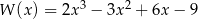 jest podzielny przez wielomian
jest podzielny przez wielomian
A) 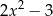 B)
B) 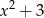 C)
C) 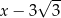 D)
D) 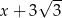
Wielomian 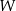 określony jest wzorem
określony jest wzorem 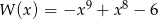 . Zatem
. Zatem 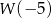 jest liczbą
jest liczbą
A) ujemną B) dodatnią C) niewymierną D) pierwszą
Wielomian 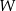 określony jest wzorem
określony jest wzorem 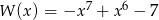 . Zatem
. Zatem 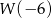 jest liczbą
jest liczbą
A) ujemną B) niewymierną C) dodatnią D) pierwszą
Wielomian 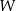 określony jest wzorem
określony jest wzorem 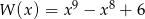 . Zatem
. Zatem 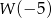 jest liczbą
jest liczbą
A) ujemną B) dodatnią C) niewymierną D) pierwszą
Po rozłożeniu wielomianu 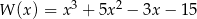 otrzymujemy
otrzymujemy
A) 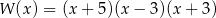 B)
B) 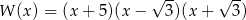
C) 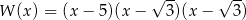 D)
D) 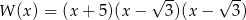
Wielomian 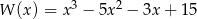 rozłożony na czynniki ma postać
rozłożony na czynniki ma postać
A) 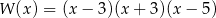 B)
B) 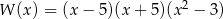
C) 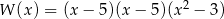 D)
D) 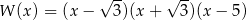
Wielomian 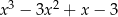 po rozłożeniu na czynniki ma postać:
po rozłożeniu na czynniki ma postać:
A) 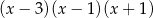 B)
B) 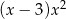
C) 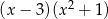 D)
D) 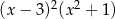
Wielomian 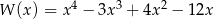 po rozłożeniu na czynniki ma postać:
po rozłożeniu na czynniki ma postać:
A) 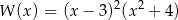 B)
B) 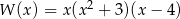
C) 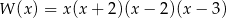 D)
D) 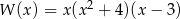
Wielomian 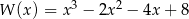 można przedstawić w postaci
można przedstawić w postaci
A) 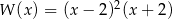 B)
B) 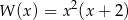
C) 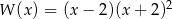 D)
D) 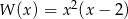
Reszta z dzielenia wielomianu 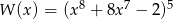 przez dwumian
przez dwumian 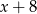 jest równa
jest równa
A) 32 B) 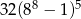 C)
C) 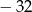 D)
D) 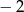
Reszta z dzielenia wielomianu 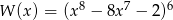 przez dwumian
przez dwumian 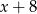 jest równa
jest równa
A) 64 B) 2 C) 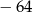 D)
D) 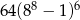
Reszta z dzielenia wielomianu 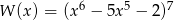 przez dwumian
przez dwumian 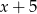 jest równa
jest równa
A) 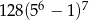 B)
B) 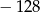 C)
C) 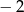 D) 128
D) 128
Reszta z dzielenia wielomianu 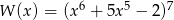 przez dwumian
przez dwumian 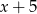 jest równa
jest równa
A) 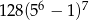 B)
B) 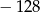 C)
C) 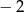 D) 128
D) 128
Reszta z dzielenia wielomianu 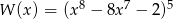 przez dwumian
przez dwumian 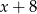 jest równa
jest równa
A) 32 B) 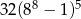 C)
C) 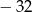 D)
D) 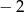
Reszta z dzielenia wielomianu 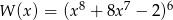 przez dwumian
przez dwumian 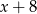 jest równa
jest równa
A) 64 B) 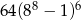 C)
C) 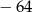 D)
D) 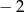
Reszta z dzielenia wielomianu 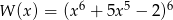 przez dwumian
przez dwumian 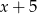 jest równa
jest równa
A) 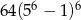 B)
B) 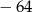 C)
C) 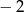 D) 64
D) 64
Iloczyn wielomianów 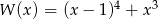 i
i 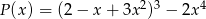 jest wielomianem stopnia
jest wielomianem stopnia
A) 24 B) 10 C) 12 D) 7

