Wartość wyrażenia 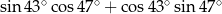 jest równa
jest równa
A) 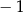 B) 0 C) 1 D) 2
B) 0 C) 1 D) 2
/Szkoła średnia/Zadania testowe/Funkcje/Trygonometryczna
Wartość wyrażenia 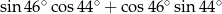 jest równa
jest równa
A) 1 B) 0 C) 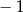 D) 2
D) 2
Liczba 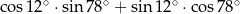 jest równa
jest równa
A) 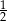 B)
B) 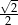 C)
C) 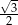 D) 1
D) 1
Wartość wyrażenia 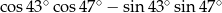 jest równa
jest równa
A) 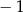 B) 0 C) 1 D) 2
B) 0 C) 1 D) 2
Wartość wyrażenia 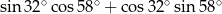 jest równa
jest równa
A) 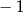 B) 1 C) 0 D) 2
B) 1 C) 0 D) 2
Wartość wyrażenia 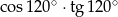 wynosi
wynosi
A) 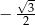 B) 1 C)
B) 1 C) 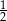 D)
D) 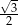
Wartość wyrażenia 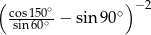 jest równa
jest równa
A) 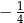 B)
B) 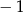 C) 1 D)
C) 1 D) 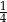
Wartość wyrażenia 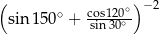 jest równa
jest równa
A) 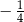 B) 4 C) 1 D)
B) 4 C) 1 D) 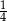
Dla każdego kąta  wyrażenie
wyrażenie 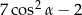 jest równe
jest równe
A) 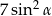 B)
B) 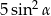
C)  D)
D) 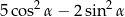
Liczba 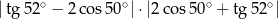 jest równa
jest równa
A) 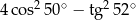 B)
B) 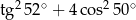
C) 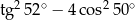 D)
D) 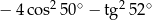
Wiadomo, że  jest kątem ostrym i
jest kątem ostrym i 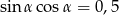 . Wynika stąd, że wartość wyrażenia
. Wynika stąd, że wartość wyrażenia 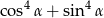 jest równa
jest równa
A) 1 B) 0,5 C) 0,25 D) 0,75
Wiadomo, że  jest kątem ostrym i
jest kątem ostrym i 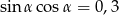 . Wynika stąd, że wartość wyrażenia
. Wynika stąd, że wartość wyrażenia 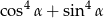 jest równa
jest równa
A) 0,18 B) 0,91 C) 0,82 D) 0,75
Wiadomo, że  jest kątem ostrym i
jest kątem ostrym i 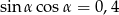 . Wynika stąd, że wartość wyrażenia
. Wynika stąd, że wartość wyrażenia 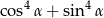 jest równa
jest równa
A) 0,68 B) 0,84 C) 0,32 D) 0,16
Jeżeli 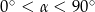 oraz
oraz 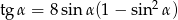 , to
, to
A) 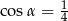 B)
B) 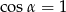 C)
C) 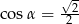 D)
D) 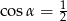
Jeżeli 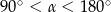 oraz
oraz 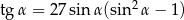 , to
, to
A) 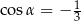 B)
B) 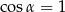 C)
C) 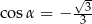 D)
D) 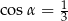
Kąt  jest kątem ostrym takim, że
jest kątem ostrym takim, że 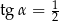 . Zatem
. Zatem
A) 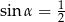 i
i 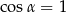 B)
B) 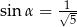 i
i 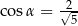
C) 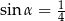 i
i 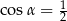 D)
D) 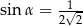 i
i 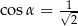
Kąt  jest kątem ostrym takim, że
jest kątem ostrym takim, że 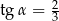 . Zatem
. Zatem
A) 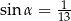 i
i 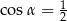 B)
B) 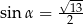 i
i 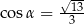
C) 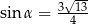 i
i 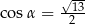 D)
D) 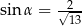 i
i 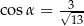
Ile wynosi 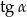 jeśli
jeśli 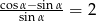 ?
?
A) 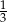 B) 3 C)
B) 3 C) 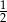 D) 2
D) 2
Okresem podstawowym funkcji 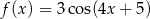 określonej dla
określonej dla 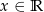 jest liczba
jest liczba
A) 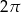 B)
B) 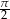 C)
C) 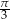 D)
D) 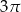
Wyrażenie 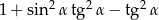 może być przekształcone do postaci
może być przekształcone do postaci
A) 1 B) 0 C) 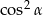 D)
D) 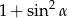
Dla każdego kąta ostrego  wyrażenie
wyrażenie 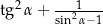 jest równe
jest równe
A) 1 B)  C)
C) 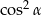 D)
D) 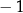
Kąt  jest kątem ostrym i
jest kątem ostrym i 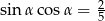 . Wówczas wyrażenie
. Wówczas wyrażenie 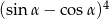 jest równe
jest równe
A) 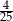 B)
B) 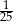 C)
C) 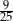 D)
D) 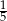
Wiadomo, że 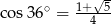 . Zatem
. Zatem
A) 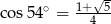 B)
B) 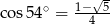 C)
C) 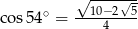 D)
D) 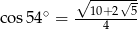
Jeżeli 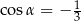 i
i  jest kątem rozwartym, to wartość
jest kątem rozwartym, to wartość 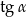 jest równa
jest równa
A) 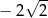 B)
B) 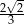 C)
C) 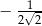 D)
D) 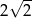
Wyrażenie 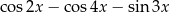 jest równe
jest równe
A) 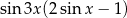 B)
B) 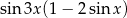
C) 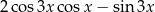 D)
D) 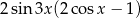
Wartość wyrażenia 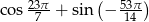 jest równa
jest równa
A) 0 B) 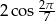 C)
C) 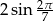 D)
D) 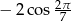
Kąt  jest ostry i
jest ostry i 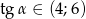 . Wtedy liczba
. Wtedy liczba 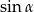 należy do przedziału
należy do przedziału
A) 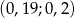 B)
B) 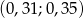 C)
C) 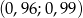 D)
D) 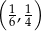
Kąt  jest ostry i
jest ostry i 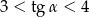 . Wtedy liczba
. Wtedy liczba 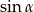 należy do przedziału
należy do przedziału
A) 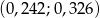 B)
B) 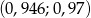 C)
C) 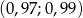 D)
D) 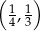
Wyrażenie 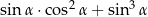 , gdzie
, gdzie  jest kątem ostrym, jest równe
jest kątem ostrym, jest równe
A) 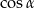 B) 1 C)
B) 1 C)  D)
D) 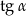
Wyrażenie 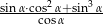 , gdzie
, gdzie  jest kątem ostrym, jest równe
jest kątem ostrym, jest równe
A) 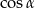 B) 1 C)
B) 1 C) 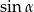 D)
D) 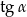
Dla każdego kąta ostrego  wyrażenie
wyrażenie 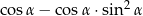 jest równe
jest równe
A) 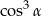 B)
B) 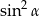 C)
C)  D)
D) 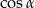
Dla każdego kąta ostrego  wyrażenie
wyrażenie 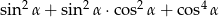 jest równe
jest równe
A) 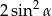 B)
B) 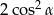 C) 1 D) 2
C) 1 D) 2
Dla każdego kąta ostrego  wyrażenie
wyrażenie 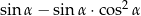 jest równe
jest równe
A) 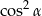 B)
B) 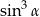 C)
C) 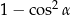 D)
D) 
Dla każdego kąta ostrego  wyrażenie
wyrażenie 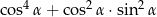 jest równe
jest równe
A) 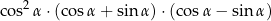 B)
B) 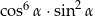
C) 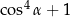 D)
D) 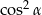
Dla każdego kąta ostrego  wyrażenie
wyrażenie 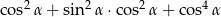 jest równe
jest równe
A) 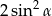 B)
B) 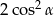 C) 1 D) 2
C) 1 D) 2
Dla każdego kąta ostrego  wyrażenie
wyrażenie 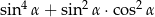 jest równe
jest równe
A) 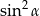 B)
B) 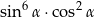
C) 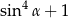 D)
D) 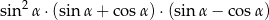
Wyrażenie 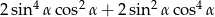 może być przekształcone do postaci
może być przekształcone do postaci
A) 2 B) 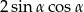 C)
C) 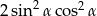 D)
D) 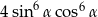
Wyrażenie 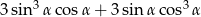 może być przekształcone do postaci
może być przekształcone do postaci
A) 3 B) 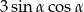 C)
C) 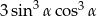 D)
D) 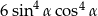
Wyrażenie 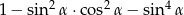 , gdzie
, gdzie  jest kątem ostrym, jest równe
jest kątem ostrym, jest równe
A) 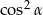 B) 1 C)
B) 1 C) 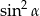 D)
D) 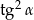
Wartość wyrażenia 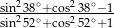 jest równa
jest równa
A) 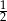 B) 0 C)
B) 0 C) 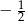 D) 1
D) 1
Wartość wyrażenia 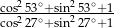 jest równa
jest równa
A) 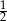 B) 0 C)
B) 0 C) 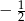 D) 1
D) 1
Nieprawdą jest, że
A) 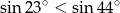 B)
B) 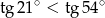 C)
C) 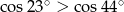 D)
D) 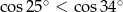
Nieprawdą jest, że
A) 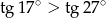 B)
B) 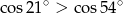 C)
C) 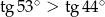 D)
D) 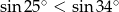
Nieprawdą jest, że
A) 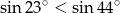 B)
B) 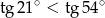 C)
C) 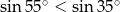 D)
D) 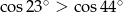
Nieprawdą jest, że
A) 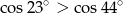 B)
B) 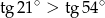 C)
C) 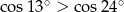 D)
D) 

