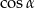Liczba 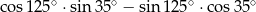 jest równa
jest równa
A) 1 B) 0 C) 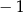 D)
D) 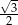
/Szkoła średnia/Zadania testowe/Funkcje/Trygonometryczna
Wartość wyrażenia 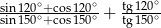 jest równa
jest równa
A) 4 B) 0 C) 1 D) 2
Kąt  jest ostry i
jest ostry i 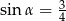 . Wartość wyrażenia
. Wartość wyrażenia 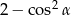 jest równa
jest równa
A) 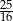 B)
B)  C)
C) 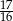 D)
D) 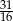
Kąt  jest ostry i
jest ostry i 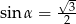 . Wartość wyrażenia
. Wartość wyrażenia 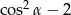 jest równa
jest równa
A) 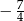 B)
B) 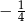 C)
C) 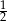 D)
D) 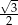
Kąt  jest ostry i
jest ostry i 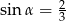 . Wartość wyrażenia
. Wartość wyrażenia 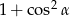 jest równa
jest równa
A) 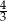 B)
B) 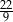 C)
C) 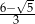 D)
D) 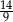
Kąt  jest ostry i
jest ostry i 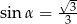 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 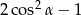 jest równa
jest równa
A) 0 B) 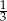 C)
C) 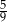 D) 1
D) 1
Kąt  jest ostry i
jest ostry i 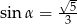 . Wartość wyrażenia
. Wartość wyrażenia 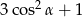 jest równa
jest równa
A)  B)
B) 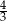 C)
C)  D)
D) 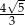
Wartość wyrażenia 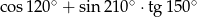 jest równa
jest równa
A) 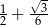 B)
B) 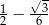 C)
C) 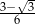 D)
D) 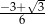
Wartość wyrażenia 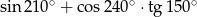 jest równa
jest równa
A) 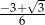 B)
B) 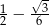 C)
C) 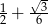 D)
D) 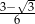
Wyrażenie 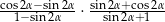 , gdzie
, gdzie  jest kątem ostrym, jest równe
jest kątem ostrym, jest równe
A) 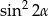 B)
B) 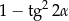 C)
C) 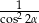 D)
D) 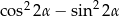
Kąt  jest ostry i
jest ostry i 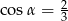 . Wartość wyrażenia
. Wartość wyrażenia 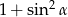 jest równa
jest równa
A) 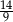 B)
B) 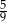 C)
C)  D)
D) 
Kąt  jest ostry i
jest ostry i 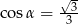 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 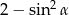 jest równa
jest równa
A) 0 B)  C)
C) 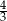 D) 1
D) 1
Kąt  jest kątem ostrym i
jest kątem ostrym i 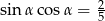 . Wówczas wyrażenie
. Wówczas wyrażenie 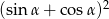 jest równe
jest równe
A)  B)
B)  C)
C) 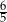 D) 1
D) 1
Kąt  jest kątem ostrym i
jest kątem ostrym i 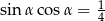 . Wówczas wyrażenie
. Wówczas wyrażenie 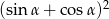 jest równe
jest równe
A)  B)
B) 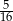 C)
C)  D) 1
D) 1
Kąt  jest kątem ostrym i
jest kątem ostrym i 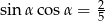 . Wówczas wyrażenie
. Wówczas wyrażenie 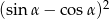 jest równe
jest równe
A) 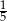 B)
B)  C)
C)  D) 1
D) 1
Liczba 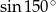 jest równa liczbie
jest równa liczbie
A) 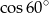 B)
B) 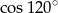 C)
C) 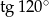 D)
D) 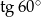
Liczba 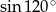 jest równa liczbie
jest równa liczbie
A) 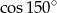 B)
B) 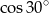 C)
C) 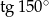 D)
D) 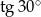
Liczba 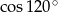 jest równa liczbie
jest równa liczbie
A) 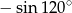 B)
B) 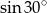 C)
C) 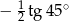 D)
D) 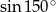
W trójkącie prostokątnym dane są kąty ostre: 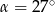 i
i 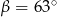 . Wtedy
. Wtedy 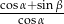 równa się
równa się
A) 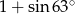 B)
B) 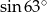 C) 1 D) 2
C) 1 D) 2
W trójkącie prostokątnym dane są kąty ostre: 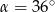 i
i 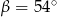 . Wtedy
. Wtedy 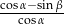 równa się
równa się
A) 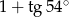 B)
B) 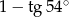 C) 1 D) 0
C) 1 D) 0
Kąt  jest ostry i
jest ostry i 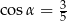 . Wtedy
. Wtedy
A) 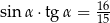 B)
B) 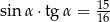 C)
C) 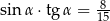 D)
D) 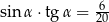
Kąt  jest ostry i
jest ostry i 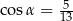 . Wtedy
. Wtedy
A) 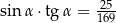 B)
B) 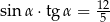 C)
C) 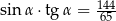 D)
D) 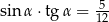
Kąt  jest ostry i
jest ostry i 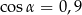 . Wówczas
. Wówczas
A) 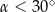 B)
B) 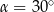 C)
C) 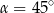 D)
D) 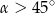
Kąt  jest kątem ostrym i
jest kątem ostrym i 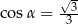 . Zatem
. Zatem
A) 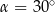 B)
B) 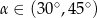 C)
C) 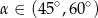 D)
D) 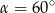
Kąt  jest ostry i
jest ostry i 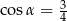 . Wówczas
. Wówczas
A) 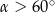 B)
B) 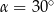 C)
C) 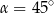 D)
D) 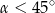
Kąt  jest ostry oraz
jest ostry oraz 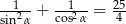 . Wartość wyrażenia
. Wartość wyrażenia 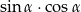 jest równa
jest równa
A)  B)
B)  C)
C) 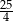 D)
D) 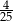
Kąt  jest rozwarty oraz
jest rozwarty oraz 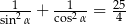 . Wartość wyrażenia
. Wartość wyrażenia 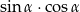 jest równa
jest równa
A) 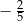 B)
B)  C)
C) 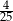 D)
D) 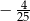
Dla kąta ostrego  spełniony jest warunek
spełniony jest warunek 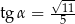 . Wówczas
. Wówczas
A) 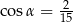 B)
B) 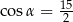 C)
C) 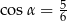 D)
D) 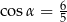
Kąt  jest ostry i
jest ostry i 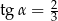 . Wtedy
. Wtedy
A) 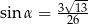 B)
B) 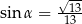 C)
C) 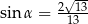 D)
D) 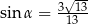
Kąt  jest ostry i
jest ostry i 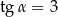 . Wobec tego
. Wobec tego
A) 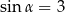 i
i 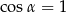 B)
B) 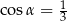 C)
C) 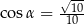 D)
D) 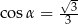
Kąt  jest ostry i
jest ostry i 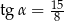 . Wówczas
. Wówczas 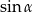 jest równy
jest równy
A) 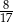 B)
B) 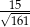 C)
C) 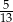 D)
D) 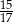
Dla kąta ostrego  spełniony jest warunek
spełniony jest warunek 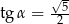 . Wówczas
. Wówczas
A) 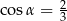 B)
B) 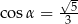 C)
C) 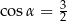 D)
D) 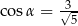
Dla kąta ostrego  spełniony jest warunek
spełniony jest warunek 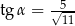 . Wówczas
. Wówczas
A) 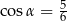 B)
B) 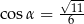 C)
C) 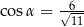 D)
D) 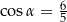
Kąt  jest ostry i
jest ostry i 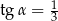 . Wtedy
. Wtedy
A) 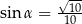 B)
B) 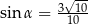 C)
C) 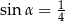 D)
D) 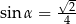
Kąt  jest ostry i
jest ostry i 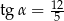 . Wówczas
. Wówczas 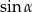 jest równy
jest równy
A) 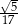 B)
B) 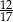 C)
C) 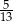 D)
D) 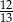
Kąt  jest ostry i
jest ostry i 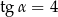 . Wobec tego
. Wobec tego
A) 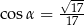 B)
B) 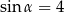 i
i 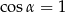 C)
C) 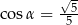 D)
D) 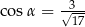
Kąt  jest kątem ostrym oraz
jest kątem ostrym oraz 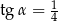 . Zatem
. Zatem
A) 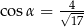 B)
B) 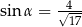 C)
C) 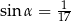 D)
D) 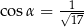
Kąt  jest kątem ostrym oraz
jest kątem ostrym oraz 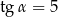 . Zatem
. Zatem
A) 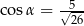 B)
B) 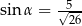 C)
C) 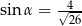 D)
D) 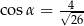
Kąt  jest ostry i
jest ostry i 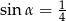 . Wówczas
. Wówczas
A) 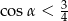 B)
B) 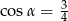 C)
C) 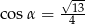 D)
D) 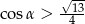
Kąt  jest ostry i
jest ostry i 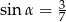 . Wówczas
. Wówczas
A) 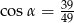 B)
B) 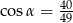 C)
C) 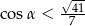 D)
D) 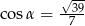
Liczba 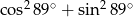 jest
jest
A) ujemna B) niewymierna C) parzysta D) nieparzysta
Liczba 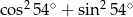 jest
jest
A) dodatnia B) niewymierna C) parzysta D) ujemna
Kąt  jest ostry i
jest ostry i 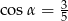 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 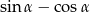 jest równa
jest równa
A) 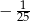 B)
B)  C)
C) 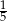 D)
D) 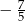
Jeśli 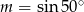 , to
, to
A) 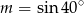 B)
B) 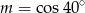 C)
C) 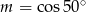 D)
D) 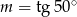
Jeśli 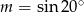 , to
, to
A) 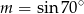 B)
B) 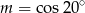 C)
C) 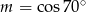 D)
D) 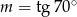
Wiadomo, że kąt  jest kątem ostrym i
jest kątem ostrym i 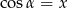 . Wtedy
. Wtedy 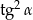 równa się
równa się
A) 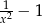 B)
B) 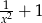 C)
C) 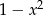 D)
D) 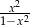
Wiadomo, że kąt  jest kątem ostrym i
jest kątem ostrym i 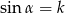 . Wtedy
. Wtedy 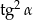 równa się
równa się
A) 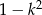 B)
B) 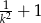 C)
C) 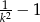 D)
D) 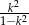
Wiadomo, że kąt  jest kątem ostrym i
jest kątem ostrym i 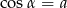 . Wtedy
. Wtedy 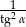 równa się
równa się
A) 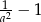 B)
B) 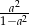 C)
C) 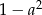 D)
D) 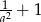
Kąt  jest ostry i
jest ostry i 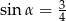 . Wówczas
. Wówczas
A) 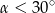 B)
B) 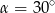 C)
C) 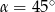 D)
D) 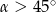
Jeśli  jest kątem ostrym i
jest kątem ostrym i 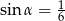 , to
, to
A) 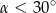 B)
B) 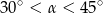 C)
C) 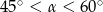 D)
D) 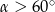
Kąt  jest ostry oraz
jest ostry oraz 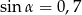 . Zatem
. Zatem
A) 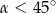 B)
B) 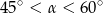 C)
C) 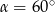 D)
D) 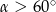
Kąt  jest ostry i
jest ostry i 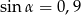 . Wówczas
. Wówczas
A) 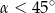 B)
B) 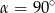 C)
C) 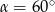 D)
D) 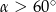
Wartość wyrażenia 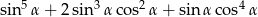 jest równa
jest równa
A) 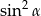 B)
B) 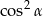 C)
C) 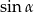 D)
D) 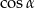
Wyrażenie 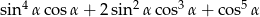 jest równe
jest równe
A) 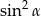 B)
B) 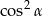 C)
C) 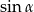 D)
D)