Przekrojem osiowym stożka jest trójkąt równoboczny o boku długości 6. Objętość tego stożka jest równa
A) 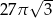 B)
B) 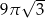 C)
C) 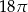 D)
D) 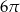
/Szkoła średnia/Zadania testowe/Geometria/Stereometria/Stożek
Przekrojem osiowym stożka jest trójkąt równoboczny o boku długości 4. Objętość tego stożka jest równa
A) 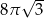 B)
B) 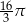 C)
C) 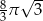 D)
D) 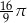
Trójkąt prostokątny o przyprostokątnych 4 i 6 obracamy wokół dłuższej przyprostokątnej. Objętość powstałego stożka jest równa:
A) 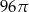 B)
B) 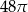 C)
C) 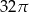 D)
D) 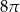
Dany jest stożek o wysokości 6 i tworzącej 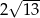 . Objętość tego stożka jest równa
. Objętość tego stożka jest równa
A) 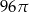 B)
B) 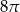 C)
C) 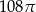 D)
D) 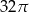
Trójkąt prostokątny o przyprostokątnych 4 i 6 obracamy wokół krótszej przyprostokątnej. Objętość powstałego stożka jest równa:
A) 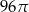 B)
B) 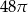 C)
C) 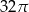 D)
D) 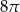
Dany jest stożek o wysokości 6 i tworzącej 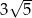 . Objętość tego stożka jest równa
. Objętość tego stożka jest równa
A) 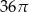 B)
B) 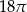 C)
C) 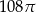 D)
D) 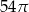
Pole powierzchni bocznej stożka wynosi 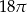 . Jeżeli przekrój osiowy stożka jest trójkątem równobocznym, to pole tego przekroju jest równe:
. Jeżeli przekrój osiowy stożka jest trójkątem równobocznym, to pole tego przekroju jest równe:
A) 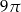 B)
B) 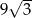 C)
C) 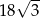 D)
D) 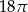
Pole powierzchni bocznej stożka wynosi 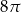 . Jeżeli przekrój osiowy stożka jest trójkątem równobocznym, to pole tego przekroju jest równe:
. Jeżeli przekrój osiowy stożka jest trójkątem równobocznym, to pole tego przekroju jest równe:
A) 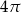 B)
B) 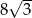 C)
C) 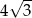 D)
D) 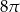
Przekrój osiowy stożka jest trójkątem równoramiennym o podstawie 8 i ramieniu 10. Powierzchnia boczna stożka jest wycinkiem koła o kącie środkowym
A) 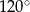 B)
B) 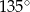 C)
C) 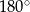 D)
D) 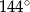
Trójkąt równoboczny o boku długości 4 cm obrócono wokół prostej zawierającej wysokość trójkąta. Objętość powstałej bryły jest równa:
A) 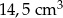 B)
B) 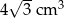 C)
C) 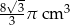 D)
D) 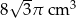
Trójkąt równoboczny o boku długości 6 cm obrócono wokół prostej zawierającej wysokość trójkąta. Objętość powstałej bryły jest równa:
A) 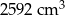 B)
B) 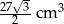 C)
C) 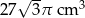 D)
D) 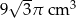
Pole powierzchni bocznej stożka o wysokości 4 i promieniu podstawy 3 jest równe
A) 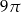 B)
B) 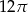 C)
C) 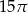 D)
D) 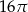
Pole powierzchni bocznej stożka o wysokości 12 i promieniu podstawy 5 jest równe
A) 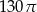 B)
B) 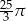 C)
C) 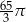 D)
D) 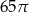
Stożek powstał w wyniku obrotu trójkąta prostokątnego o przyprostokątnych 13 i 15 wokół dłuższej przyprostokątnej. Promień podstawy tego stożka jest równy
A) 15 B) 13 C) 7,5 D) 6,5
Trójkąt prostokątny o przyprostokątnych długości 12 i 5 obrócono wokół krótszego boku. Pole powierzchni bocznej tak otrzymanej bryły jest równe
A) 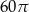 B)
B) 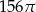 C)
C) 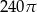 D)
D) 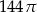
Trójkąt prostokątny o przyprostokątnych długości 8 i 6 obrócono wokół dłuższej przyprostokątnej. Pole powierzchni bocznej tak otrzymanej bryły jest równe
A) 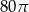 B)
B) 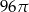 C)
C) 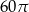 D)
D) 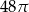
Trójkąt prostokątny o przyprostokątnych długości 12 i 5 obrócono wokół dłuższej przyprostokątnej. Pole powierzchni bocznej tak otrzymanej bryły jest równe
A) 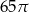 B)
B) 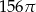 C)
C) 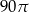 D)
D) 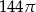
Długość tworzącej stożka jest równa średnicy jego podstawy. Pole powierzchni bocznej stożka jest równe 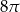 . Pole podstawy stożka jest równe
. Pole podstawy stożka jest równe
A) 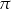 B)
B) 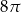 C)
C) 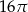 D)
D) 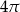
Długość tworzącej stożka jest 4 razy większa niż długość średnicy jego podstawy. Pole powierzchni bocznej stożka jest równe 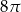 . Pole podstawy stożka jest równe
. Pole podstawy stożka jest równe
A) 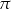 B)
B) 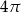 C)
C) 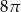 D)
D) 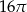
Długość tworzącej stożka jest dwa razy dłuższa niż średnica jego podstawy. Pole powierzchni bocznej stożka jest równe 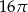 . Pole podstawy stożka jest równe
. Pole podstawy stożka jest równe
A) 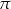 B)
B) 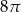 C)
C) 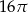 D)
D) 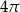
Półkole o promieniu 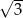 cm zwinięto w stożek.
cm zwinięto w stożek.
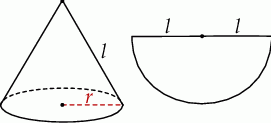
Wysokość tego stożka jest równa
A) 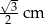 B)
B) 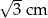 C) 3 cm D) 1,5 cm
C) 3 cm D) 1,5 cm
Jeżeli promień podstawy stożka zwiększymy o 20%, a wysokość zmniejszymy o 20%, to objętość stożka
A) nie zmieni się B) zwiększy się o 15,2%
C) zwiększy się o 1,52% D) zmniejszy się o 4%
Jeżeli promień podstawy stożka zwiększymy o 10%, a wysokość zmniejszymy o 10%, to objętość stożka
A) zwiększy się o 0,89% B) nie zmieni się
C) zmniejszy się o 0,89% D) zwiększy się o 8,9%
Jeżeli promień podstawy stożka zmniejszymy o 20%, a wysokość zwiększymy o 20%, to objętość stożka
A) nie zmieni się B) zwiększy się o 2,32%
C) zmniejszy się o 76,8% D) zmniejszy się o 23,2%
Stożki 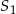 oraz
oraz 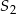 mają równe wysokości. Promień podstawy stożka
mają równe wysokości. Promień podstawy stożka 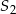 jest 4 razy dłuższy od promienia stożka
jest 4 razy dłuższy od promienia stożka 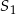 . Wobec tego objętość stożka
. Wobec tego objętość stożka 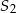 jest
jest
A) 4 razy większa od objętości stożka 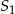
B) o 150% większa od objętości stożka 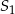
C) o 300% większa od objętości stożka 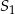
D) o 1500% większa od objętości stożka 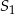
Stożki 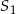 oraz
oraz 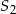 mają równe promienie podstawy. Wysokość stożka
mają równe promienie podstawy. Wysokość stożka 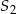 jest 4 razy dłuższa od wysokości stożka
jest 4 razy dłuższa od wysokości stożka 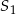 . Wobec tego objętość stożka
. Wobec tego objętość stożka 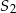 jest
jest
A) 4 razy większa od objętości stożka 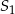
B) o 150% większa od objętości stożka 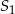
C) o 400% większa od objętości stożka 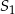
D) 0 1500% większa od objętości stożka 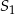
Stożki 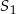 oraz
oraz 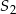 mają równe wysokości. Promień podstawy stożka
mają równe wysokości. Promień podstawy stożka 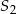 jest 2 razy dłuższy od promienia stożka
jest 2 razy dłuższy od promienia stożka 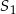 . Wobec tego objętość stożka
. Wobec tego objętość stożka 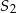 jest
jest
A) 4 razy większa od objętości stożka 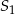
B) o 150% większa od objętości stożka 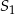
C) o 400% większa od objętości stożka 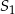
D) o 1500% większa od objętości stożka 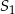
Pole powierzchni całkowitej pewnego stożka jest 3 razy większe od pola powierzchni pewnej kuli. Promień tej kuli jest równy 2 i jest taki sam jak promień podstawy tego stożka. Tworząca tego stożka ma długość równą
A) 12 B) 11 C) 24 D) 22
Pole powierzchni całkowitej pewnego stożka jest 4 razy większe od pola powierzchni pewnej kuli. Promień tej kuli jest równy 3 i jest taki sam jak promień podstawy tego stożka. Tworząca tego stożka ma długość równą
A) 42 B) 45 C) 48 D) 52
Hania zaprojektowała i wykonała czapeczkę na bal urodzinowy młodszego brata. Czapeczka miała kształt powierzchni bocznej stożka o średnicy podstawy 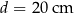 , wysokości
, wysokości 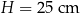 i tworzącej
i tworzącej 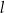 . Żeby wykonać czapeczkę, Hania najpierw narysowała na kartonie figurę płaską
. Żeby wykonać czapeczkę, Hania najpierw narysowała na kartonie figurę płaską 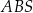 o kształcie wycinka koła o promieniu
o kształcie wycinka koła o promieniu 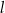 i środku
i środku 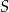 . Następnie wycięła tę figurę z kartonu, odpowiednio ją wymodelowała i skleiła odcinek
. Następnie wycięła tę figurę z kartonu, odpowiednio ją wymodelowała i skleiła odcinek 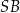 z odcinkiem
z odcinkiem 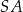 .
.

Kąt rozwarcia stożka, którego powierzchnią boczną jest czapeczka, ma miarę (w zaokrągleniu do 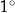 )
)
A) 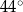 B)
B) 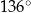 C)
C) 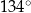 D)
D) 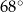
Trójkąt prostokątny 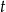 obrócono względem dłuższej przyprostokątnej i otrzymano stożek o polu powierzchni bocznej
obrócono względem dłuższej przyprostokątnej i otrzymano stożek o polu powierzchni bocznej 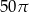 i kącie rozwarcia
i kącie rozwarcia 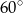 . Obwód trójkąta
. Obwód trójkąta 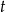 jest równy
jest równy
A) 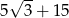 B)
B) 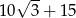 C)
C) 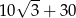 D)
D) 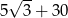
Przekrój osiowy stożka jest trójkątem o polu 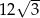 . Tworząca stożka jest nachylona do płaszczyzny podstawy pod kątem
. Tworząca stożka jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 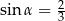 . Pole powierzchni bocznej tego stożka jest równe
. Pole powierzchni bocznej tego stożka jest równe
A) 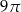 B)
B) 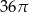 C)
C) 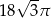 D)
D) 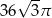
Tworząca stożka jest nachylona do płaszczyzny podstawy pod kątem 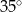 . Miara kąta rozwarcia stożka jest równa
. Miara kąta rozwarcia stożka jest równa
A) 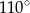 B)
B) 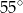 C)
C) 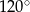 D)
D) 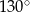
Pole powierzchni bocznej stożka o kącie rozwarcia 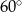 i wysokości
i wysokości 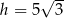 jest równe
jest równe
A) 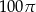 B)
B) 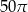 C)
C) 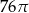 D)
D) 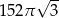
Pole powierzchni bocznej stożka o kącie rozwarcia 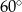 i wysokości
i wysokości 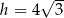 jest równe
jest równe
A) 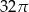 B)
B) 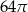 C)
C) 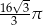 D)
D) 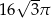
Pole powierzchni bocznej stożka o kącie rozwarcia 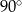 i wysokości
i wysokości 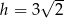 jest równe
jest równe
A) 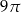 B)
B) 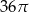 C)
C) 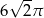 D)
D) 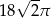
Pole powierzchni bocznej stożka o kącie rozwarcia 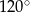 i wysokości
i wysokości 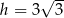 jest równe
jest równe
A) 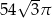 B)
B) 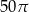 C)
C) 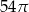 D)
D) 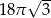
Dany jest stożek, którego przekrojem osiowym jest trójkąt o bokach długości: 6, 10 i 10. Stosunek pola powierzchni bocznej stożka do pola jego podstawy jest równy
A) 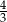 B)
B) 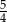 C)
C) 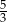 D)
D) 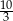
Pole powierzchni bocznej stożka jest dwa razy większe od jego pola podstawy. Tworząca tego stożka jest nachylona do płaszczyzny podstawy pod kątem
A) 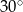 B)
B) 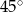 C)
C) 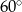 D)
D)