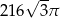Pole powierzchni całkowitej pewnego stożka jest 5 razy większe od pola powierzchni pewnej kuli. Promień tej kuli jest taki sam jak promień podstawy tego stożka. Tworząca tego stożka jest nachylona do podstawy pod kątem  takim, że
takim, że
A) 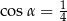 B)
B) 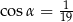 C)
C) 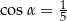 D)
D) 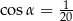
/Szkoła średnia/Zadania testowe/Geometria/Stereometria/Stożek
Przekrój osiowy stożka jest trójkątem równobocznym o boku długości 6.
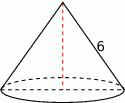
Pole powierzchni bocznej tego stożka jest równe
A) 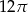 B)
B) 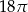 C)
C) 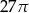 D)
D) 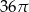
Przekrój osiowy stożka jest trójkątem równobocznym o boku długości 8.
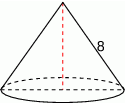
Pole powierzchni bocznej tego stożka jest równe
A) 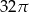 B)
B) 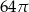 C)
C) 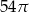 D)
D) 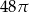
Pole powierzchni bocznej stożka o kącie rozwarcia 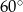 i promieniu podstawy 3 cm jest równe
i promieniu podstawy 3 cm jest równe
A) 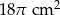 B)
B) 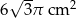 C)
C) 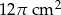 D)
D) 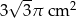
Przekrój osiowy stożka jest trójkątem równobocznym o boku długości 4.
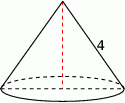
Pole powierzchni bocznej tego stożka jest równe
A) 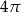 B)
B) 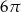 C)
C) 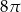 D)
D) 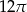
Szklane naczynie w kształcie stożka o promieniu podstawy 6 cm i wysokości 9 cm napełniono wodą do  wysokości (zobacz rysunek).
wysokości (zobacz rysunek).
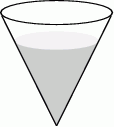
Objętość wody w naczyniu jest równa
A) 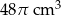 B)
B) 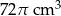 C)
C) 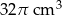 D)
D) 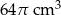
Szklane naczynie w kształcie stożka o promieniu podstawy 8 cm i wysokości 9 cm napełniono wodą do  wysokości (zobacz rysunek).
wysokości (zobacz rysunek).
Objętość wody w naczyniu jest równa
A) 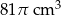 B)
B) 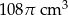 C)
C) 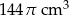 D)
D) 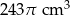
Stożek o promieniu podstawy  i kula o tym samym promieniu mają równe objętości. Tangens kąta między tworzącą i płaszczyzną podstawy tego stożka jest równy
i kula o tym samym promieniu mają równe objętości. Tangens kąta między tworzącą i płaszczyzną podstawy tego stożka jest równy
A) 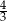 B) 12 C)
B) 12 C) 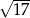 D) 4
D) 4
Stożek o średnicy podstawy 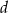 i kula o promieniu
i kula o promieniu 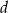 mają równe objętości. Tangens kąta między tworzącą i płaszczyzną podstawy tego stożka jest równy
mają równe objętości. Tangens kąta między tworzącą i płaszczyzną podstawy tego stożka jest równy
A) 32 B)  C)
C) 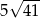 D) 4
D) 4
Powierzchnia boczna stożka o promieniu podstawy 6 cm, po rozwinięciu jest wycinkiem koła o kącie 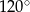 . Pole powierzchni bocznej tego stożka jest równe
. Pole powierzchni bocznej tego stożka jest równe
A) 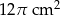 B)
B) 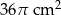 C)
C) 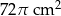 D)
D) 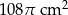
Przekrój osiowy stożka jest trójkątem równobocznym o boku  . Objętość tego stożka wyraża się wzorem
. Objętość tego stożka wyraża się wzorem
A) 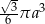 B)
B) 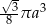 C)
C) 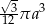 D)
D) 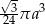
Przekrój osiowy stożka jest równoramiennym trójkątem prostokątnym o przyprostokątnej długości  . Objętość tego stożka wyraża się wzorem
. Objętość tego stożka wyraża się wzorem
A) 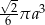 B)
B) 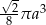 C)
C) 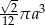 D)
D) 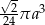
Przekrój osiowy stożka jest trójkątem prostokątnym o przeciwprostokątnej długości 6. Objętość tego stożka jest równa
A) 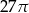 B)
B) 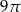 C)
C) 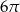 D)
D) 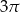
Przekrój osiowy stożka jest trójkątem prostokątnym o przeciwprostokątnej długości 8. Objętość tego stożka jest równa
A) 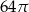 B)
B) 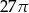 C)
C) 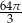 D)
D) 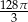
Objętość stożka wynosi 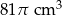 . Wysokość stożka jest 9 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego stożka jest równe
. Wysokość stożka jest 9 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego stożka jest równe
A) 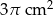 B)
B) 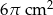 C)
C) 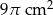 D)
D) 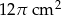
Objętość stożka wynosi 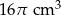 . Wysokość stożka jest 6 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego stożka jest równe
. Wysokość stożka jest 6 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego stożka jest równe
A) 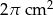 B)
B) 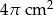 C)
C) 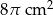 D)
D) 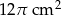
Pole powierzchni bocznej stożka wynosi 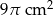 . Tworząca stożka jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego stożka jest równe
. Tworząca stożka jest 3 razy większa od promienia podstawy. Zatem pole powierzchni podstawy tego stożka jest równe
A) 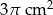 B)
B) 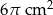 C)
C) 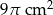 D)
D) 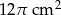
Stosunek wysokości stożka do promienia podstawy wynosi 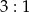 . Objętość stożka jest równa
. Objętość stożka jest równa 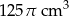 . Zatem promień podstawy stożka ma długość
. Zatem promień podstawy stożka ma długość
A) 25 cm B) 15 cm C) 5 cm D) 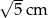
Stosunek wysokości stożka do promienia podstawy wynosi 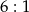 . Objętość stożka jest równa
. Objętość stożka jest równa 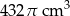 . Zatem promień podstawy stożka ma długość
. Zatem promień podstawy stożka ma długość
A) 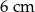 B)
B) 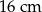 C)
C) 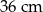 D)
D) 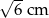
Stosunek wysokości stożka do promienia podstawy wynosi 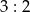 . Objętość stożka jest równa
. Objętość stożka jest równa 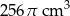 . Zatem promień podstawy stożka ma długość
. Zatem promień podstawy stożka ma długość
A) 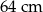 B)
B) 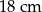 C)
C) 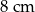 D)
D) 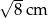
Jeśli średnica podstawy stożka jest równa 12, a wysokość stożka 8, to kąt  między wysokością stożka, a jego tworzącą jest taki, że
między wysokością stożka, a jego tworzącą jest taki, że
A) 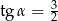 B)
B) 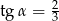 C)
C) 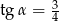 D)
D) 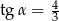
Jeśli średnica podstawy stożka jest równa 18, a wysokość stożka 12, to kąt  między wysokością stożka, a jego tworzącą jest taki, że
między wysokością stożka, a jego tworzącą jest taki, że
A) 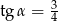 B)
B) 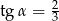 C)
C) 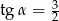 D)
D) 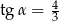
Jeśli średnica podstawy stożka jest równa 16, a wysokość stożka 6, to kąt  między wysokością stożka, a jego tworzącą jest taki, że
między wysokością stożka, a jego tworzącą jest taki, że
A) 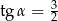 B)
B) 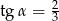 C)
C) 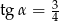 D)
D) 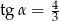
Trójkąt prostokątny równoramienny obrócono dookoła jednej z przyprostokątnych. Objętość tak otrzymanej bryły jest równa 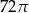 . Średnica podstawy bryły ma długość
. Średnica podstawy bryły ma długość
A) 6 B) 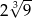 C) 12 D)
C) 12 D) 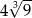
Trójkąt prostokątny równoramienny obrócono dookoła jednej z przyprostokątnych. Objętość tak otrzymanej bryły jest równa 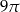 . Średnica podstawy bryły ma długość
. Średnica podstawy bryły ma długość
A) 6 B) 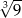 C) 3 D)
C) 3 D) 
Trójkąt prostokątny równoramienny obrócono dookoła jednej z przyprostokątnych. Objętość tak otrzymanej bryły jest równa 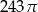 . Średnica podstawy bryły ma długość
. Średnica podstawy bryły ma długość
A) 9 B) 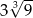 C)
C) 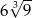 D) 18
D) 18
Kąt rozwarcia stożka ma miarę 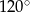 , a jego tworząca ma długość 10. Wówczas stosunek promienia podstawy stożka do jego wysokości jest równy
, a jego tworząca ma długość 10. Wówczas stosunek promienia podstawy stożka do jego wysokości jest równy
A) 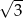 B)
B) 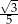 C) 5 D)
C) 5 D) 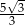
Kąt rozwarcia stożka ma miarę 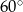 , a jego tworząca ma długość 8. Wówczas stosunek promienia podstawy stożka do jego wysokości jest równy
, a jego tworząca ma długość 8. Wówczas stosunek promienia podstawy stożka do jego wysokości jest równy
A) 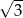 B)
B) 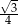 C)
C) 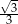 D)
D) 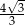
Kąt rozwarcia stożka ma miarę 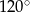 , a jego tworząca ma długość 12. Wówczas stosunek wysokości stożka do jego promienia podstawy jest równy
, a jego tworząca ma długość 12. Wówczas stosunek wysokości stożka do jego promienia podstawy jest równy
A) 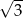 B)
B) 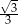 C)
C) 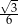 D)
D) 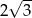
Kąt rozwarcia stożka ma miarę 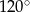 , a tworząca tego stożka ma długość 6. Promień podstawy stożka jest równy
, a tworząca tego stożka ma długość 6. Promień podstawy stożka jest równy
A) 3 B) 6 C) 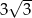 D)
D) 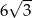
Kąt rozwarcia stożka ma miarę 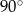 , a tworząca tego stożka ma długość 8. Promień podstawy stożka jest równy
, a tworząca tego stożka ma długość 8. Promień podstawy stożka jest równy
A) 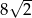 B) 4 C)
B) 4 C) 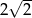 D)
D) 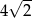
Pole podstawy stożka jest trzy razy mniejsze od jego pola powierzchni bocznej. Wówczas kąt  rozwarcia stożka spełnia warunek
rozwarcia stożka spełnia warunek
A) 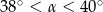 B)
B) 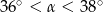 C)
C) 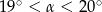 D)
D) 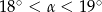
Dany jest trójkąt prostokątny o długościach boków 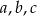 , gdzie
, gdzie 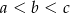 . Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt
. Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt 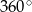 , otrzymujemy bryłę, której pole powierzchni całkowitej jest równe
, otrzymujemy bryłę, której pole powierzchni całkowitej jest równe
A) 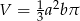 B)
B) 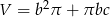 C)
C) 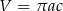 D)
D) 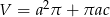
Jeśli promień podstawy stożka zwiększymy trzykrotnie, a wysokość zmniejszymy trzykrotnie, to objętość stożka
A) zwiększy się dziewięciokrotnie B) nie zmieni się
C) zwiększy się trzykrotnie D) zwiększy się sześciokrotnie
Jeśli promień podstawy stożka zwiększymy dwukrotnie, a wysokość zmniejszymy dwukrotnie, to objętość stożka
A) zwiększy się dwukrotnie B) nie zmieni się
C) zwiększy się czterokrotnie D) zmniejszy się czterokrotnie
Jeśli promień podstawy stożka zmniejszymy trzykrotnie, a wysokość zwiększymy trzykrotnie, to objętość stożka
A) zwiększy się dziewięciokrotnie B) nie zmieni się
C) zwiększy się trzykrotnie D) zmniejszy się trzykrotnie
Przekrój osiowy stożka jest trójkątem równoramiennym o ramieniu długości 12. Kąt rozwarcia stożka ma miarę 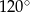 . Objętość stożka wynosi
. Objętość stożka wynosi
A) 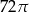 B)
B) 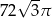 C)
C) 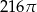 D)
D)