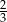Objętość stożka o wysokości 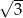 i kącie rozwarcia
i kącie rozwarcia  jest równa
jest równa
A) 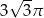 B)
B) 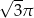 C)
C) 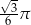 D)
D) 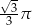
/Szkoła średnia/Zadania testowe/Geometria/Stereometria/Stożek
Kąt rozwarcia stożka ma miarę 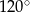 , a wysokość tego stożka ma długość 3. Objętość tego stożka jest równa
, a wysokość tego stożka ma długość 3. Objętość tego stożka jest równa
A) 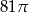 B)
B) 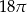 C)
C) 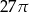 D)
D) 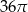
Kąt rozwarcia stożka ma miarę 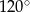 , a tworząca tego stożka ma długość 4. Objętość tego stożka jest równa
, a tworząca tego stożka ma długość 4. Objętość tego stożka jest równa
A) 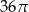 B)
B) 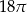 C)
C) 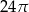 D)
D) 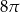
Tworząca stożka ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 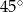 . Wysokość tego stożka jest równa
. Wysokość tego stożka jest równa
A) 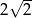 B)
B) 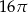 C)
C) 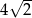 D)
D) 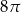
Tworząca stożka ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 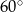 . Wysokość tego stożka jest równa
. Wysokość tego stożka jest równa
A) 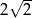 B)
B) 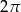 C)
C) 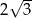 D) 2
D) 2
Tworząca stożka ma długość 4 i jest nachylona do płaszczyzny podstawy pod kątem 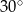 . Wysokość tego stożka jest równa
. Wysokość tego stożka jest równa
A) 2 B) 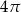 C)
C) 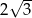 D)
D) 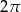
Dany jest stożek o objętości 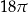 , którego przekrojem osiowym jest trójkąt
, którego przekrojem osiowym jest trójkąt 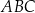 (zobacz rysunek). Kąt
(zobacz rysunek). Kąt 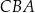 jest kątem nachylenia tworzącej
jest kątem nachylenia tworzącej 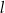 tego stożka do płaszczyzny jego podstawy. Tangens kąta
tego stożka do płaszczyzny jego podstawy. Tangens kąta 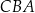 jest równy 2.
jest równy 2.
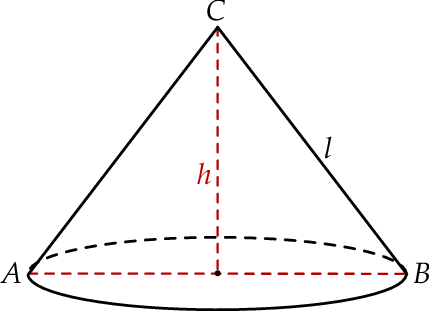
Wynika stąd, że wysokość 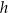 tego stożka jest równa
tego stożka jest równa
A) 12 B) 6 C) 4 D) 2
Przekrój osiowy stożka jest trójkątem równoramiennym o stosunku ramienia do podstawy 3:2. Tworząca stożka tworzy z podstawą kąt  , taki, że
, taki, że
A) 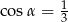 B)
B) 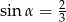 C)
C) 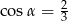 D)
D) 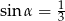
Przekrój osiowy stożka jest trójkątem równoramiennym o stosunku ramienia do podstawy 8:6. Tworząca stożka tworzy z podstawą kąt  , taki, że
, taki, że
A) 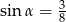 B)
B) 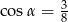 C)
C) 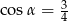 D)
D) 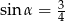
Przekrój osiowy stożka jest trójkątem równoramiennym o stosunku ramienia do podstawy 5:2. Tworząca stożka tworzy z podstawą kąt  , taki, że
, taki, że
A) 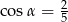 B)
B) 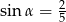 C)
C) 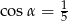 D)
D) 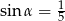
Promień podstawy stożka o objętości 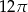 i wysokości 4 jest równy
i wysokości 4 jest równy
A) 1 B) 3 C) 6 D) 9
Tworząca stożka o promieniu podstawy 3 ma długość 6 (zobacz rysunek).
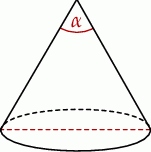
Kąt  rozwarcia tego stożka jest równy
rozwarcia tego stożka jest równy
A) 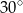 B)
B) 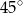 C)
C) 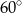 D)
D) 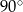
Tworząca stożka o wysokości 3 ma długość 6 (zobacz rysunek).
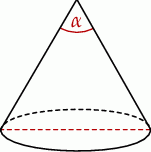
Kąt  rozwarcia tego stożka jest równy
rozwarcia tego stożka jest równy
A) 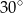 B)
B) 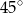 C)
C) 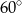 D)
D) 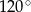
Walec i stożek mają równe promienie podstaw, a wysokość walca jest dwa razy dłuższa niż wysokość stożka. Stosunek objętości walca do objętości stożka jest równa
A) 3 B) 6 C) 2 D) 12
Walec i stożek mają równe promienie podstaw, a wysokość walca jest trzy razy dłuższa niż wysokość stożka. Stosunek objętości walca do objętości stożka jest równa
A) 9 B) 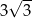 C) 3 D) 27
C) 3 D) 27
Objętość stożka o wysokości 8 i średnicy podstawy 12 jest równa
A) 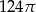 B)
B) 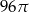 C)
C) 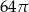 D)
D) 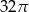
Dany jest stożek o wysokości 5 i średnicy podstawy 6. Objętość tego stożka jest równa
A) 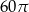 B)
B) 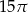 C)
C) 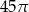 D)
D) 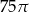
Dany jest stożek o wysokości 4 i średnicy podstawy 12. Objętość tego stożka jest równa
A) 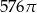 B)
B) 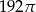 C)
C) 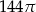 D)
D) 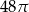
Objętość stożka o wysokości 4 i średnicy podstawy 6 jest równa
A) 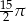 B)
B) 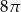 C)
C) 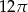 D)
D) 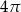
Długość tworzącej stożka jest równa 6, a obwód jego podstawy wynosi 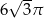 . Kąt rozwarcia tego stożka ma miarę
. Kąt rozwarcia tego stożka ma miarę
A) 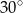 B)
B) 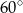 C)
C) 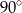 D)
D) 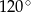
Objętość stożka o promieniu podstawy równym  jest równa
jest równa 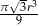 . Miara kąta rozwarcia tego stożka jest równa
. Miara kąta rozwarcia tego stożka jest równa
A) 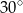 B)
B) 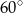 C)
C) 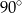 D)
D) 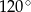
Objętość stożka o wysokości 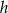 i promieniu podstawy trzy razy mniejszym od wysokości jest równa
i promieniu podstawy trzy razy mniejszym od wysokości jest równa
A) 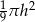 B)
B) 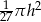 C)
C) 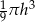 D)
D) 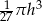
Objętość stożka o wysokości 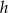 i promieniu podstawy cztery razy mniejszym od wysokości jest równa
i promieniu podstawy cztery razy mniejszym od wysokości jest równa
A) 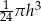 B)
B) 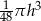 C)
C) 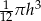 D)
D) 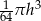
Przekrojem osiowym stożka o objętości 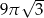 jest trójkąt równoboczny. Obwód tego trójkąta jest równy
jest trójkąt równoboczny. Obwód tego trójkąta jest równy
A) 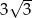 B)
B) 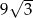 C) 18 D) 6
C) 18 D) 6
Obwód podstawy stożka wynosi 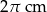 . Tworząca stożka jest 6 razy większa od promienia podstawy. Zatem pole powierzchni bocznej tego stożka jest równe
. Tworząca stożka jest 6 razy większa od promienia podstawy. Zatem pole powierzchni bocznej tego stożka jest równe
A) 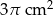 B)
B) 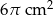 C)
C) 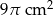 D)
D) 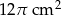
Obwód podstawy stożka wynosi 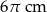 . Tworząca stożka jest 4 razy dłuższa od jego promienia podstawy. Zatem pole powierzchni całkowitej tego stożka jest równe
. Tworząca stożka jest 4 razy dłuższa od jego promienia podstawy. Zatem pole powierzchni całkowitej tego stożka jest równe
A) 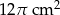 B)
B) 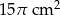 C)
C) 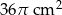 D)
D) 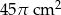
Przekrój osiowy stożka jest trójkątem równobocznym o boku  . Jeżeli
. Jeżeli  oznacza promień podstawy stożka,
oznacza promień podstawy stożka, 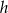 oznacza wysokość, to
oznacza wysokość, to
A) 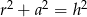 B)
B) 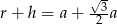 C)
C) 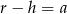 D)
D) 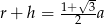
Przekrój osiowy stożka jest trójkątem równobocznym o wysokości 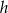 . Jeżeli
. Jeżeli  oznacza promień podstawy stożka,
oznacza promień podstawy stożka, 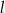 oznacza długość jego tworzącej, to
oznacza długość jego tworzącej, to
A) 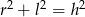 B)
B) 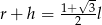 C)
C) 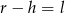 D)
D) 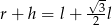
Przekrój osiowy stożka jest trójkątem rozwartokątnym o polu 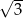 . Jeżeli tworząca tego stożka ma długość 2, to jego objętość jest równa
. Jeżeli tworząca tego stożka ma długość 2, to jego objętość jest równa
A) 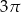 B)
B) 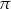 C)
C) 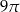 D)
D) 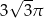
Dany jest trójkąt prostokątny o długościach boków 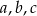 , gdzie
, gdzie 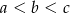 . Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt
. Obracając ten trójkąt, wokół prostej zawierającej dłuższą przyprostokątną o kąt 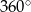 , otrzymujemy bryłę, której objętość jest równa
, otrzymujemy bryłę, której objętość jest równa
A) 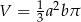 B)
B) 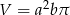 C)
C) 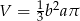 D)
D) 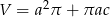
Dany jest trójkąt prostokątny o długościach boków 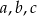 , gdzie
, gdzie 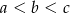 . Obracając ten trójkąt, wokół prostej zawierającej krótszą przyprostokątną o kąt
. Obracając ten trójkąt, wokół prostej zawierającej krótszą przyprostokątną o kąt 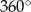 , otrzymujemy bryłę, której objętość jest równa
, otrzymujemy bryłę, której objętość jest równa
A) 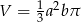 B)
B) 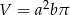 C)
C) 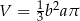 D)
D) 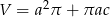
Tworząca stożka ma długość 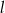 , a promień jego podstawy jest równy
, a promień jego podstawy jest równy  (zobacz rysunek).
(zobacz rysunek).
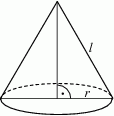
Powierzchnia boczna tego stożka jest 2 razy większa od pola jego podstawy. Wówczas
A) 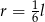 B)
B) 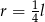 C)
C) 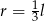 D)
D) 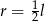
Tworząca stożka ma długość 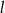 , a promień jego podstawy jest równy
, a promień jego podstawy jest równy  (zobacz rysunek).
(zobacz rysunek).
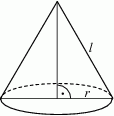
Powierzchnia boczna tego stożka jest 3 razy większa od pola jego podstawy. Wówczas
A) 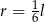 B)
B) 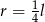 C)
C) 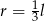 D)
D) 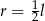
Średnica podstawy stożka ma długość 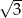 , a jego tworząca ma długość 1. Tangens kąta rozwarcia tego stożka jest równy
, a jego tworząca ma długość 1. Tangens kąta rozwarcia tego stożka jest równy
A) 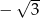 B)
B) 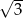 C)
C) 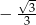 D)
D) 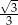
Wycinek kołowy o kącie środkowym 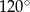 i polu
i polu 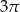 zwinięto w stożek. Promień podstawy tego stożka jest równy:
zwinięto w stożek. Promień podstawy tego stożka jest równy:
A) 2,5 B) 2 C) 1,6 D) 1
Z koła o promieniu 12 wycięto dwa wycinki odpowiadające kątom środkowym 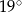 i
i 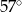 .
.
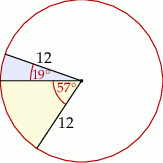
Następnie sklejono dwa stożki, których powierzchnie boczne utworzone zostały z otrzymanych wycinków. Ile razy pole podstawy większego z otrzymanych stożków jest większe od pola podstawy mniejszego stożka?
A) 3 B) 6 C) 9 D) 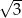
Powierzchnia boczna stożka po rozwinięciu jest półkolem o promieniu 12 cm. Podstawa tego stożka jest kołem o promieniu
A) 12 cm B) 6 cm C) 3 cm D) 1 cm
Po rozwinięciu powierzchni bocznej stożka na płaszczyźnie otrzymano jedną czwarta koła o promieniu 6. Promień podstawy tego stożka ma długość
A)  B)
B)  C) 3 D)
C) 3 D) 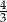
Po rozwinięciu powierzchni bocznej stożka na płaszczyźnie otrzymano połowę koła o promieniu 6. Promień podstawy tego stożka ma długość
A) 6 B)  C) 3 D)
C) 3 D)