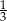W kapeluszu znajdują się króliki białe i szare. Królików szarych jest trzy razy więcej niż białych. Prawdopodobieństwo wyciągnięcia z kapelusza królika białego jest równe  . Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika szarego jest równe
. Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika szarego jest równe
A) 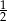 B)
B) 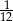 C)
C) 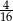 D)
D) 
/Szkoła średnia/Zadania testowe/Prawdopodobieństwo
W kapeluszu znajdują się króliki białe i szare. Prawdopodobieństwo wyciągnięcia z kapelusza królika szarego jest równe 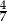 . Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika białego jest równe
. Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika białego jest równe
A)  B) 0,75 C)
B) 0,75 C)  D)
D) 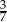
W woreczku znajdują się piłki białe i szare. Piłek szarych jest trzy razy więcej niż białych. Prawdopodobieństwo wyciągnięcia z woreczka piłki białej jest równe 0,25. Zatem prawdopodobieństwo wyciągnięcia z woreczka piłki szarej jest równe
A) 0,75 B) 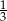 C) 0,25 D) 0,8
C) 0,25 D) 0,8
W szufladzie jest 40 koszulek, wśród których 10% jest zielonych, a pozostałe są niebieskie. Losowo wyciągamy po jednej koszulce i - bez oglądania - odkładamy do pudełka. Ile co najmniej koszulek należy wyciągnąć, aby mieć pewność, że w pudełku będą co najmniej trzy koszulki niebieskie?
A) 20 B) 10 C) 7 D) 3
W szufladzie jest 35 koszulek, wśród których 20% jest zielonych, a pozostałe są niebieskie. Losowo wyciągamy po jednej koszulce i - bez oglądania - odkładamy do pudełka. Ile co najmniej koszulek należy teraz wyciągnąć, aby mieć pewność, że w pudełku będą co najmniej trzy koszulki niebieskie?
A) 20 B) 10 C) 7 D) 3
W szufladzie jest 50 koszulek, wśród których 30% jest zielonych, a pozostałe są niebieskie. Losowo wyciągamy po jednej koszulce i - bez oglądania - odkładamy do pudełka. Ile co najmniej koszulek należy teraz wyciągnąć, aby mieć pewność, że w pudełku będzie co najmniej pięć koszulek niebieskich?
A) 20 B) 10 C) 7 D) 3
Ze zbioru liczb 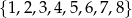 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 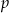 jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
jest prawdopodobieństwem wylosowania liczby podzielnej przez 3. Wtedy
A) 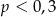 B)
B) 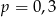 C)
C) 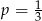 D)
D) 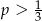
Ze zbioru liczb 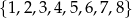 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 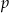 oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 3. Wtedy
oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 3. Wtedy
A) 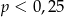 B)
B) 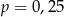 C)
C) 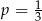 D)
D) 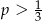
Ze zbioru liczb 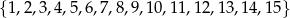 wybieramy losowo jedną liczbę. Niech
wybieramy losowo jedną liczbę. Niech 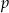 oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
A) 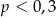 B)
B) 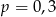 C)
C) 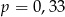 D)
D) 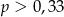
Ze zbioru liczb 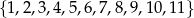 wybieramy losowo jedną liczbę. Niech
wybieramy losowo jedną liczbę. Niech 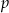 oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
oznacza prawdopodobieństwo wybrania liczby będącej wielokrotnością liczby 3. Wówczas
A) 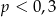 B)
B) 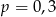 C)
C) 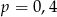 D)
D) 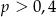
Ze zbioru 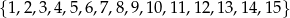 wybieramy losowo jedną liczbę. Liczba
wybieramy losowo jedną liczbę. Liczba 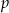 oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 4. Wówczas
oznacza prawdopodobieństwo otrzymania liczby podzielnej przez 4. Wówczas
A) 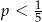 B)
B) 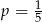 C)
C) 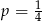 D)
D) 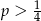
Pewnego dnia w klasie liczącej 11 dziewcząt i 15 chłopców nieobecny był jeden chłopiec i jedna dziewczynka. Nauczyciel wybrał do odpowiedzi jednego ucznia. Prawdopodobieństwo, że będzie to dziewczynka jest równe:
A) 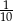 B)
B) 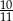 C)
C) 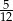 D)
D) 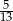
Pewnego dnia w klasie liczącej 16 dziewcząt i 12 chłopców nieobecnych było dwóch chłopców i trzy dziewczynki. Nauczyciel wybrał do odpowiedzi jednego ucznia. Prawdopodobieństwo, że będzie to dziewczynka jest równe:
A) 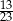 B)
B) 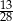 C)
C) 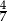 D)
D) 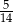
Z talii 52 kart losujemy dwa razy po jednej karcie (ze zwracaniem). Niech 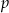 oznacza prawdopodobieństwo wylosowania dwóch królów. Wtedy
oznacza prawdopodobieństwo wylosowania dwóch królów. Wtedy
A) 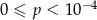 B)
B) 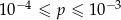 C)
C) 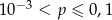 D)
D) 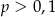
Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo zdarzenia polegającego na tym, że wynikiem rzutu są dwa orły i sześć oczek na kostce, jest równe
A) 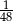 B)
B) 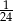 C)
C) 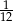 D)
D) 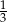
Doświadczenie losowe polega na rzucie dwiema symetrycznymi monetami i sześcienną kostką do gry. Prawdopodobieństwo zdarzenia polegającego na tym, że wynikiem rzutu jest co najmniej jedna reszka i trzy oczka na kostce, jest równe
A) 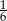 B)
B) 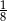 C)
C) 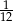 D)
D) 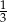
Prawdopodobieństwo zdarzenia 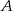 jest 6 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do
jest 6 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do 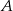 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 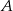 jest równe
jest równe
A) 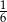 B)
B)  C)
C) 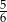 D)
D) 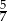
Jeżeli prawdopodobieństwo zdarzenia losowego 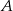 jest 5 razy większe od prawdopodobieństwa zdarzenia przeciwnego do zdarzenia
jest 5 razy większe od prawdopodobieństwa zdarzenia przeciwnego do zdarzenia 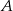 , to prawdopodobieństwo zdarzenia
, to prawdopodobieństwo zdarzenia 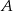 jest równe
jest równe
A) 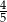 B)
B) 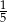 C)
C) 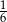 D)
D) 
Prawdopodobieństwo zdarzenia 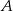 jest 6 razy większe niż prawdopodobieństwo zdarzenia przeciwnego do
jest 6 razy większe niż prawdopodobieństwo zdarzenia przeciwnego do 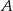 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 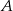 jest równe
jest równe
A) 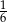 B)
B)  C)
C) 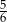 D)
D) 
Prawdopodobieństwo zdarzenia 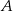 jest 5 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do
jest 5 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do 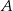 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 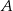 jest równe
jest równe
A)  B)
B) 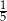 C)
C)  D)
D) 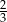
Jeżeli 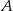 jest zdarzeniem losowym, a
jest zdarzeniem losowym, a 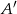 – zdarzeniem przeciwnym do zdarzenia
– zdarzeniem przeciwnym do zdarzenia 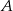 oraz zachodzi równość
oraz zachodzi równość 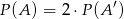 , to
, to
A) 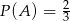 B)
B) 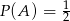 C)
C) 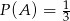 D)
D) 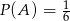
Jeżeli 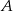 jest zdarzeniem losowym oraz
jest zdarzeniem losowym oraz 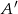 jest zdarzeniem przeciwnym do zdarzenia
jest zdarzeniem przeciwnym do zdarzenia 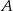 i
i 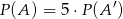 , to prawdopodobieństwo zdarzenia
, to prawdopodobieństwo zdarzenia 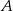 jest równe
jest równe
A) 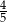 B)
B) 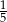 C)
C) 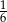 D)
D) 
Prawdopodobieństwo zdarzenia 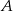 jest 7 razy większe niż prawdopodobieństwo zdarzenia przeciwnego do
jest 7 razy większe niż prawdopodobieństwo zdarzenia przeciwnego do 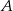 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 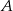 jest równe
jest równe
A)  B)
B)  C)
C) 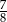 D)
D) 
Prawdopodobieństwo zdarzenia 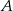 jest 3 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do
jest 3 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do 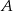 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 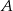 jest równe
jest równe
A) 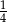 B)
B) 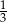 C)
C) 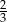 D)
D) 
Doświadczenie losowe polega na czterokrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn liczb wyrzuconych oczek jest liczbą nieparzystą, jest równe
A) 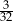 B)
B) 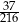 C)
C) 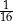 D)
D) 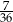
Jacek bierze udział w olimpiadzie chemicznej i olimpiadzie matematycznej. Prawdopodobieństwo, że zostanie laureatem olimpiady chemicznej jest równe 0,3, a prawdopodobieństwo, że zostanie laureatem przynajmniej jednej z tych dwóch olimpiad wynosi 0,72. Prawdopodobieństwo, że będzie laureatem obu olimpiad jest równe 0,18. Zatem prawdopodobieństwo, że będzie laureatem olimpiady matematycznej jest równe
A) 0,1 B) 0,6 C) 0,7 D) 0,4
Ania bierze udział w olimpiadzie biologicznej i olimpiadzie fizycznej. Prawdopodobieństwo, że zostanie laureatką olimpiady biologicznej jest równe 0,4, a prawdopodobieństwo, że zostanie laureatką przynajmniej jednej z tych dwóch olimpiad wynosi 0,62. Prawdopodobieństwo, że będzie laureatką obu olimpiad jest równe 0,18. Zatem prawdopodobieństwo, że będzie laureatką olimpiady fizycznej jest równe
A) 0,4 B) 0,3 C) 0,5 D) 0,2
Tomek bierze udział w olimpiadzie fizycznej i olimpiadzie matematycznej. Prawdopodobieństwo, że zostanie laureatem olimpiady fizycznej jest równe 0,5, a prawdopodobieństwo, że zostanie laureatem przynajmniej jednej z tych dwóch olimpiad wynosi 0,74. Prawdopodobieństwo, że będzie laureatem obu olimpiad jest równe 0,26. Zatem prawdopodobieństwo, że będzie laureatem olimpiady matematycznej jest równe
A) 0,5 B) 0,6 C) 0,7 D) 0,4
Z pudełka zawierającego dwa rodzaje monet wybieramy losowo dwie. Prawdopodobieństwo wybrania co najmniej jednej monety dwuzłotowej jest równe 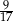 , a prawdopodobieństwo wybrania co najmniej jednej monety pięciozłotowej jest równe
, a prawdopodobieństwo wybrania co najmniej jednej monety pięciozłotowej jest równe 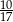 . Zatem prawdopodobieństwo wybrania dokładnie jednej monety dwuzłotowej jest równe
. Zatem prawdopodobieństwo wybrania dokładnie jednej monety dwuzłotowej jest równe
A) 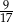 B)
B) 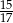 C)
C) 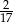 D)
D) 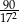
Ze zbioru liczb 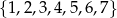 losujemy kolejno dwa razy po jednej cyfrze bez zwracania. Zapisując wylosowane cyfry w kolejności losowania, otrzymujemy liczbę dwucyfrową. Prawdopodobieństwo otrzymania liczby większej od 32 jest równe
losujemy kolejno dwa razy po jednej cyfrze bez zwracania. Zapisując wylosowane cyfry w kolejności losowania, otrzymujemy liczbę dwucyfrową. Prawdopodobieństwo otrzymania liczby większej od 32 jest równe
A) 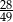 B)
B) 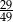 C)
C) 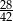 D)
D) 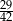
Ze zbioru cyfr 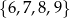 losujemy kolejno bez zwracania dwie cyfry i tworzymy liczbę dwucyfrową. Prawdopodobieństwo tego, że utworzona liczba będzie nie mniejsza niż 89 jest równe
losujemy kolejno bez zwracania dwie cyfry i tworzymy liczbę dwucyfrową. Prawdopodobieństwo tego, że utworzona liczba będzie nie mniejsza niż 89 jest równe
A) 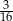 B)
B)  C)
C) 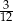 D)
D) 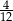
Losujemy jedną liczbę trzycyfrową. Prawdopodobieństwo 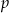 otrzymania liczby, której cyfry to 1,2,3 (w dowolnej kolejności) spełnia warunek
otrzymania liczby, której cyfry to 1,2,3 (w dowolnej kolejności) spełnia warunek
A) 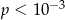 B)
B) 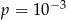 C)
C) 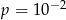 D)
D) 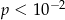
Losujemy jedną liczbę czterocyfrową. Prawdopodobieństwo 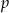 otrzymania liczby, której cyfry to 1,1,2,2 (w dowolnej kolejności) spełnia warunek
otrzymania liczby, której cyfry to 1,1,2,2 (w dowolnej kolejności) spełnia warunek
A) 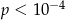 B)
B) 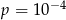 C)
C) 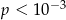 D)
D) 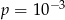
O zdarzeniach losowych 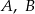 wiadomo, że:
wiadomo, że: 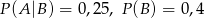 i
i 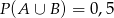 . Wtedy prawdopodobieństwo
. Wtedy prawdopodobieństwo 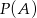 jest równe
jest równe
A) 0,1 B) 0,2 C) 0,3 D) 0,4
Ze zbioru dwudziestu czterech kolejnych liczb naturalnych od 1 do 24 losujemy jedną liczbę. Niech 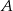 oznacza zdarzenie, że wylosowana liczba będzie dzielnikiem liczby 24. Wtedy prawdopodobieństwo zdarzenia
oznacza zdarzenie, że wylosowana liczba będzie dzielnikiem liczby 24. Wtedy prawdopodobieństwo zdarzenia 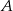 jest równe
jest równe
A) 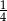 B)
B) 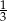 C)
C) 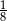 D)
D) 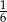
Ze zbioru trzydziestu kolejnych liczb naturalnych od 1 do 30 losujemy jedną liczbę. Niech 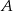 oznacza zdarzenie, że wylosowana liczba będzie dzielnikiem liczby 30. Wtedy prawdopodobieństwo zdarzenia
oznacza zdarzenie, że wylosowana liczba będzie dzielnikiem liczby 30. Wtedy prawdopodobieństwo zdarzenia 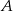 jest równe
jest równe
A) 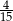 B)
B) 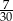 C)
C) 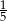 D)
D) 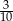
Jacek i Karol rzucają śnieżkami do celu. Jacek trafia do celu średnio trzy razy na dziesięć rzutów, a Karol trafia do celu średnio raz na pięć rzutów. Prawdopodobieństwo, że cel zostanie trafiony dokładnie raz, jeżeli każdy z chłopców wykona po jednym rzucie jest równe
A) 0,06 B) 0,38 C) 0,56 D) 0,5
Ewa i Kasia rzucają śnieżkami do celu. Ewa trafia do celu średnio raz na pięć rzutów, a Kasia trafia do celu średnio trzy razy na dziesięć rzutów. Prawdopodobieństwo, że cel zostanie trafiony dokładnie raz, jeżeli każda z dziewcząt wykona po jednym rzucie jest równe
A) 0,5 B) 0,56 C) 0,38 D) 0,06
W pewnej loterii fantowej przygotowano dwie urny z losami, przy czym w drugiej urnie było trzy razy więcej losów niż w pierwszej urnie. Prawdopodobieństwo wybrania losu wygrywającego z pierwszej urny jest równe 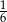 , a prawdopodobieństwo wybrania losu wygrywającego z drugiej urny jest równe
, a prawdopodobieństwo wybrania losu wygrywającego z drugiej urny jest równe 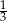 . Przed rozpoczęciem loterii losy z obu urn zmieszano i umieszczono w jednej urnie. Po tej operacji prawdopodobieństwo wybrania losu wygrywającego jest równe
. Przed rozpoczęciem loterii losy z obu urn zmieszano i umieszczono w jednej urnie. Po tej operacji prawdopodobieństwo wybrania losu wygrywającego jest równe
A) 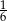 B)
B) 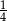 C)
C) 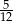 D)
D) 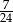
W pewnej loterii fantowej przygotowano dwie urny z losami, przy czym w drugiej urnie było trzy razy więcej losów niż w pierwszej urnie. Prawdopodobieństwo wybrania losu wygrywającego z pierwszej urny jest równe  , a prawdopodobieństwo wybrania losu wygrywającego z drugiej urny jest równe
, a prawdopodobieństwo wybrania losu wygrywającego z drugiej urny jest równe 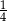 . Przed rozpoczęciem loterii losy z obu urn zmieszano i umieszczono w jednej urnie. Po tej operacji prawdopodobieństwo wybrania losu wygrywającego jest równe
. Przed rozpoczęciem loterii losy z obu urn zmieszano i umieszczono w jednej urnie. Po tej operacji prawdopodobieństwo wybrania losu wygrywającego jest równe
A) 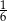 B)
B) 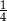 C)
C) 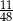 D)
D) 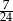
W grupie 24 osób (mężczyzn i kobiet) jest 3 razy więcej kobiet niż mężczyzn. Z grupy tej losujemy 2 osoby. Prawdopodobieństwo wylosowania każdej osoby jest takie samo. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosowano osoby różnej płci to
A) 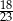 B)
B)  C)
C) 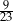 D)
D)