Punkt 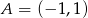 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 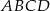 , którego bok
, którego bok 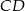 zawiera się w prostej
zawiera się w prostej 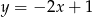 . Podstawa
. Podstawa 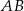 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 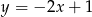 B)
B) 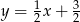 C)
C) 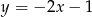 D)
D) 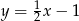
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Czworokąt
Punkt 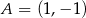 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 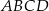 , którego bok
, którego bok 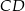 zawiera się w prostej
zawiera się w prostej 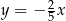 . Podstawa
. Podstawa  zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 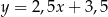 B)
B) 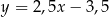 C)
C) 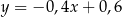 D)
D) 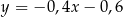
Punkt 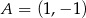 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 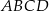 , którego bok
, którego bok 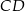 zawiera się w prostej
zawiera się w prostej 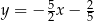 . Podstawa
. Podstawa 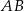 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A)  B)
B) 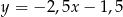 C)
C) 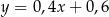 D)
D) 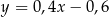
Boki równoległoboku są zawarte w prostych o równaniach: 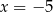 ,
, 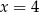 ,
, 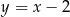 ,
, 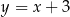 . Pole tego równoległoboku jest równe
. Pole tego równoległoboku jest równe
A) 45 B) 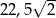 C)
C) 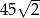 D) 22,5
D) 22,5
Punkty: 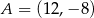 ,
, 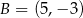 ,
, 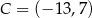 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku  . Wierzchołek
. Wierzchołek 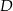 tego równoległoboku ma współrzędne
tego równoległoboku ma współrzędne
A) 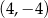 B)
B) 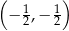 C)
C) 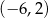 D)
D) 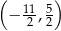
Punkty 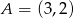 i
i 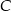 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 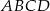 , a punkt
, a punkt 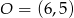 jest środkiem okręgu opisanego na tym kwadracie. Współrzędne punktu
jest środkiem okręgu opisanego na tym kwadracie. Współrzędne punktu 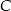 są równe
są równe
A) 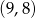 B)
B) 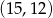 C)
C) 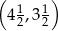 D)
D) 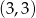
Jedna z przekątnych kwadratu 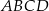 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 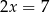 oraz
oraz 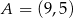 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 121 B) 24,5 C) 60,5 D) 49
Dwusieczne kątów utworzonych przez przekątne prostokąta 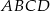 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 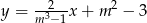 oraz
oraz 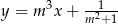 . Zatem
. Zatem
A) 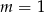 B)
B) 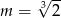 C)
C) 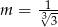 D)
D) 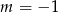
Punkty 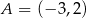 i
i 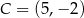 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 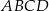 . Długość przekątnej
. Długość przekątnej 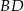 tego prostokąta jest równa
tego prostokąta jest równa
A) 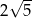 B)
B) 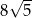 C)
C) 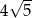 D)
D) 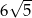
Punkt 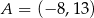 jest wierzchołkiem kwadratu
jest wierzchołkiem kwadratu  , którego przekątne przecinają się w punkcie
, którego przekątne przecinają się w punkcie 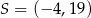 . Punkty
. Punkty  i
i 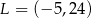 są odpowiednio środkami odcinków
są odpowiednio środkami odcinków 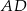 i
i 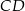 . Punkt
. Punkt 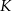 ma współrzędne
ma współrzędne
A) 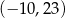 B)
B) 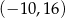 C)
C) 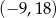 D)
D) 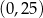
W układzie współrzędnych dany jest równoległobok 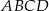 o wierzchołkach
o wierzchołkach 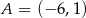 ,
, 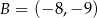 ,
, 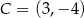 i
i 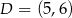 . Środek tego równoległoboku jest w tej samej ćwiartce, co wierzchołek
. Środek tego równoległoboku jest w tej samej ćwiartce, co wierzchołek
A) 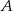 B)
B) 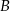 C)
C) 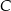 D)
D) 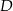
Podstawa 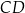 trapezu
trapezu 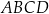 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 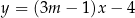 . Wierzchołki
. Wierzchołki 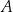 i
i 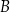 tego trapezu mają odpowiednio współrzędne
tego trapezu mają odpowiednio współrzędne 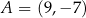 i
i 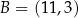 . Liczba
. Liczba 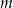 jest zatem równa
jest zatem równa
A) 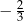 B) 2 C)
B) 2 C) 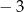 D)
D) 
W prostokącie 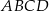 dane są wierzchołki
dane są wierzchołki 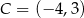 oraz
oraz 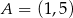 . Bok
. Bok 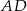 ma długość 3. Pole tego prostokąta jest równe
ma długość 3. Pole tego prostokąta jest równe
A) 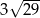 B)
B) 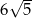 C) 24 D) 18
C) 24 D) 18
W prostokącie 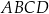 dane są wierzchołki
dane są wierzchołki 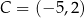 oraz
oraz 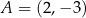 . Bok
. Bok 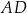 ma długość 5. Pole tego prostokąta jest równe
ma długość 5. Pole tego prostokąta jest równe
A) 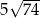 B) 35 C)
B) 35 C) 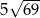 D) 245
D) 245
Punkt 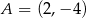 jest wierzchołkiem prostokąta
jest wierzchołkiem prostokąta 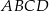 . Prosta o równaniu
. Prosta o równaniu 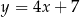 zawiera bok
zawiera bok 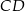 . Bok
. Bok 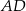 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 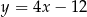 B)
B) 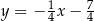 C)
C) 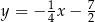 D)
D) 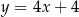
W trapez 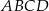 wpisano koło
wpisano koło 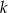 , które jest styczne do podstaw trapezu w punktach
, które jest styczne do podstaw trapezu w punktach 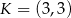 i
i 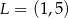 . Pole koła
. Pole koła 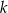 jest równe
jest równe
A) 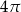 B)
B) 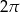 C)
C) 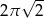 D)
D) 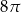
Punkty 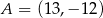 i
i 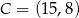 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 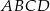 . Przekątne tego kwadratu przecinają się w punkcie
. Przekątne tego kwadratu przecinają się w punkcie
A) 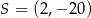 B)
B) 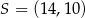 C)
C) 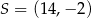 D)
D) 
Punkty 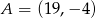 i
i 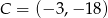 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 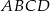 . Przekątne tego kwadratu przecinają się w punkcie
. Przekątne tego kwadratu przecinają się w punkcie
A) 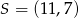 B)
B) 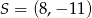 C)
C) 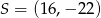 D)
D) 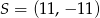
Punkty 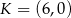 ,
, 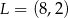 i
i 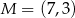 to środki boków, odpowiednio
to środki boków, odpowiednio 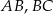 i
i 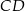 równoległoboku
równoległoboku 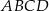 . Różnica długości przekątnych tego równoległoboku jest równa
. Różnica długości przekątnych tego równoległoboku jest równa
A) 4 B) 2 C) 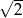 D)
D) 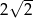
Punkty 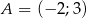 ,
, 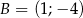 ,
, 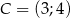 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 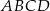 . Równanie prostej zawierającej bok
. Równanie prostej zawierającej bok 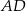 tego równoległoboku ma postać
tego równoległoboku ma postać
A) 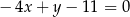 B)
B) 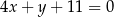
C) 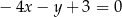 D)
D) 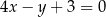
Na płaszczyźnie dany jest czworokąt 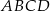 .
.
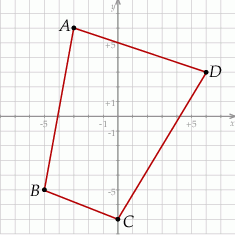
Który wierzchołek tego czworokąta jest położony najdalej od początku układu współrzędnych?
A) 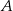 B)
B) 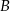 C)
C)  D)
D) 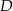
Przekątne rombu 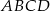 są zawarte w prostych o równaniach:
są zawarte w prostych o równaniach: 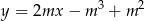 oraz
oraz 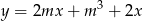 . Zatem
. Zatem
A) 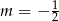 B)
B) 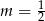 C)
C) 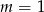 D)
D) 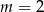
Boki równoległoboku 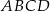 zwierają się w prostych o równaniach:
zwierają się w prostych o równaniach:
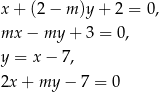
Zatem
A) 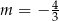 B)
B) 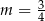 C)
C) 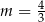 D)
D) 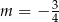
Bok 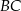 kwadratu
kwadratu 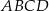 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu 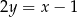 . Bok
. Bok 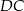 kwadratu
kwadratu 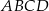 może zawierać się w prostej o równaniu
może zawierać się w prostej o równaniu
A) 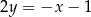 B)
B) 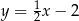 C)
C) 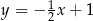 D)
D) 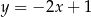
Punkty 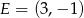 i
i 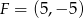 są środkami dwóch sąsiednich boków kwadratu
są środkami dwóch sąsiednich boków kwadratu 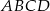 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 10 B) 25 C) 40 D) 100

