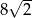Dany jest prostokąt 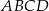 o wierzchołkach
o wierzchołkach 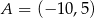 ,
, 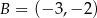 ,
, 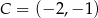 i
i 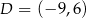 . Który z podanych punktów leży na okręgu opisanym na prostokącie
. Który z podanych punktów leży na okręgu opisanym na prostokącie 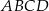 ?
?
A) 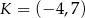 B)
B) 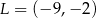 C)
C) 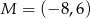 D)
D) 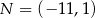
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Czworokąt
Równanie okręgu wpisanego w romb o wierzchołkach 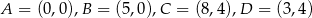 ma postać
ma postać
A) 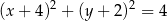 B)
B) 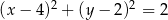
C) 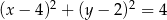 D)
D) 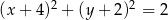
Równanie okręgu wpisanego w romb o wierzchołkach 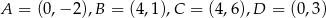 ma postać
ma postać
A) 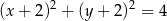 B)
B) 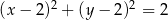
C) 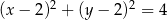 D)
D) 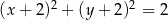
Dane są trzy niewspółliniowe punkty: 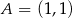 ,
, 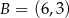 ,
, 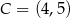 . Ile jest wszystkich punktów
. Ile jest wszystkich punktów 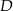 takich, że czworokąt o wierzchołkach w punktach
takich, że czworokąt o wierzchołkach w punktach 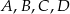 jest równoległobokiem?
jest równoległobokiem?
A) 1 B) 2 C) 3 D) 4
Punkty 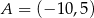 ,
, 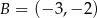 i
i 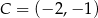 są kolejnymi wierzchołkami prostokąta
są kolejnymi wierzchołkami prostokąta 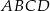 . Wierzchołek
. Wierzchołek 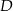 tego prostokąta ma współrzędne
tego prostokąta ma współrzędne
A) 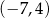 B)
B) 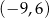 C)
C) 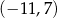 D)
D) 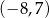
W układzie współrzędnych zaznaczono trzy kolejne wierzchołki prostokąta 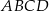 :
: 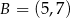 ,
, 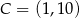 ,
, 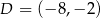 . Jakie współrzędne ma punkt A?
. Jakie współrzędne ma punkt A?
A) 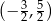 B)
B) 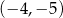 C)
C) 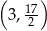 D)
D) 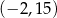
Boki 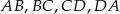 czworokąta
czworokąta  są odpowiednio zawarte w prostych o równaniach
są odpowiednio zawarte w prostych o równaniach 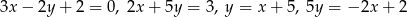 . Wtedy czworokąt
. Wtedy czworokąt 
A) jest równoległobokiem, który nie jest rombem
B) jest rombem
C) jest trapezem, który nie jest równoległobokiem
D) nie jest trapezem
Punkty 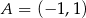 i
i 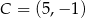 są wierzchołkami rombu
są wierzchołkami rombu 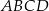 , a prosta określona równaniem
, a prosta określona równaniem 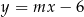 zawiera przekątną
zawiera przekątną 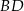 tego rombu. Wynika stąd, że
tego rombu. Wynika stąd, że
A) 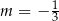 B)
B) 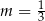 C)
C) 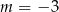 D)
D) 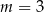
Punkty 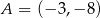 i
i 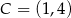 są wierzchołkami rombu
są wierzchołkami rombu 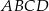 . Wierzchołki
. Wierzchołki 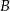 i
i 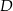 tego rombu są zawarte w prostej o równaniu
tego rombu są zawarte w prostej o równaniu 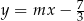 . Zatem
. Zatem
A) 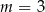 B)
B) 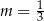 C)
C) 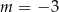 D)
D) 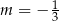
Punkty 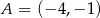 i
i 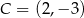 są wierzchołkami rombu
są wierzchołkami rombu 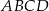 . Wierzchołki
. Wierzchołki 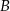 i
i 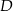 tego rombu są zawarte w prostej o równaniu
tego rombu są zawarte w prostej o równaniu 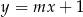 . Zatem
. Zatem
A) 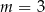 B)
B) 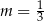 C)
C) 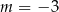 D)
D) 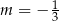
Punkt 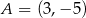 jest wierzchołkiem kwadratu
jest wierzchołkiem kwadratu 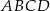 , a punkt
, a punkt 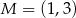 jest punktem przecięcia się przekątnych tego kwadratu. Wynika stąd, że pole kwadratu
jest punktem przecięcia się przekątnych tego kwadratu. Wynika stąd, że pole kwadratu 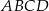 jest równe
jest równe
A) 68 B) 136 C) 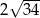 D)
D) 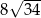
Punkt 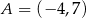 jest wierzchołkiem kwadratu
jest wierzchołkiem kwadratu 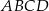 , a punkt
, a punkt 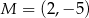 jest punktem przecięcia się przekątnych tego kwadratu. Wynika stąd, że pole kwadratu
jest punktem przecięcia się przekątnych tego kwadratu. Wynika stąd, że pole kwadratu 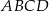 jest równe
jest równe
A) 360 B) 90 C) 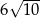 D)
D) 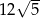
Punkt 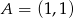 jest wierzchołkiem rombu
jest wierzchołkiem rombu 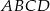 . Prosta o równaniu
. Prosta o równaniu 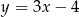 zawiera przekątną
zawiera przekątną 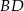 . Przekątna
. Przekątna 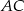 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 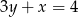 B)
B) 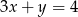 C)
C) 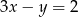 D)
D) 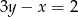
Punkt 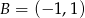 jest wierzchołkiem rombu
jest wierzchołkiem rombu 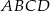 . Prosta o równaniu
. Prosta o równaniu 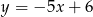 zwiera przekątną
zwiera przekątną 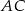 . Przekątna
. Przekątna 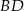 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 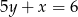 B)
B) 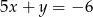 C)
C) 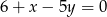 D)
D) 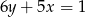
W kartezjańskim układzie współrzędnych 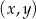 dany jest kwadrat
dany jest kwadrat 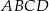 . Wierzchołki
. Wierzchołki 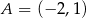 i
i 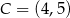 są końcami przekątnej tego kwadratu. Długość przekątnej kwadratu
są końcami przekątnej tego kwadratu. Długość przekątnej kwadratu 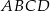 jest równa
jest równa
A) 10 B) 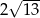 C)
C) 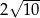 D) 8
D) 8
W kartezjańskim układzie współrzędnych 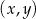 dany jest kwadrat
dany jest kwadrat 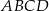 . Wierzchołki
. Wierzchołki 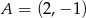 i
i 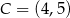 są końcami przekątnej tego kwadratu. Długość przekątnej kwadratu
są końcami przekątnej tego kwadratu. Długość przekątnej kwadratu 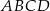 jest równa
jest równa
A) 10 B) 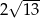 C)
C) 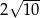 D) 8
D) 8
Oś 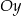 kartezjańskiego układu współrzędnych jest osią symetrii czworokąta
kartezjańskiego układu współrzędnych jest osią symetrii czworokąta 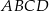 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Środek jednej z przekątnych czworokąta 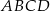 musi leżeć na osi musi leżeć na osi 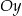 . . | P | F |
Czworokąt  musi być trapezem. musi być trapezem. | P | F |
W kartezjańskim układzie współrzędnych 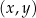 punkt
punkt 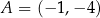 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 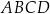 . Punkt
. Punkt 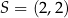 jest środkiem symetrii tego równoległoboku. Długość przekątnej
jest środkiem symetrii tego równoległoboku. Długość przekątnej 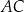 równoległoboku
równoległoboku 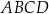 jest równa
jest równa
A) 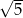 B)
B) 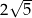 C)
C) 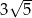 D)
D) 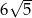
W kartezjańskim układzie współrzędnych 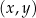 punkt
punkt 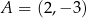 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 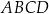 . Punkt
. Punkt 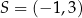 jest środkiem symetrii tego równoległoboku. Długość przekątnej
jest środkiem symetrii tego równoległoboku. Długość przekątnej 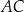 równoległoboku
równoległoboku 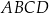 jest równa
jest równa
A) 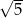 B)
B) 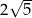 C)
C) 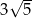 D)
D) 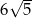
Punkt 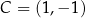 jest wierzchołkiem trapezu
jest wierzchołkiem trapezu 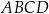 . Prosta o równaniu
. Prosta o równaniu 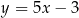 zawiera podstawę
zawiera podstawę 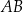 . Podstawa
. Podstawa 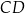 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 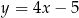 B)
B) 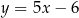 C)
C) 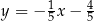 D)
D) 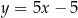
Punkt 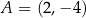 jest wierzchołkiem trapezu
jest wierzchołkiem trapezu 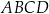 . Prosta o równaniu
. Prosta o równaniu 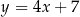 zawiera podstawę
zawiera podstawę 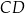 . Podstawa
. Podstawa 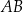 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 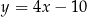 B)
B) 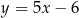 C)
C) 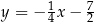 D)
D) 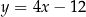
Punkt 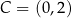 jest wierzchołkiem trapezu
jest wierzchołkiem trapezu 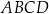 , którego podstawa
, którego podstawa 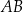 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 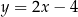 . Wskaż równanie prostej zawierającej podstawę
. Wskaż równanie prostej zawierającej podstawę 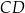 .
.
A) 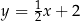 B)
B) 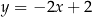 C)
C) 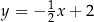 D)
D) 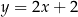
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 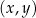 , dany jest trapez
, dany jest trapez 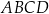 , w którym boki
, w którym boki 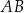 i
i 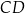 są równoległe oraz
są równoległe oraz 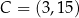 . Wierzchołki
. Wierzchołki 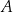 i
i 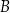 tego trapezu leżą na prostej o równaniu
tego trapezu leżą na prostej o równaniu 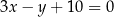 . Bok
. Bok 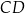 tego trapezu zawiera się w prostej o równaniu
tego trapezu zawiera się w prostej o równaniu
A) 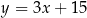 B)
B) 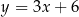 C)
C) 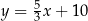 D)
D) 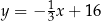
Dany jest trapez 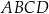 , w którym boki
, w którym boki 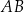 i
i 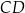 są równoległe oraz
są równoległe oraz 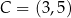 . Wierzchołki
. Wierzchołki 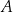 i
i 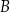 tego trapezu leżą na prostej o równaniu
tego trapezu leżą na prostej o równaniu 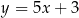 . Wtedy bok
. Wtedy bok 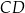 tego trapezu zawiera się w prostej o równaniu
tego trapezu zawiera się w prostej o równaniu
A) 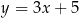 B)
B) 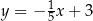 C)
C) 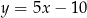 D)
D) 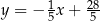
Punkty 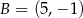 i
i 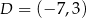 są wierzchołkami rombu
są wierzchołkami rombu 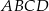 . Współczynnik kierunkowy przekątnej
. Współczynnik kierunkowy przekątnej 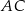 tego rombu jest równy
tego rombu jest równy
A) 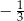 B) 3 C)
B) 3 C) 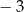 D)
D) 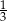
Przeciwległe wierzchołki kwadratu 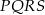 mają współrzędne
mają współrzędne 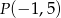 oraz
oraz 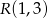 . Wobec tego obwód kwadratu wynosi
. Wobec tego obwód kwadratu wynosi
A) 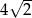 B)
B) 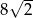 C) 8 D) 4
C) 8 D) 4
Obwód kwadratu, którego przeciwległe wierzchołki mają współrzędne 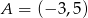 i
i 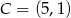 jest równy
jest równy
A) 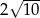 B)
B) 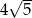 C)
C)  D)
D) 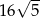
Przeciwległe wierzchołki kwadratu 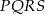 mają współrzędne
mają współrzędne 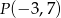 oraz
oraz 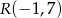 . Wobec tego obwód kwadratu wynosi
. Wobec tego obwód kwadratu wynosi
A) 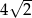 B)
B) 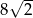 C) 8 D) 4
C) 8 D) 4
Przeciwległe wierzchołki kwadratu 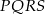 mają współrzędne
mają współrzędne 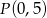 oraz
oraz 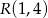 . Wobec tego obwód kwadratu wynosi
. Wobec tego obwód kwadratu wynosi
A) 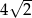 B)
B) 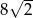 C) 8 D) 4
C) 8 D) 4
Obwód równoległoboku 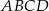 o wierzchołkach
o wierzchołkach 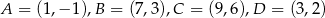 jest równy
jest równy
A) 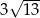 B)
B) 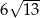 C)
C) 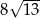 D)
D) 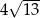
Obwód równoległoboku 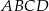 o wierzchołkach
o wierzchołkach 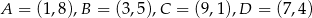 jest równy
jest równy
A) 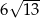 B)
B) 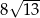 C)
C) 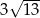 D)
D) 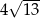
Dane są trzy niewspółliniowe punkty: 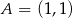 ,
, 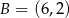 ,
, 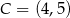 . Ile jest wszystkich punktów
. Ile jest wszystkich punktów 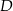 takich, że czworokąt o wierzchołkach w punktach
takich, że czworokąt o wierzchołkach w punktach  jest trapezem prostokątnym?
jest trapezem prostokątnym?
A) 1 B) 3 C) 6 D) 4
Punkty 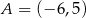 ,
, 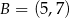 ,
, 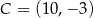 są wierzchołkami równoległoboku
są wierzchołkami równoległoboku 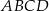 . Długość przekątnej
. Długość przekątnej 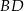 tego równoległoboku jest równa
tego równoległoboku jest równa
A) 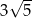 B)
B) 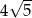 C)
C) 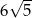 D)
D) 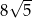
Punkty 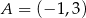 i
i 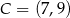 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 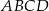 . Promień okręgu opisanego na tym prostokącie jest równy
. Promień okręgu opisanego na tym prostokącie jest równy
A) 10 B) 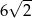 C) 5 D)
C) 5 D) 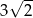
Punkty 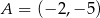 i
i 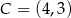 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 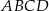 . Promień okręgu opisanego na tym prostokącie jest równy
. Promień okręgu opisanego na tym prostokącie jest równy
A) 8 B) 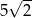 C) 5 D)
C) 5 D) 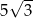
Punkty 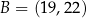 i
i 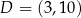 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 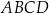 . Promień okręgu opisanego na tym prostokącie jest równy
. Promień okręgu opisanego na tym prostokącie jest równy
A) 20 B) 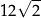 C) 10 D)
C) 10 D) 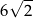
Punkty 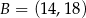 i
i 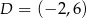 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 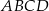 . Promień okręgu opisanego na tym prostokącie jest równy
. Promień okręgu opisanego na tym prostokącie jest równy
A) 10 B) 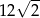 C) 20 D)
C) 20 D) 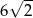
Punkty 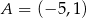 i
i 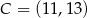 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 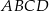 . Promień okręgu opisanego na tym prostokącie jest równy
. Promień okręgu opisanego na tym prostokącie jest równy
A) 10 B) 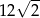 C) 20 D)
C) 20 D) 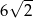
Punkty 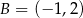 i
i 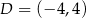 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 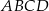 . Promień okręgu opisanego na tym prostokącie jest równy
. Promień okręgu opisanego na tym prostokącie jest równy
A) 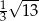 B)
B) 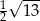 C)
C) 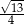 D)
D) 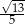
Punkt 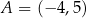 jest wierzchołkiem równoległoboku
jest wierzchołkiem równoległoboku 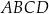 . Przekątne tego równoległoboku przecinają się w punkcie
. Przekątne tego równoległoboku przecinają się w punkcie 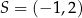 . Wierzchołek
. Wierzchołek 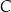 ma współrzędne
ma współrzędne
A) 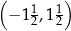 B)
B) 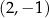 C)
C) 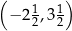 D)
D) 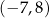
Kwadrat 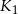 o wierzchołkach
o wierzchołkach 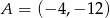 ,
, 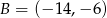 ,
, 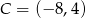 i
i 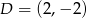 przekształcono w symetrii względem osi
przekształcono w symetrii względem osi 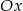 i otrzymano kwadrat
i otrzymano kwadrat 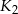 . Odległość między środkami kwadratów
. Odległość między środkami kwadratów 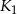 i
i 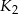 jest równa
jest równa
A) 4 B) 8 C) 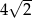 D)
D)