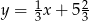Punkty 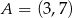 i
i 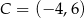 są końcami przekątnej kwadratu
są końcami przekątnej kwadratu 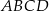 . Promień okręgu opisanego na tym kwadracie jest równy
. Promień okręgu opisanego na tym kwadracie jest równy
A) 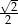 B)
B)  C)
C) 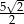 D) 5
D) 5
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Czworokąt
Punkty 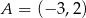 i
i 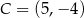 są końcami przekątnej kwadratu
są końcami przekątnej kwadratu 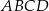 . Promień okręgu opisanego na tym kwadracie jest równy
. Promień okręgu opisanego na tym kwadracie jest równy
A) 100 B) 50 C) 10 D) 5
Dwa przeciwległe wierzchołki prostokąta mają współrzędne 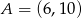 i
i 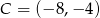 . Środek okręgu opisanego na tym prostokącie leży na prostej
. Środek okręgu opisanego na tym prostokącie leży na prostej
A) 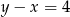 B)
B) 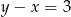 C)
C) 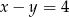 D)
D) 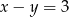
Punkty 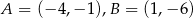 i
i 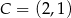 są trzema kolejnymi wierzchołkami rombu
są trzema kolejnymi wierzchołkami rombu 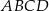 . Pole tego rombu jest równe
. Pole tego rombu jest równe
A) 40 B) 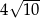 C) 80 D) 20
C) 80 D) 20
Punkty 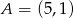 oraz
oraz 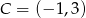 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 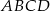 . Bok tego kwadratu ma długość:
. Bok tego kwadratu ma długość:
A) 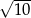 B)
B) 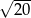 C)
C) 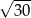 D)
D) 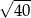
Punkty 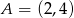 oraz
oraz 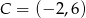 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 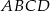 . Bok tego kwadratu ma długość:
. Bok tego kwadratu ma długość:
A) 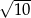 B)
B) 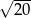 C)
C) 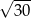 D)
D) 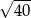
Punkty 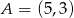 oraz
oraz 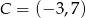 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 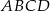 . Bok tego kwadratu ma długość:
. Bok tego kwadratu ma długość:
A) 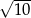 B)
B) 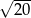 C)
C) 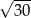 D)
D) 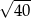
Punkt 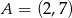 jest wierzchołkiem kwadratu
jest wierzchołkiem kwadratu 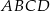 , a punkt
, a punkt 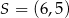 jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
A) 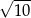 B)
B) 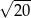 C)
C) 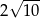 D)
D) 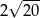
Punkt 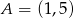 jest wierzchołkiem kwadratu
jest wierzchołkiem kwadratu 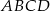 , a punkt
, a punkt 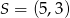 jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
jest środkiem okręgu opisanego na tym kwadracie. Bok tego kwadratu ma długość
A) 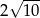 B)
B) 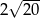 C)
C) 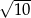 D)
D) 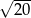
Przekątne deltoidu są zawarte w prostych o równaniach 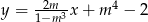 oraz
oraz 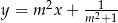 . Zatem
. Zatem
A) 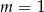 B)
B) 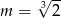 C)
C) 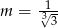 D)
D) 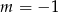
Jeżeli punkty 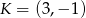 i
i 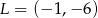 są środkami nierównoległych boków prostokąta, to długość przekątnej tego prostokąta jest równa
są środkami nierównoległych boków prostokąta, to długość przekątnej tego prostokąta jest równa
A) 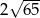 B)
B) 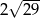 C)
C) 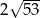 D)
D) 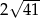
Punkty 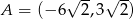 i
i 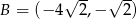 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 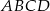 , którego przekątne przecinają się w punkcie
, którego przekątne przecinają się w punkcie 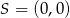 . Środek boku
. Środek boku 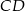 tego równoległoboku ma współrzędne
tego równoległoboku ma współrzędne
A) 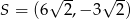 B)
B) 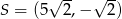 C)
C) 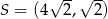 D)
D) 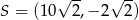
Punkty 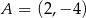 i
i 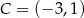 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 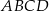 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 50 B) 100 C) 25 D) 12,5
Punkty 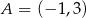 i
i 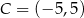 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 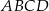 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 10 B) 25 C) 50 D) 100
W kartezjańskim układzie współrzędnych 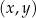 punkty
punkty 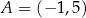 oraz
oraz 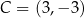 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 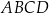 . Pole kwadratu
. Pole kwadratu 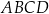 jest równe
jest równe
A) 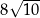 B)
B) 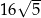 C) 40 D) 80
C) 40 D) 80
Punkty 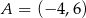 i
i 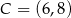 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 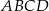 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 4 B) 52 C) 104 D) 26
Punkty 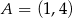 i
i 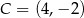 wyznaczają przekątną kwadratu
wyznaczają przekątną kwadratu 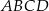 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 45 B) 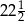 C) 18 D)
C) 18 D) 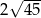
Punkty 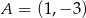 i
i 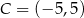 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 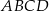 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 10 B) 25 C) 50 D) 100
W kartezjańskim układzie współrzędnych 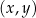 punkty
punkty 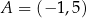 oraz
oraz 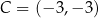 są wierzchołkami kwadratu
są wierzchołkami kwadratu 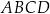 . Pole kwadratu
. Pole kwadratu 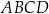 jest równe
jest równe
A) 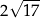 B)
B) 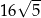 C) 68 D) 34
C) 68 D) 34
Punkty 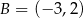 i
i 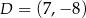 są przeciwległymi wierzchołkami kwadratu
są przeciwległymi wierzchołkami kwadratu 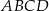 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 50 B) 100 C) 25 D) 200
Dłuższy z boków prostokąta 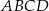 ma długość równą 12, a dwa sąsiednie wierzchołki mają współrzędne
ma długość równą 12, a dwa sąsiednie wierzchołki mają współrzędne 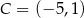 ,
, 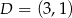 . Pole powierzchni tego prostokąta jest równe
. Pole powierzchni tego prostokąta jest równe
A) 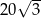 B) 64 C) 80 D) 96
B) 64 C) 80 D) 96
W prostokącie 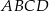 dane są wierzchołki
dane są wierzchołki 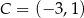 oraz
oraz 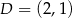 . Bok
. Bok 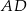 ma długość 6. Pole tego prostokąta jest równe
ma długość 6. Pole tego prostokąta jest równe
A) 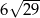 B)
B) 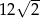 C) 24 D) 30
C) 24 D) 30
Punkty o współrzędnych: 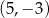 ,
, 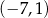 ,
, 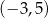 i
i 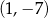 są wierzchołkami prostokąta. Pole tego prostokąta jest równe
są wierzchołkami prostokąta. Pole tego prostokąta jest równe
A) 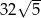 B) 32 C) 64 D)
B) 32 C) 64 D) 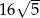
Punkty 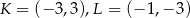 i
i 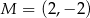 są środkami trzech kolejnych boków rombu. Pole tego rombu jest równe
są środkami trzech kolejnych boków rombu. Pole tego rombu jest równe
A) 80 B) 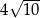 C) 40 D) 20
C) 40 D) 20
Dane są punkty o współrzędnych 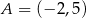 oraz
oraz 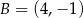 . Średnica okręgu wpisanego w kwadrat o boku
. Średnica okręgu wpisanego w kwadrat o boku 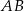 jest równa
jest równa
A) 12 B) 6 C) 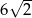 D)
D) 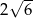
Dane są punkty o współrzędnych 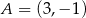 oraz
oraz 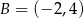 . Średnica okręgu wpisanego w kwadrat o boku
. Średnica okręgu wpisanego w kwadrat o boku 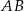 jest równa
jest równa
A) 10 B) 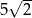 C) 5 D)
C) 5 D) 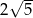
Punkty 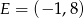 i
i 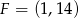 to środki boków, odpowiednio
to środki boków, odpowiednio 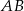 i
i 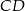 kwadratu
kwadratu 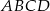 . Przekątna tego kwadratu ma długość
. Przekątna tego kwadratu ma długość
A) 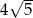 B) 10 C)
B) 10 C) 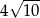 D) 20
D) 20
Punkty 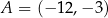 ,
, 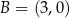 i
i 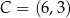 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 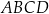 . Wierzchołek
. Wierzchołek 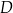 tego równoległoboku ma współrzędne
tego równoległoboku ma współrzędne
A) 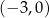 B)
B) 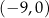 C)
C) 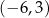 D)
D) 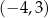
W kartezjańskim układzie współrzędnych 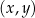 punkty
punkty 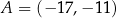 i
i 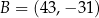 są wierzchołkami równoległoboku
są wierzchołkami równoległoboku 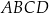 . Punkt
. Punkt 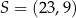 jest środkiem symetrii tego równoległoboku. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
jest środkiem symetrii tego równoległoboku. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Równoległobok 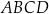 jest rombem. jest rombem. | P | F |
Równoległobok 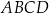 jest prostokątem. jest prostokątem. | P | F |
Punkty 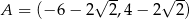 ,
, 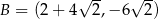 ,
, 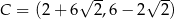 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 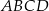 . Przekątne tego równoległoboku przecinają się w punkcie
. Przekątne tego równoległoboku przecinają się w punkcie
A) 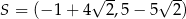 B)
B) 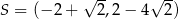
C) 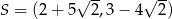 D)
D) 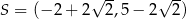
Punkty 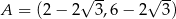 ,
, 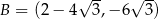 ,
, 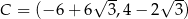 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 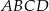 . Przekątne tego równoległoboku przecinają się w punkcie
. Przekątne tego równoległoboku przecinają się w punkcie
A) 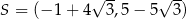 B)
B) 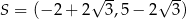
C) 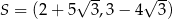 D)
D) 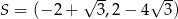
Punkty 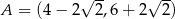 ,
, 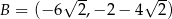 ,
, 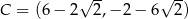 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 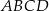 . Przekątne tego równoległoboku przecinają się w punkcie
. Przekątne tego równoległoboku przecinają się w punkcie
A) 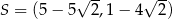 B)
B) 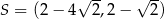
C) 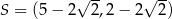 D)
D) 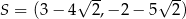
Dane są punkty o współrzędnych 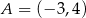 oraz
oraz 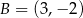 . Średnica okręgu opisanego na kwadracie o boku
. Średnica okręgu opisanego na kwadracie o boku 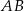 jest równa
jest równa
A) 12 B) 6 C) 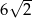 D)
D) 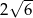
Punkty 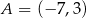 i
i 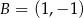 są sąsiednimi wierzchołkami kwadratu
są sąsiednimi wierzchołkami kwadratu 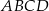 . Odcinek łączący środki dwóch sąsiednich boków tego kwadratu ma długość
. Odcinek łączący środki dwóch sąsiednich boków tego kwadratu ma długość
A) 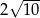 B)
B) 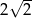 C)
C) 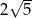 D)
D) 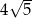
Przekątne rombu 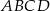 przecinają się w punkcie
przecinają się w punkcie 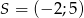 . Przekątna
. Przekątna 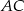 zawarta jest w prostej o równaniu
zawarta jest w prostej o równaniu 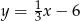 . Wskaż równanie prostej zawierającej przekątną
. Wskaż równanie prostej zawierającej przekątną 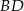 tego rombu.
tego rombu.
A) 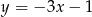 B)
B) 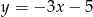 C)
C) 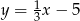 D)
D)