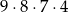Dany jest nieskończony ciąg geometryczny, w którym iloraz jest trzy razy większy od pierwszego wyrazu, a suma wszystkich wyrazów tego ciągu jest równa  . Pierwszy wyraz tego ciągu jest równy
. Pierwszy wyraz tego ciągu jest równy
A)  B)
B)  C)
C)  D) 7
D) 7
/Szkoła średnia
Funkcja liniowa 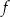 jest określona wzorem
jest określona wzorem 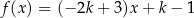 , gdzie
, gdzie 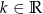 . Funkcja
. Funkcja 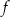 jest malejąca dla każdej liczby
jest malejąca dla każdej liczby 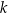 należącej do przedziału
należącej do przedziału
A) 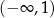 B)
B) 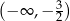 C)
C) 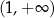 D)
D) 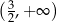
W urnie znajdują się jedynie kule białe i czarne. Kul białych jest trzy razy więcej niż czarnych. Oblicz, ile jest kul w urnie, jeśli przy jednoczesnym losowaniu dwóch kul prawdopodobieństwo otrzymania kul o różnych kolorach jest większe od 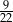 .
.
Ciąg 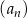 jest określony wzorem
jest określony wzorem 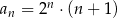 dla każdej liczby naturalnej
dla każdej liczby naturalnej 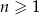 . Wyraz
. Wyraz 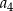 jest równy
jest równy
A) 64 B) 40 C) 48 D) 80
Dla każdej liczby rzeczywistej  różnej od
różnej od 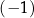 , 0 i 1, wartość wyrażenia
, 0 i 1, wartość wyrażenia 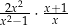 jest równa wartości wyrażenia
jest równa wartości wyrażenia
A) 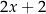 B)
B) 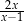 C)
C) 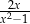 D)
D) 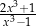
Prosta 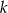 ma równanie
ma równanie 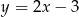 . Wskaż równanie prostej
. Wskaż równanie prostej 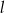 równoległej do prostej
równoległej do prostej 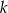 i przechodzącej przez punkt
i przechodzącej przez punkt 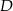 o współrzędnych
o współrzędnych 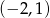 .
.
A) 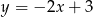 B)
B) 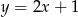 C)
C) 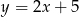 D)
D) 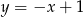
Ciąg 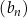 jest określony wzorem
jest określony wzorem 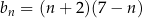 dla każdej liczby naturalnej
dla każdej liczby naturalnej 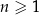 . Liczba dodatnich wyrazów ciągu
. Liczba dodatnich wyrazów ciągu 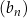 jest równa
jest równa
A) 6 B) 7 C) 8 D) 9
W trójkącie prostokątnym stosunek różnicy długości przyprostokątnych do długości przeciwprostokątnej jest równy 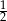 . Oblicz cosinusy kątów ostrych tego trójkąta.
. Oblicz cosinusy kątów ostrych tego trójkąta.
Prosta o równaniu 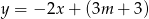 przecina w układzie współrzędnych oś
przecina w układzie współrzędnych oś 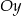 w punkcie
w punkcie 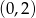 . Wtedy
. Wtedy
A) 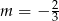 B)
B) 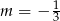 C)
C) 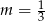 D)
D) 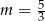
Na rysunku, w kartezjańskim układzie współrzędnych 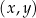 , przedstawiono dwie proste równoległe, które są interpretacją geometryczną jednego z poniższych układów równań.
, przedstawiono dwie proste równoległe, które są interpretacją geometryczną jednego z poniższych układów równań.
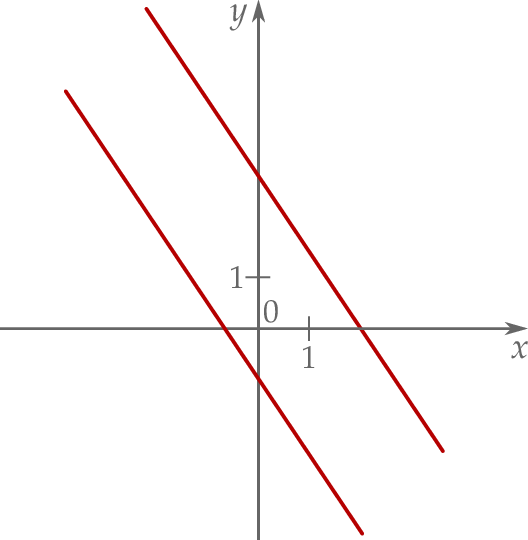
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 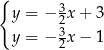 B)
B) 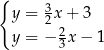
C) 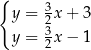 D)
D) 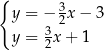
Do zbioru rozwiązań nierówności 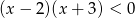 należy liczba
należy liczba
A) 9 B) 7 C) 4 D) 1
Dany jest rosnący ciąg geometryczny 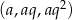 , którego wszystkie wyrazy i iloraz są liczbami całkowitymi nieparzystymi. Jeśli największy wyraz ciągu zmniejszymy o 4, to otrzymamy ciąg arytmetyczny. Oblicz wyraz
, którego wszystkie wyrazy i iloraz są liczbami całkowitymi nieparzystymi. Jeśli największy wyraz ciągu zmniejszymy o 4, to otrzymamy ciąg arytmetyczny. Oblicz wyraz 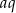 tego ciągu.
tego ciągu.
Na początku miesiąca komputer kosztował 3 500 zł. W drugiej dekadzie tego miesiąca cenę komputera obniżono o 10%, a w trzeciej dekadzie cena tego komputera została jeszcze raz obniżona, tym razem o 15%. Innych zmian ceny tego komputera w tym miesiącu już nie było. Cena komputera na koniec miesiąca była równa
A) 3 272,50 zł B) 2 625 zł C) 2 677,50 zł D) 2 800 zł
Wyznacz wszystkie wartości parametru 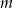 , dla których równanie
, dla których równanie
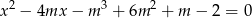
ma dwa różne pierwiastki rzeczywiste 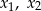 takie, że
takie, że 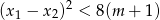 .
.
Pudełko w kształcie prostopadłościanu ma wymiary 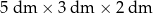 (zobacz rysunek).
(zobacz rysunek).
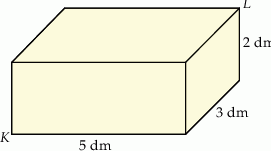
Przekątna 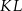 tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
A) 5,83 dm B) 6,16 dm C) 3,61 dm D) 5,39 dm
Właściciel sklepu z zabawkami przeprowadził lokalne badanie rynkowe dotyczące wpływu zmiany ceny zestawu klocków na liczbę kupujących ten produkt. Z badania wynika, że dzienny przychód 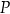 ze sprzedaży zestawów klocków, w zależności od kwoty obniżki ceny zestawu o
ze sprzedaży zestawów klocków, w zależności od kwoty obniżki ceny zestawu o  zł, wyraża się wzorem
zł, wyraża się wzorem
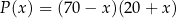
gdzie  jest liczbą całkowitą spełniającą warunki
jest liczbą całkowitą spełniającą warunki 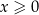 i
i 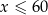 . Dzienny przychód ze sprzedaży zestawów klocków będzie równy 800 zł, gdy liczba
. Dzienny przychód ze sprzedaży zestawów klocków będzie równy 800 zł, gdy liczba  jest równa
jest równa
A) 25 B) 30 C) 45 D) 50 E) 60
Wykresem funkcji kwadratowej 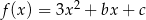 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie 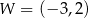 . Wzór tej funkcji w postaci kanonicznej to
. Wzór tej funkcji w postaci kanonicznej to
A) 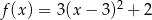 B)
B) 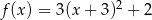
C) 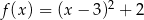 D)
D) 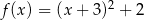
Dane są punkty 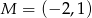 i
i 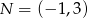 . Punkt
. Punkt 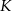 jest środkiem odcinka
jest środkiem odcinka 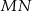 . Obrazem punktu
. Obrazem punktu 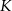 w symetrii względem początku układu współrzędnych jest punkt
w symetrii względem początku układu współrzędnych jest punkt
A) 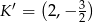 B)
B) 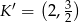 C)
C) 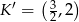 D)
D) 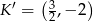
Liczba 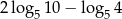 jest równa
jest równa
A) 2 B) 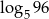 C)
C) 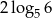 D) 5
D) 5
Liczba wszystkich dodatnich liczb czterocyfrowych parzystych, w których zapisie nie występują cyfry 0 i 2, jest równa
A) 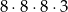 B)
B) 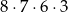 C)
C) 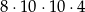 D)
D)