W trójkącie 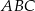 , w którym
, w którym 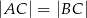 , na boku
, na boku 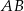 wybrano punkt
wybrano punkt 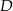 taki, że
taki, że 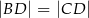 oraz
oraz 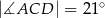 (zobacz rysunek).
(zobacz rysunek).
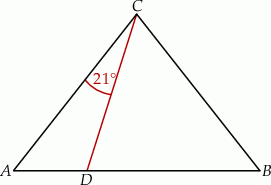
Wynika stąd, że kąt 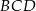 ma miarę
ma miarę
A) 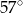 B)
B) 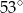 C)
C) 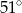 D)
D) 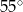
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trójkącie 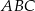 , w którym
, w którym 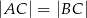 , na boku
, na boku 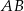 wybrano punkt
wybrano punkt 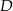 taki, że
taki, że 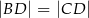 oraz
oraz 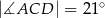 (zobacz rysunek).
(zobacz rysunek).

Wynika stąd, że kąt 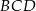 ma miarę
ma miarę
A) 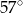 B)
B) 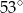 C)
C) 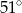 D)
D) 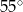
Dany jest ciąg 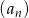 określony wzorem
określony wzorem 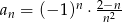 dla
dla 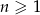 . Wówczas wyraz
. Wówczas wyraz 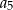 tego ciągu jest równy
tego ciągu jest równy
A) 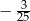 B)
B) 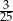 C)
C) 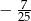 D)
D) 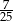
Ze zbioru liczb 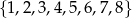 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 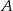 , polegającego na wylosowaniu liczb, z których pierwsza jest większa od drugiej o 4 lub 6.
, polegającego na wylosowaniu liczb, z których pierwsza jest większa od drugiej o 4 lub 6.
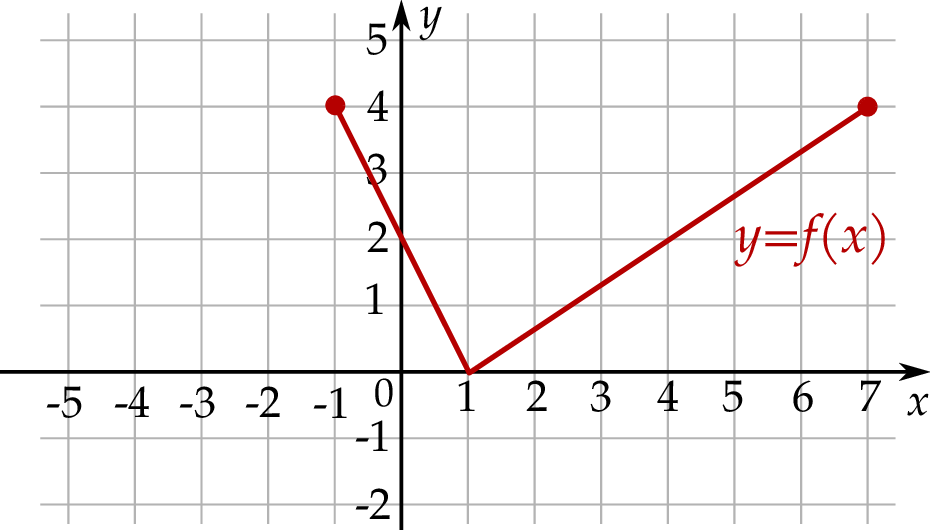
Na rysunku, w kartezjańskim układzie współrzędnych 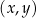 , przedstawiono wykres funkcji
, przedstawiono wykres funkcji 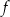 . Każdy z punktów przecięcia wykresu funkcji
. Każdy z punktów przecięcia wykresu funkcji 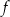 z prostą o równaniu
z prostą o równaniu 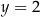 ma obie współrzędne całkowite.
ma obie współrzędne całkowite.
Wyznacz zbiór rozwiązań nierówności 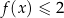 .
.
Wykaż, że liczba 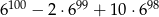 jest podzielna przez 17.
jest podzielna przez 17.
Dany jest trójkąt równoboczny 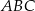 o boku długości 24. Punkt
o boku długości 24. Punkt 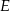 leży na boku
leży na boku 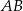 , a punkt
, a punkt 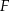 – na boku
– na boku 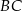 tego trójkąta. Odcinek
tego trójkąta. Odcinek 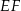 jest równoległy do boku
jest równoległy do boku 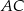 i przechodzi przez środek
i przechodzi przez środek 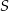 wysokości
wysokości 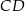 trójkąta
trójkąta  (zobacz rysunek).
(zobacz rysunek).
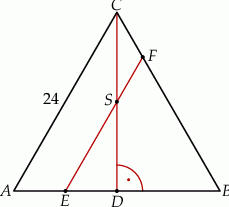
Oblicz długość odcinka 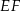 .
.
Sześciowyrazowy ciąg liczbowy 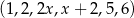 jest niemalejący. Mediana wyrazów tego ciągu jest równa 4. Wynika stąd, że
jest niemalejący. Mediana wyrazów tego ciągu jest równa 4. Wynika stąd, że
A) 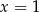 B)
B) 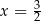 C)
C) 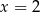 D)
D) 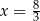
Udowodnij, że dla dowolnych liczb dodatnich 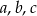 i
i 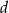 prawdziwa jest nierówność
prawdziwa jest nierówność
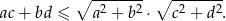
Rozwiązaniem układu równań 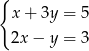 jest
jest
A) 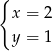 B)
B) 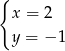 C)
C) 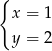 D)
D) 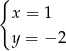
W kartezjańskim układzie współrzędnych 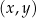 środek
środek 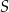 okręgu o promieniu
okręgu o promieniu 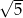 leży na prostej o równaniu
leży na prostej o równaniu 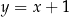 . Przez punkt
. Przez punkt 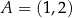 , którego odległość od punktu
, którego odległość od punktu 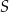 jest większa od
jest większa od 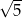 , poprowadzono dwie proste styczne do tego okręgu w punktach – odpowiednio –
, poprowadzono dwie proste styczne do tego okręgu w punktach – odpowiednio – 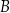 i
i 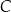 . Pole czworokąta
. Pole czworokąta 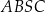 jest równe 15. Oblicz współrzędne punktu
jest równe 15. Oblicz współrzędne punktu 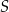 . Rozważ wszystkie przypadki.
. Rozważ wszystkie przypadki.
Wykaż, że dla każdej liczby naturalnej 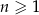 liczba
liczba 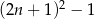 jest podzielna przez 8.
jest podzielna przez 8.
Punkty 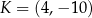 i
i 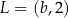 są końcami odcinka
są końcami odcinka 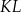 . Pierwsza współrzędna środka odcinka
. Pierwsza współrzędna środka odcinka 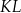 jest równa
jest równa 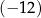 . Wynika stąd, że
. Wynika stąd, że
A) 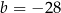 B)
B) 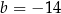 C)
C) 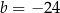 D)
D) 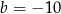
Rozwiąż nierówność 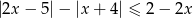 .
.
