Na rysunku 1 przedstawiony jest wykres funkcji 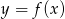 określonej dla
określonej dla 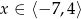 .
.
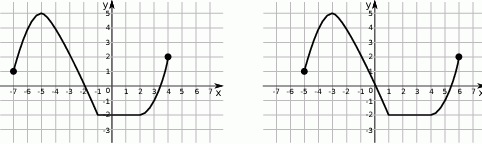
Rysunek 2 przedstawia wykres funkcji
A) 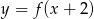 B)
B) 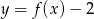 C)
C) 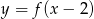 D)
D) 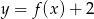
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku 1 przedstawiony jest wykres funkcji 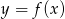 określonej dla
określonej dla 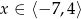 .
.

Rysunek 2 przedstawia wykres funkcji
A) 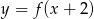 B)
B) 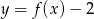 C)
C) 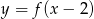 D)
D) 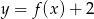
W kartezjańskim układzie współrzędnych 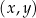 dane są punkty
dane są punkty 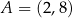 oraz
oraz 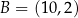 . Symetralna odcinka
. Symetralna odcinka 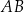 przecina oś
przecina oś 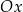 układu współrzędnych w punkcie
układu współrzędnych w punkcie 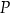 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 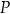 oraz długość odcinka
oraz długość odcinka 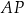 .
.
Ze zbioru pięciu liczb 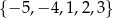 losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie
losujemy kolejno ze zwracaniem dwa razy po jednej liczbie. Zdarzenie 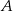 polega na wylosowaniu dwóch liczb, których iloczyn jest ujemny. Oblicz prawdopodobieństwo zdarzenia
polega na wylosowaniu dwóch liczb, których iloczyn jest ujemny. Oblicz prawdopodobieństwo zdarzenia 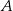 .
.
Liczba 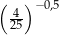 jest równa
jest równa
A) 0,04 B) 0,8 C) 2,5 D) 0,4
Wykaż, że dla każdej liczby naturalnej 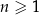 liczba
liczba 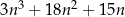 jest podzielna przez 6.
jest podzielna przez 6.
Liczba przekątnych wielokąta wypukłego, w którym jest  boków i
boków i 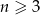 wyraża się wzorem
wyraża się wzorem 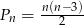 .
.
Suma 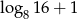 jest równa
jest równa
A) 3 B)  C)
C) 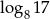 D)
D) 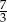
Ciąg 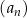 jest określony wzorem
jest określony wzorem 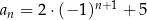 dla każdej liczby naturalnej
dla każdej liczby naturalnej 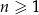 . Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
A) 3 B) 7 C) 50 D) 100
Wykaż, że dla każdej liczby naturalnej 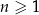 liczba
liczba 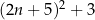 jest podzielna przez 4.
jest podzielna przez 4.
Proste o równaniach: 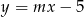 i
i 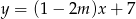 są równoległe, gdy
są równoległe, gdy
A) 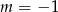 B)
B) 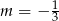 C)
C) 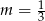 D)
D) 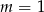
Medianą zestawu danych 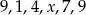 jest liczba 8. Wtedy
jest liczba 8. Wtedy  może być równe
może być równe
A) 8 B) 4 C) 7 D) 9
Punkty 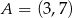 i
i 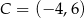 są końcami przekątnej kwadratu
są końcami przekątnej kwadratu 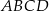 . Promień okręgu opisanego na tym kwadracie jest równy
. Promień okręgu opisanego na tym kwadracie jest równy
A) 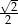 B)
B)  C)
C) 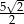 D) 5
D) 5
Rozwiąż równanie 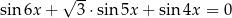 .
.
Liczba 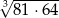 jest równa
jest równa
A) 72 B) 36 C) 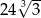 D)
D) 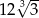
Dziewiąty wyraz ciągu arytmetycznego 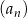 , określonego dla
, określonego dla 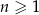 , jest równy 34, a suma jego ośmiu początkowych wyrazów jest równa 110. Oblicz pierwszy wyraz i różnicę tego ciągu.
, jest równy 34, a suma jego ośmiu początkowych wyrazów jest równa 110. Oblicz pierwszy wyraz i różnicę tego ciągu.
Miara kąta wpisanego w okrąg jest o 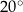 mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa
mniejsza od miary kąta środkowego opartego na tym samym łuku. Wynika stąd, że miara kąta wpisanego jest równa
A) 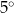 B)
B) 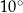 C)
C) 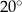 D)
D) 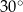
Flagę, taką jak pokazano na rysunku, należy zszyć z trzech jednakowej szerokości pasów kolorowej tkaniny. Oba pasy zewnętrzne mają być tego samego koloru, a pas znajdujący się między nimi ma być innego koloru. Liczba różnych takich flag, które można uszyć, mając do dyspozycji tkaniny w 10 kolorach, jest równa

A) 100 B) 99 C) 90 D) 19
Ciąg 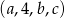 jest arytmetyczny, a ciąg
jest arytmetyczny, a ciąg 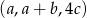 jest geometryczny. Oblicz
jest geometryczny. Oblicz 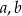 i
i  .
.
Dany jest sześcian 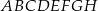 . Sinus kąta
. Sinus kąta  nachylenia przekątnej
nachylenia przekątnej 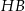 tego sześcianu do płaszczyzny podstawy
tego sześcianu do płaszczyzny podstawy 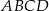 (zobacz rysunek) jest równy
(zobacz rysunek) jest równy
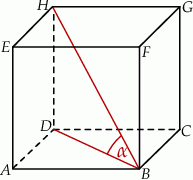
A) 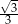 B)
B) 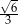 C)
C) 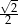 D)
D) 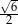
Punkty 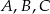 i
i 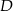 leżą na okręgu o środku
leżą na okręgu o środku 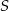 . Cięciwa
. Cięciwa 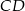 przecina średnicę
przecina średnicę 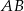 tego okręgu w punkcie
tego okręgu w punkcie 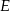 tak, że
tak, że 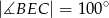 . Kąt środkowy
. Kąt środkowy 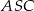 ma miarę
ma miarę 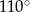 (zobacz rysunek).
(zobacz rysunek).
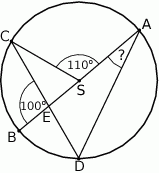
Kąt wpisany 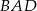 ma miarę
ma miarę
A) 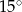 B)
B) 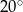 C)
C) 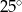 D)
D)