Podstawą ostrosłupa prawidłowego 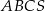 jest trójkąt równoboczny
jest trójkąt równoboczny 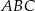 o boku długości 6. Na krawędziach bocznych
o boku długości 6. Na krawędziach bocznych 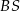 i
i 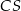 wybrano punkty, odpowiednio
wybrano punkty, odpowiednio 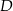 i
i 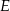 , takie że
, takie że 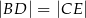 oraz
oraz 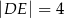 (zobacz rysunek). Płaszczyzna
(zobacz rysunek). Płaszczyzna 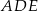 jest prostopadła do płaszczyzny ściany bocznej
jest prostopadła do płaszczyzny ściany bocznej 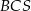 ostrosłupa.
ostrosłupa.
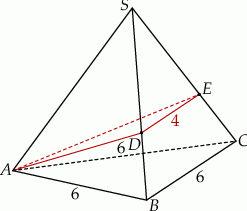
Oblicz objętość tego ostrosłupa.

 określony wzorem
określony wzorem 
 i z dzielenia przez
i z dzielenia przez  daje resztę równą 6.
daje resztę równą 6.  i z dzielenia przez
i z dzielenia przez 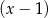 daje resztę równą 6.
daje resztę równą 6. 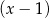 i jest podzielny przez
i jest podzielny przez 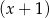 .
. 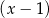 , ani przez
, ani przez 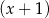 .
. 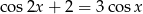 .
. 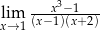 jest równa
jest równa 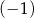
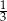
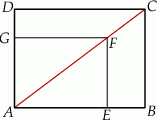
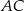 prostokąta
prostokąta 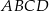 ma długość 70. Na boku
ma długość 70. Na boku 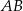 obrano punkt
obrano punkt 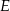 , na przekątnej
, na przekątnej 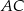 obrano punkt
obrano punkt 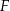 , a na boku
, a na boku 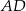 obrano punkt
obrano punkt 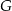 – tak, że czworokąt
– tak, że czworokąt 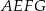 jest prostokątem (zobacz rysunek). Ponadto
jest prostokątem (zobacz rysunek). Ponadto 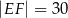 i
i 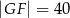 .
. 
 jest równy
jest równy  dla
dla  jest równa
jest równa 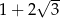
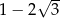
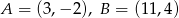 . Na prostej o równaniu
. Na prostej o równaniu 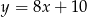 znajdź punkt
znajdź punkt 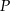 , dla którego suma
, dla którego suma 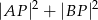 jest najmniejsza.
jest najmniejsza. 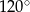 jest równe
jest równe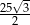
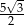
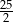
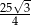
 prawdziwa jest tożsamość
prawdziwa jest tożsamość 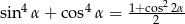 .
. 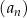 jest określony wzorem
jest określony wzorem 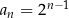 , dla każdej liczby naturalnej
, dla każdej liczby naturalnej 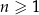 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy 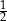
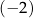
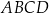 , w którym przekątna
, w którym przekątna 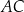 jest prostopadła do ramienia
jest prostopadła do ramienia 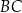 ,
, 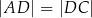 oraz
oraz 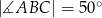 (zobacz rysunek).
(zobacz rysunek). 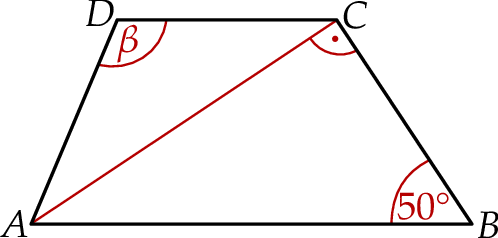
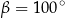
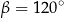
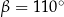
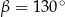
 ma długość
ma długość 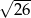 . Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2:3. Oblicz pole tego trapezu.
. Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2:3. Oblicz pole tego trapezu. 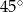 . Wysokość tego stożka jest równa
. Wysokość tego stożka jest równa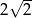
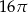
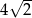
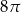
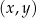 dany jest okrąg
dany jest okrąg 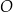 o środku
o środku 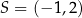 i promieniu 3. Okrąg
i promieniu 3. Okrąg 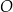 jest określony równaniem
jest określony równaniem 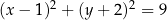
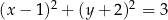
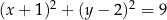
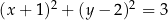
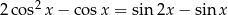 w przedziale
w przedziale 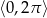 .
. 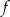 określona wzorem
określona wzorem 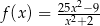 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Oblicz wartość
. Oblicz wartość 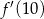 pochodnej tej funkcji dla argumentu 10.
pochodnej tej funkcji dla argumentu 10. 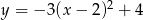 jest punkt o współrzędnych
jest punkt o współrzędnych 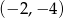
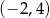
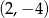
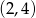
 , jest równa
, jest równa 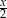 . Mediana tych liczb jest równa
. Mediana tych liczb jest równa 