Wynikiem działania 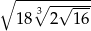 jest
jest
A) 36 B) 16 C) 12 D) 6
/Szkoła średnia
Liczba 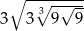 jest równa
jest równa
A) 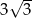 B)
B) 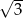 C) 3 D) 9
C) 3 D) 9
Wynikiem działania 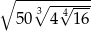 jest
jest
A) 100 B) 20 C) 10 D) 15
Liczba 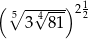 jest równa
jest równa
A) 3 B) 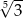 C)
C) 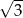 D) 9
D) 9
Prostokąt 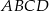 obracając się wokół boku
obracając się wokół boku 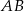 , zakreślił walec
, zakreślił walec 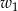 . Ten sam prostokąt obracając się wokół boku
. Ten sam prostokąt obracając się wokół boku 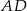 , zakreślił walec
, zakreślił walec 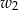 . Otrzymane walce mają równe pola powierzchni całkowitych. Wykaż, że prostokąt
. Otrzymane walce mają równe pola powierzchni całkowitych. Wykaż, że prostokąt 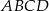 jest kwadratem.
jest kwadratem.
Wyrażenie 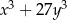 jest równe iloczynowi
jest równe iloczynowi
A) 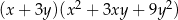 B)
B) 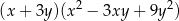
C) 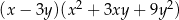 D)
D) 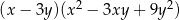
Wyrażenie 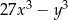 jest równe iloczynowi
jest równe iloczynowi
A) 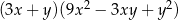 B)
B) 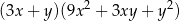
C) 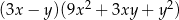 D)
D) 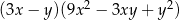
Wyrażenie 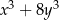 jest równe iloczynowi
jest równe iloczynowi
A) 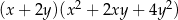 B)
B) 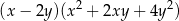
C) 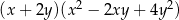 D)
D) 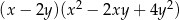
Wyrażenie 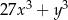 jest równe iloczynowi
jest równe iloczynowi
A) 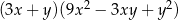 B)
B) 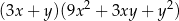
C) 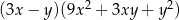 D)
D) 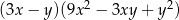
Zdarzenia losowe 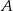 i
i 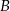 są zawarte w przestrzeni
są zawarte w przestrzeni 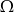 . Wiedząc, że
. Wiedząc, że 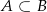 oraz
oraz 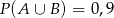 , oblicz
, oblicz 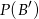 .
.
Wysokość podstawy graniastosłupa prawidłowego trójkątnego ma długość 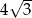 , zaś przekątna ściany bocznej tworzy z krawędzią podstawy kąt równy
, zaś przekątna ściany bocznej tworzy z krawędzią podstawy kąt równy 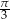 . Graniastosłup ten wpisano w walec. Oblicz pole powierzchni i objętość walca.
. Graniastosłup ten wpisano w walec. Oblicz pole powierzchni i objętość walca.
Na seans filmowy sprzedano 280 biletów, w tym 126 ulgowych. Jaki procent sprzedanych biletów stanowiły bilety ulgowe?
A) 22% B) 33% C) 45% D) 63%
Na seans filmowy sprzedano 420 biletów, w tym 189 ulgowych. Jaki procent sprzedanych biletów stanowiły bilety ulgowe?
A) 63% B) 45% C) 33% D) 22%
Na seans filmowy sprzedano 280 biletów, w tym 84 ulgowych. Jaki procent sprzedanych biletów stanowiły bilety ulgowe?
A) 14% B) 22% C) 30% D) 42%
Na koncert sprzedano 680 biletów, w tym 306 na miejsca siedzące. Jaki procent sprzedanych biletów stanowiły bilety na miejsca siedzące?
A) 63% B) 45% C) 33% D) 22%
Funkcja 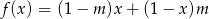 jest rosnąca, gdy
jest rosnąca, gdy
A) 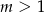 B)
B) 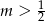 C)
C) 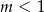 D)
D) 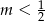
Mamy trzy pudełka: w pierwszym znajduje się 6 kul ponumerowanych kolejnymi liczbami od 1 do 6, w drugim – 4 kule ponumerowane kolejnymi liczbami od 1 do 4, a w trzecim – 5 kul ponumerowanych kolejnymi liczbami od 1 do 5. Losujemy po jednej kuli z każdego pudełka i tworzymy liczbę trzycyfrową w ten sposób, że numer kuli wylosowanej z pierwszego pudełka jest cyfrą setek, numer kuli wylosowanej z drugiego pudełka jest cyfrą dziesiątek, a numer kuli wylosowanej z trzeciego – cyfrą jedności tej liczby. Oblicz prawdopodobieństwo, że utworzona liczba jest podzielna przez 4.
Trzy liczby dodatnie 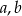 i
i  tworzą ciąg geometryczny. Suma tych liczb jest równa 26, a suma ich odwrotności wynosi
tworzą ciąg geometryczny. Suma tych liczb jest równa 26, a suma ich odwrotności wynosi 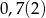 . Znajdź te liczby.
. Znajdź te liczby.
Punkty 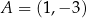 oraz
oraz 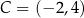 są końcami przekątnej
są końcami przekątnej 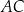 rombu
rombu 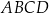 . Środek przekątnej
. Środek przekątnej 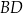 tego rombu ma współrzędne
tego rombu ma współrzędne
A) 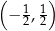 B)
B) 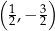 C)
C) 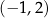 D)
D) 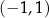
Klasy IIIa i IIIb liczą odpowiednio 10 dziewcząt i 18 chłopców oraz 16 dziewcząt i 12 chłopców. Wybieramy losowo jedną z tych dwóch klas i losujemy z niej jednego ucznia. Jakie jest prawdopodobieństwo wylosowania dziewczynki?
Rozwiąż algebraicznie układ równań 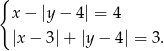
Wielkości  i
i 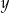 są odwrotnie proporcjonalne (tabela poniżej).
są odwrotnie proporcjonalne (tabela poniżej).
 |  | 3 | 8 |
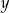 | 36 | 24 | 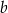 |
Stąd wynika, że
A) 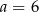 ,
, 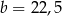 B)
B) 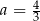 ,
, 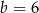 C)
C) 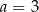 ,
, 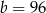 D)
D) 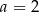 ,
, 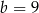
Wielkości  i
i 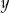 są odwrotnie proporcjonalne (tabela poniżej).
są odwrotnie proporcjonalne (tabela poniżej).
 | 3 |  | 2 |
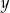 | 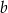 | 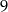 | 36 |
Stąd wynika, że
A) 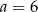 ,
, 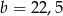 B)
B) 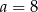 ,
, 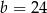 C)
C) 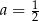 ,
, 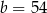 D)
D) 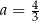 ,
, 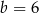
Znajdź równanie krzywej, którą tworzą wszystkie punkty jednakowo odległe od okręgu 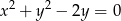 i od prostej
i od prostej 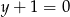 .
.
Z talii 52 kart losujemy dwa razy po jednej karcie (ze zwracaniem). Niech 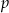 oznacza prawdopodobieństwo wylosowania dwóch królów. Wtedy
oznacza prawdopodobieństwo wylosowania dwóch królów. Wtedy
A) 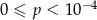 B)
B) 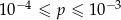 C)
C) 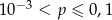 D)
D) 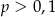
Dla jakich wartości parametru 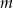 funkcja
funkcja 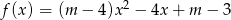 ma dwa miejsca zerowe, z których jedno jest mniejsze od 1, a drugie większe od 1?
ma dwa miejsca zerowe, z których jedno jest mniejsze od 1, a drugie większe od 1?
Dany jest trójmian kwadratowy 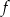 o współczynniku 2 przy najwyższej potędze
o współczynniku 2 przy najwyższej potędze  . Wierzchołek paraboli będącej wykresem tego trójmianu ma współrzędne
. Wierzchołek paraboli będącej wykresem tego trójmianu ma współrzędne 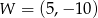 . Oblicz
. Oblicz 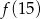 .
.
Reszta z dzielenia wielomianu 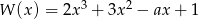 przez dwumian
przez dwumian 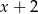 jest równa
jest równa 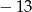 . Zatem
. Zatem
A) 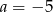 B)
B) 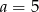 C)
C) 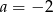 D)
D) 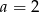
Reszta z dzielenia wielomianu 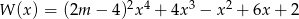 przez dwumian
przez dwumian 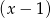 jest równa 11 dla
jest równa 11 dla
A) 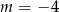 B)
B) 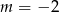 C)
C) 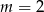 D)
D) 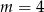
Reszta z dzielenia wielomianu 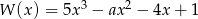 przez dwumian
przez dwumian 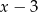 jest równa 88. Zatem
jest równa 88. Zatem
A) 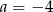 B)
B) 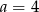 C)
C) 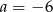 D)
D) 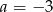
W pudełku zmieszano 30 ziaren fasoli, 20 ziaren ciecierzycy i 50 ziaren grochu.
- Losujemy jedno ziarenko. Jakie jest prawdopodobieństwo wylosowania ziarenka ciecierzycy?
- Jako pierwsze wylosowano ziarenko fasoli. Jakie jest prawdopodobieństwo, że drugim wylosowanym ziarenkiem nie będzie ziarenko fasoli?
- Z pudełka usunięto po 10% ziarenek każdego rodzaju. Jakie jest prawdopodobieństwo wylosowania ziarenka fasoli?
Ze zbioru liczb 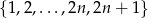 ,
, 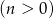 , losujemy jednocześnie dwie liczby. Niech
, losujemy jednocześnie dwie liczby. Niech 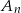 oznacza zdarzenie: iloczyn wylosowanych liczb będzie liczbą parzystą. Wyznacz prawdopodobieństwo tego zdarzenia.
oznacza zdarzenie: iloczyn wylosowanych liczb będzie liczbą parzystą. Wyznacz prawdopodobieństwo tego zdarzenia.

