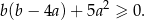Rozwiąż równanie
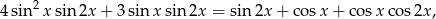
dla 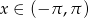 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie
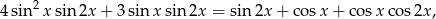
dla 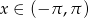 .
.
Wiadomo, że 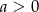 i
i 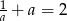 . Wykaż, że
. Wykaż, że 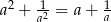 .
.
Uzasadnij, że jeżeli  jest liczbą rzeczywistą różną od zera i
jest liczbą rzeczywistą różną od zera i 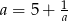 , to
, to 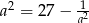 .
.
Uzasadnij, że jeżeli  jest liczbą rzeczywistą różną od zera i
jest liczbą rzeczywistą różną od zera i 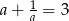 , to
, to 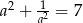 .
.
Uzasadnij, że jeżeli prostokąt 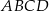 nie jest kwadratem, to punkty przecięcia dwusiecznych jego kątów wewnętrznych są wierzchołkami kwadratu.
nie jest kwadratem, to punkty przecięcia dwusiecznych jego kątów wewnętrznych są wierzchołkami kwadratu.

Narysuj wykres funkcji 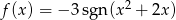 . Podaj zbiór wartości funkcji.
. Podaj zbiór wartości funkcji.
Rozwiąż układ równań 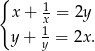
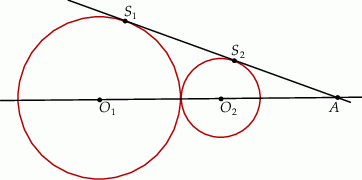
Dane są 2 koła styczne zewnętrznie o promieniach  i
i  (
(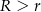 ) oraz środkach
) oraz środkach 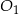 i
i 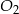 . Do tych kół poprowadzono wspólną styczną, która jest styczna do tych okręgów w punktach
. Do tych kół poprowadzono wspólną styczną, która jest styczna do tych okręgów w punktach 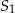 i
i 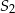 odpowiednio (
odpowiednio (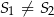 ). Oblicz pole trójkąta
). Oblicz pole trójkąta 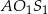 , gdzie
, gdzie 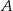 jest punktem przecięcia się prostych
jest punktem przecięcia się prostych 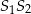 i
i 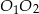 .
.
Dane są punkty 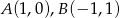 . Punkt
. Punkt 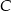 należy do okręgu o równaniu
należy do okręgu o równaniu 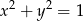 . Znajdź współrzędne punktu
. Znajdź współrzędne punktu 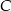 tak, aby pole trójkąta
tak, aby pole trójkąta 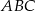 było największe. Oblicz to pole.
było największe. Oblicz to pole.
Dane są punkty 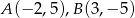 . Punkt
. Punkt 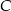 należy do okręgu o równaniu
należy do okręgu o równaniu 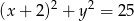 . Znajdź współrzędne punktu
. Znajdź współrzędne punktu 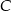 tak, aby pole trójkąta
tak, aby pole trójkąta 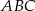 było największe. Oblicz to pole.
było największe. Oblicz to pole.
Wielomian 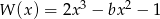 jest podzielny przez dwumian
jest podzielny przez dwumian 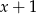 . Wynika stąd, że
. Wynika stąd, że
A) 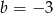 B)
B) 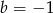 C)
C) 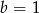 D)
D) 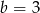
Wielomian 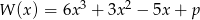 jest podzielny przez dwumian
jest podzielny przez dwumian 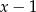 dla
dla 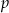 równego
równego
A) 4 B) 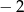 C) 2 D)
C) 2 D) 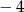
Wielomian 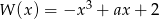 jest podzielny przez dwumian
jest podzielny przez dwumian 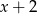 . Wynika stąd, że
. Wynika stąd, że
A) 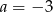 B)
B) 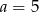 C)
C) 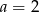 D)
D) 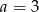
Wielomian 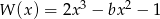 jest podzielny przez dwumian
jest podzielny przez dwumian 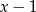 . Wynika stąd, że
. Wynika stąd, że
A) 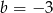 B)
B) 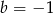 C)
C) 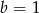 D)
D) 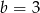
Oblicz sumę stu najmniejszych dodatnich rozwiązań równania 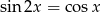 .
.
Wykaż, że dla dowolnego kąta ostrego  , wartość wyrażenia
, wartość wyrażenia 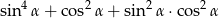 jest stała.
jest stała.
Wykaż, że dla dowolnego kąta  ,
,
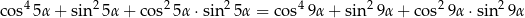
Wykaż, że dla dowolnego kąta ostrego  , wartość wyrażenia
, wartość wyrażenia 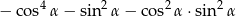 jest stała.
jest stała.
Dla kąta ostrego  spełniony jest warunek
spełniony jest warunek 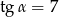 . Wówczas wartość wyrażenia
. Wówczas wartość wyrażenia 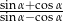 jest równa
jest równa
A) 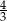 B)
B)  C)
C)  D)
D) 
Jeżeli  jest kątem ostrym oraz
jest kątem ostrym oraz 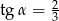 , to wartość wyrażenia
, to wartość wyrażenia 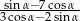 jest równa
jest równa
A) 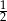 B)
B) 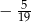 C)
C) 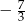 D)
D) 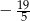
Jeżeli kąt  jest ostry i
jest ostry i 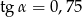 , to wartość wyrażenia
, to wartość wyrażenia 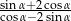 jest równa
jest równa
A) 11 B) 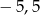 C)
C) 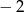 D)
D) 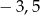
Jeżeli 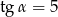 , to wartość wyrażenia
, to wartość wyrażenia 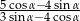 jest równa
jest równa
A) 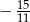 B)
B) 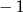 C)
C) 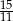 D)
D) 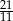
Jeżeli  jest kątem ostrym oraz
jest kątem ostrym oraz 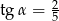 , to wartość wyrażenia
, to wartość wyrażenia 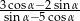 jest równa
jest równa
A) 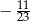 B)
B) 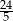 C)
C) 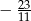 D)
D) 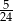
W okręgu o środku w punkcie 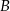 kąt środkowy
kąt środkowy  i kąt wpisany
i kąt wpisany 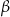 oparte są na tym samym łuku wyznaczonym przez punkty
oparte są na tym samym łuku wyznaczonym przez punkty 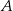 i
i 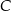 leżące na okręgu. Suma miar tych kątów jest równa kątowi prostemu. Wierzchołek kąta
leżące na okręgu. Suma miar tych kątów jest równa kątowi prostemu. Wierzchołek kąta 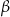 znajduje się w punkcie
znajduje się w punkcie 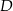 . Wynika stąd, że trójkąt
. Wynika stąd, że trójkąt
A) 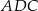 jest równoboczny B)
jest równoboczny B) 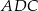 jest prostokątny
jest prostokątny
C) 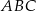 jest równoboczny D)
jest równoboczny D) 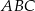 jest prostokątny
jest prostokątny
W okręgu o środku w punkcie 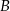 kąt środkowy
kąt środkowy  i kąt wpisany
i kąt wpisany 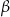 oparte są na tym samym łuku wyznaczonym przez punkty
oparte są na tym samym łuku wyznaczonym przez punkty 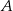 i
i 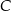 leżące na okręgu. Suma miar tych kątów jest równa
leżące na okręgu. Suma miar tych kątów jest równa 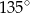 . Wierzchołek kąta
. Wierzchołek kąta 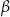 znajduje się w punkcie
znajduje się w punkcie 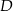 . Wynika stąd, że trójkąt
. Wynika stąd, że trójkąt
A) 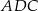 jest równoboczny B)
jest równoboczny B) 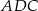 jest prostokątny
jest prostokątny
C) 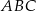 jest równoboczny D)
jest równoboczny D) 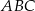 jest prostokątny
jest prostokątny
W okręgu o środku w punkcie 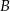 kąt środkowy
kąt środkowy  i kąt wpisany
i kąt wpisany 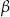 oparte są na tym samym łuku wyznaczonym przez punkty
oparte są na tym samym łuku wyznaczonym przez punkty 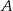 i
i 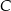 leżące na okręgu. Różnica miar tych kątów jest równa
leżące na okręgu. Różnica miar tych kątów jest równa 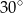 . Wierzchołek kąta
. Wierzchołek kąta 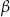 znajduje się w punkcie
znajduje się w punkcie 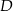 . Wynika stąd, że trójkąt
. Wynika stąd, że trójkąt
A) 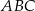 jest równoboczny B)
jest równoboczny B) 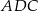 jest prostokątny
jest prostokątny
C) 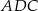 jest równoboczny D)
jest równoboczny D) 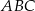 jest prostokątny
jest prostokątny
W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość 4, wysokość ostrosłupa ma długość 5. Ściana boczna jest nachylona do podstawy pod kątem  takim, że
takim, że
A) 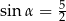 B)
B) 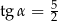 C)
C) 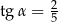 D)
D) 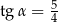
Podstawą ostrosłupa prawidłowego czworokątnego jest kwadrat o boku długości 4. Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod takim kątem  , że
, że 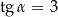 . Wysokość tego ostrosłupa jest równa
. Wysokość tego ostrosłupa jest równa
A) 3 B) 6 C) 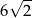 D) 12
D) 12
Rozwiąż równanie 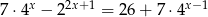 .
.
Średnia arytmetyczna ocen Jacka jest równa 3,75, a średnia ocen Karola (liczona z dokładnie tej samej liczby ocen) jest równa 4,25. Średnia ocen obu chłopców jest równa
A) 3,95 B) 4,5 C) 4,0 D) 4,15
Średnia arytmetyczna ocen Zosi jest równa 2,8, a średnia ocen Basi (liczona z dokładnie tej samej liczby ocen) jest równa 4,4. Średnia ocen obu dziewcząt jest równa
A) 3,6 B) 4,0 C) 3,8 D) 4,15
Spośród liczb dwucyfrowych wybrano bez zwracania dwa razy po jednej liczbie. Oblicz prawdopodobieństwo, że dwa razy wybrano liczbę parzystą.
Spośród dodatnich liczb dwucyfrowych losujemy kolejno bez zwracania dwie liczby. Oblicz prawdopodobieństwo wylosowania dwóch liczb parzystych.
Rozwiąż nierówność
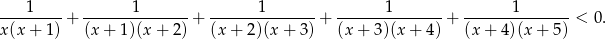
O zdarzeniach 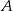 i
i 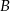 wiadomo, że
wiadomo, że 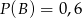 ,
, 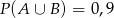 oraz
oraz 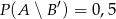 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 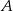 .
.
Podstawą ostrosłupa 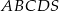 jest prostokąt
jest prostokąt 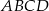 o bokach długości
o bokach długości 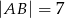 i
i 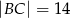 . Krawędź
. Krawędź 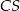 jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt
jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt 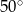 . Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość.
. Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość.
Uzasadnij, że nierówność 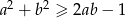 jest prawdziwa dla dowolnych liczb rzeczywistych
jest prawdziwa dla dowolnych liczb rzeczywistych  i
i 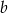 .
.
Wykaż, że dla każdej liczby rzeczywistej  różnej od 0 i każdej liczby rzeczywistej
różnej od 0 i każdej liczby rzeczywistej 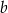 różnej od 0 spełniona jest nierówność
różnej od 0 spełniona jest nierówność
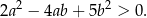
Wykaż, że dla każdych dwóch różnych liczb rzeczywistych  i
i 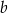 prawdziwa jest nierówność
prawdziwa jest nierówność
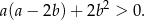
Wykaż, że dla każdych dwóch liczb rzeczywistych  i
i 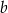 prawdziwa jest nierówność
prawdziwa jest nierówność