Dla kąta ostrego  spełniony jest warunek
spełniony jest warunek 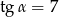 . Wówczas wartość wyrażenia
. Wówczas wartość wyrażenia 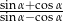 jest równa
jest równa
A) 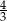 B)
B)  C)
C)  D)
D) 
/Szkoła średnia
Jeżeli 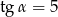 , to wartość wyrażenia
, to wartość wyrażenia 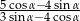 jest równa
jest równa
A) 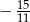 B)
B) 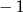 C)
C) 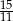 D)
D) 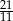
Jeżeli  jest kątem ostrym oraz
jest kątem ostrym oraz 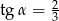 , to wartość wyrażenia
, to wartość wyrażenia 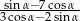 jest równa
jest równa
A) 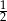 B)
B) 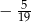 C)
C) 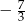 D)
D) 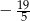
Jeżeli kąt  jest ostry i
jest ostry i 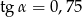 , to wartość wyrażenia
, to wartość wyrażenia 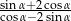 jest równa
jest równa
A) 11 B) 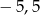 C)
C) 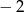 D)
D) 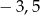
Jeżeli  jest kątem ostrym oraz
jest kątem ostrym oraz 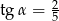 , to wartość wyrażenia
, to wartość wyrażenia 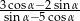 jest równa
jest równa
A) 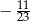 B)
B) 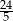 C)
C) 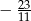 D)
D) 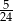
W okręgu o środku w punkcie 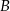 kąt środkowy
kąt środkowy  i kąt wpisany
i kąt wpisany 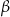 oparte są na tym samym łuku wyznaczonym przez punkty
oparte są na tym samym łuku wyznaczonym przez punkty 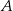 i
i 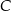 leżące na okręgu. Suma miar tych kątów jest równa kątowi prostemu. Wierzchołek kąta
leżące na okręgu. Suma miar tych kątów jest równa kątowi prostemu. Wierzchołek kąta 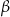 znajduje się w punkcie
znajduje się w punkcie 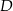 . Wynika stąd, że trójkąt
. Wynika stąd, że trójkąt
A) 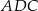 jest równoboczny B)
jest równoboczny B) 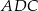 jest prostokątny
jest prostokątny
C) 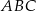 jest równoboczny D)
jest równoboczny D) 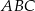 jest prostokątny
jest prostokątny
W okręgu o środku w punkcie 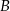 kąt środkowy
kąt środkowy  i kąt wpisany
i kąt wpisany 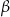 oparte są na tym samym łuku wyznaczonym przez punkty
oparte są na tym samym łuku wyznaczonym przez punkty 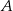 i
i 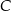 leżące na okręgu. Suma miar tych kątów jest równa
leżące na okręgu. Suma miar tych kątów jest równa 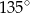 . Wierzchołek kąta
. Wierzchołek kąta 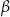 znajduje się w punkcie
znajduje się w punkcie 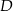 . Wynika stąd, że trójkąt
. Wynika stąd, że trójkąt
A) 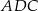 jest równoboczny B)
jest równoboczny B) 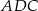 jest prostokątny
jest prostokątny
C) 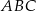 jest równoboczny D)
jest równoboczny D) 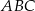 jest prostokątny
jest prostokątny
W okręgu o środku w punkcie 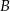 kąt środkowy
kąt środkowy  i kąt wpisany
i kąt wpisany 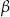 oparte są na tym samym łuku wyznaczonym przez punkty
oparte są na tym samym łuku wyznaczonym przez punkty 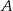 i
i 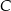 leżące na okręgu. Różnica miar tych kątów jest równa
leżące na okręgu. Różnica miar tych kątów jest równa 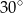 . Wierzchołek kąta
. Wierzchołek kąta 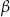 znajduje się w punkcie
znajduje się w punkcie 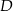 . Wynika stąd, że trójkąt
. Wynika stąd, że trójkąt
A) 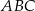 jest równoboczny B)
jest równoboczny B) 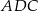 jest prostokątny
jest prostokątny
C) 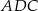 jest równoboczny D)
jest równoboczny D) 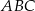 jest prostokątny
jest prostokątny
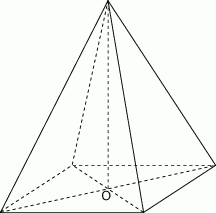
W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość 4, wysokość ostrosłupa ma długość 5. Ściana boczna jest nachylona do podstawy pod kątem  takim, że
takim, że
A) 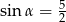 B)
B) 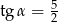 C)
C) 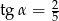 D)
D) 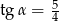
Rozwiąż równanie 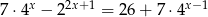 .
.
Średnia arytmetyczna ocen Jacka jest równa 3,75, a średnia ocen Karola (liczona z dokładnie tej samej liczby ocen) jest równa 4,25. Średnia ocen obu chłopców jest równa
A) 3,95 B) 4,5 C) 4,0 D) 4,15
Średnia arytmetyczna ocen Zosi jest równa 2,8, a średnia ocen Basi (liczona z dokładnie tej samej liczby ocen) jest równa 4,4. Średnia ocen obu dziewcząt jest równa
A) 3,6 B) 4,0 C) 3,8 D) 4,15
Spośród liczb dwucyfrowych wybrano bez zwracania dwa razy po jednej liczbie. Oblicz prawdopodobieństwo, że dwa razy wybrano liczbę parzystą.
Spośród dodatnich liczb dwucyfrowych losujemy kolejno bez zwracania dwie liczby. Oblicz prawdopodobieństwo wylosowania dwóch liczb parzystych.
Rozwiąż nierówność
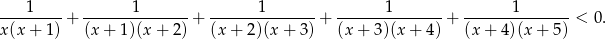
O zdarzeniach 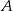 i
i 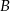 wiadomo, że
wiadomo, że 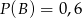 ,
, 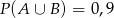 oraz
oraz 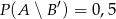 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 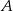 .
.
Podstawą ostrosłupa 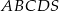 jest prostokąt
jest prostokąt 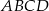 o bokach długości
o bokach długości 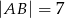 i
i 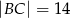 . Krawędź
. Krawędź 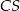 jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt
jest prostopadła do podstawy. Najdłuższa krawędź boczna tworzy z podstawą kąt 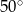 . Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość.
. Wykonaj rysunek pomocniczy tego ostrosłupa oraz oblicz jego objętość.
Uzasadnij, że nierówność 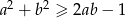 jest prawdziwa dla dowolnych liczb rzeczywistych
jest prawdziwa dla dowolnych liczb rzeczywistych  i
i 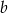 .
.
Wykaż, że dla każdej liczby rzeczywistej  różnej od 0 i każdej liczby rzeczywistej
różnej od 0 i każdej liczby rzeczywistej 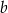 różnej od 0 spełniona jest nierówność
różnej od 0 spełniona jest nierówność
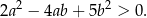
Wykaż, że dla każdych dwóch liczb rzeczywistych  i
i 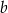 prawdziwa jest nierówność
prawdziwa jest nierówność
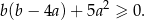
Wykaż, że dla każdych dwóch różnych liczb rzeczywistych  i
i 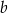 prawdziwa jest nierówność
prawdziwa jest nierówność
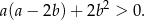
W pojemniku znajdują się losy loterii fantowej ponumerowane kolejnymi liczbami naturalnymi od 1000 do 9999. Każdy los, którego numer jest liczbą o sumie cyfr równej 3, jest wygrywający. Uczestnicy loterii losują z pojemnika po jednym losie. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że pierwszy los wyciągnięty z pojemnika był wygrywający.
W pojemniku znajdują się losy loterii fantowej ponumerowane kolejnymi liczbami naturalnymi od 2000 do 7000. Każdy los, którego numer jest liczbą o sumie cyfr równej 4, jest wygrywający. Uczestnicy loterii losują z pojemnika po jednym losie. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że pierwszy los wyciągnięty z pojemnika był wygrywający.
Pierwszy wyraz ciągu arytmetycznego 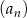 jest równy 4, a suma sześciu początkowych wyrazów tego ciągu wynosi 84.
jest równy 4, a suma sześciu początkowych wyrazów tego ciągu wynosi 84.
- Oblicz sumę pięćdziesięciu początkowych wyrazów tego ciągu.
- Dla jakiego
 liczby
liczby 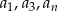 tworzą ciąg geometryczny?
tworzą ciąg geometryczny?
Pierwszy wyraz ciągu arytmetycznego 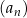 jest równy 2, a suma sześciu początkowych wyrazów tego ciągu wynosi 72.
jest równy 2, a suma sześciu początkowych wyrazów tego ciągu wynosi 72.
-
Oblicz sumę pięćdziesięciu początkowych wyrazów tego ciągu.
-
Dla jakiego
 liczby
liczby 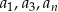 tworzą ciąg geometryczny?
tworzą ciąg geometryczny?
Mniejszą z dwóch liczb spełniających równanie 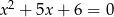 jest
jest
A) -6 B) -3 C) -2 D) -1
Mniejszą z dwóch liczb spełniających równanie 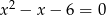 jest
jest
A) -6 B) -3 C) -2 D) -1
Mniejszą z dwóch liczb spełniających równanie 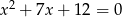 jest
jest
A) -4 B) -3 C) -2 D) -1
Liczba 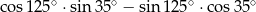 jest równa
jest równa
A) 1 B) 0 C) 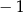 D)
D) 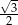
Osią symetrii paraboli będącej wykresem funkcji 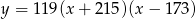 jest prosta o równaniu
jest prosta o równaniu
A) 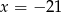 B)
B) 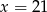 C)
C) 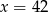 D)
D) 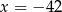
Osią symetrii paraboli będącej wykresem funkcji 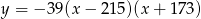 jest prosta o równaniu
jest prosta o równaniu
A) 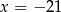 B)
B) 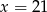 C)
C) 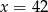 D)
D) 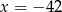
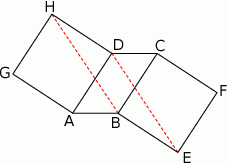
Na przeciwległych bokach równoległoboku 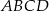 zbudowano kwadraty
zbudowano kwadraty 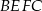 i
i 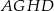 . Udowodnij, że proste
. Udowodnij, że proste 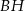 i
i 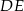 są równoległe.
są równoległe.
Wartość wyrażenia 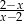 dla
dla 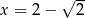 jest równa
jest równa
A) -1 B) 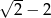 C)
C) 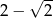 D) 1
D) 1
Wartość wyrażenia 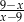 dla
dla 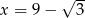 jest równa
jest równa
A) 1 B) 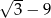 C)
C) 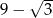 D) -1
D) -1
Odległość punktu 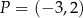 od prostej o równaniu
od prostej o równaniu 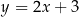 jest równa
jest równa
A) 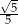 B)
B) 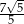 C)
C) 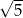 D) 5
D) 5
Odległość punktu 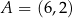 od prostej o równaniu
od prostej o równaniu 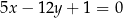 jest równa
jest równa
A) 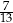 B)
B) 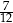 C)
C) 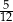 D)
D) 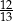
W trójkącie 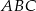 poprowadzono wysokości
poprowadzono wysokości 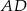 i
i 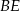 oraz dwusieczną
oraz dwusieczną 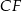 . Wiedząc, że
. Wiedząc, że 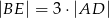 oblicz stosunek pól trójkątów
oblicz stosunek pól trójkątów 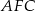 i
i 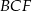 .
.
Podstawą ostrosłupa jest romb. Wysokość ostrosłupa ma długość 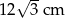 , a spodek
, a spodek 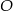 tej wysokości jest punktem przecięcia przekątnych. Każda ze ścian bocznych ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze
tej wysokości jest punktem przecięcia przekątnych. Każda ze ścian bocznych ostrosłupa tworzy z płaszczyzną podstawy kąt o mierze 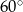 .
.
- Zaznacz na rysunku kąt nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa oraz poprowadź odcinek
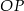 , którego długość jest równa odległości punktu
, którego długość jest równa odległości punktu 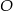 od ściany bocznej.
od ściany bocznej. - Oblicz odległość punktu
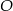 od ściany bocznej.
od ściany bocznej.