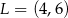Punkty 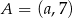 ,
, 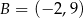 i
i 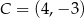 są wierzchołkami trójkąta równoramiennego o podstawie
są wierzchołkami trójkąta równoramiennego o podstawie 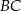 . Zatem
. Zatem
A) 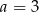 B)
B) 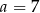 C)
C) 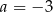 D)
D) 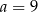
/Szkoła średnia/Zadania testowe/Geometria/Geometria analityczna/Trójkąt/Równoramienny
Prosta 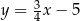 jest osią symetrii trójkąta
jest osią symetrii trójkąta 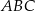 , w którym
, w którym 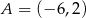 i
i 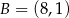 . Bok
. Bok 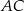 tego trójkąta jest zawarty w prostej o równaniu
tego trójkąta jest zawarty w prostej o równaniu
A) 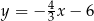 B)
B) 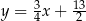 C)
C) 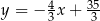 D)
D) 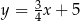
Punkt 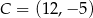 jest wierzchołkiem trójkąta równoramiennego, którego podstawa
jest wierzchołkiem trójkąta równoramiennego, którego podstawa 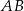 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 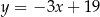 . Wysokość opuszczona na podstawę
. Wysokość opuszczona na podstawę 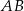 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu
A) 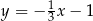 B)
B) 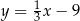 C)
C) 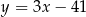 D)
D) 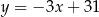
Punkty 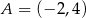 i
i 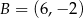 są końcami podstawy trójkąta równoramiennego
są końcami podstawy trójkąta równoramiennego 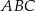 . Prosta zawierająca wysokość
. Prosta zawierająca wysokość 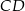 tego trójkąta przecina prostą
tego trójkąta przecina prostą 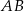 w punkcie
w punkcie
A) 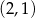 B)
B) 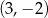 C)
C) 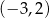 D)
D) 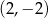
Punkty 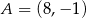 i
i 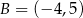 są końcami podstawy trójkąta równoramiennego
są końcami podstawy trójkąta równoramiennego 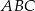 . Prosta zawierająca wysokość
. Prosta zawierająca wysokość 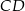 tego trójkąta przecina prostą
tego trójkąta przecina prostą 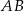 w punkcie
w punkcie
A) 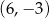 B)
B) 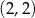 C)
C) 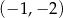 D)
D) 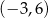
Punkt 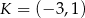 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 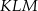 , w którym
, w którym 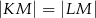 . Odcinek
. Odcinek 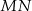 jest wysokością trójkąta i
jest wysokością trójkąta i 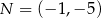 . Zatem
. Zatem
A) 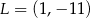 B)
B) 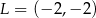 C)
C) 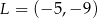 D)
D) 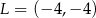
Punkt 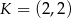 jest wierzchołkiem trójkąta równoramiennego
jest wierzchołkiem trójkąta równoramiennego 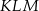 , w którym
, w którym 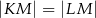 . Odcinek
. Odcinek 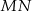 jest wysokością trójkąta i
jest wysokością trójkąta i 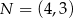 . Zatem
. Zatem
A) 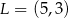 B)
B) 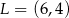 C)
C) 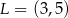 D)
D)