Pierwiastkami wielomianu stopnia trzeciego są liczby 1, 3, 5. Współczynnik przy najwyższej potędze zmiennej tego wielomianu jest równy 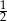 . Uzasadnij, że dla każdej liczby całkowitej nieparzystej wartość tego wielomianu jest liczbą podzielną przez 24.
. Uzasadnij, że dla każdej liczby całkowitej nieparzystej wartość tego wielomianu jest liczbą podzielną przez 24.
/Szkoła średnia/Funkcje/Wielomiany/Stopnia 3
Dane są wielomiany 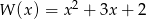 ,
, 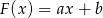 ,
, 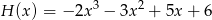 . Wyznacz współczynniki
. Wyznacz współczynniki 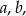 dla których wielomiany
dla których wielomiany 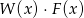 oraz
oraz 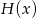 są równe.
są równe.
Dane są wielomiany 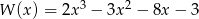 i
i 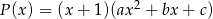 .
.
- Wyznacz współczynniki
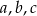 tak, aby
tak, aby 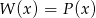 .
. - Przedstaw wielomian
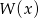 jako iloczyn wielomianów liniowych.
jako iloczyn wielomianów liniowych.
Dany jest wielomian 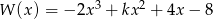 .
.
- Wyznacz wartość
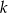 tak, aby reszta z dzielenia wielomianu W przez dwumian
tak, aby reszta z dzielenia wielomianu W przez dwumian 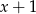 była równa -6.
była równa -6. - Dla znalezionej wartości
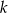 rozłóż wielomian na czynniki liniowe.
rozłóż wielomian na czynniki liniowe. - Dla znalezionej wartości
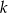 rozwiąż nierówność
rozwiąż nierówność 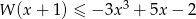 .
.
Wyznacz współczynniki 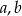 wielomianu
wielomianu 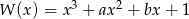 wiedząc, że dla każdego
wiedząc, że dla każdego 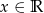 prawdziwa jest równość:
prawdziwa jest równość: 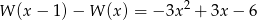 .
.
Wielomian 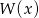 stopnia 3 jest podzielny przez trójmian kwadratowy
stopnia 3 jest podzielny przez trójmian kwadratowy 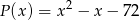 . Wiadomo ponadto, że
. Wiadomo ponadto, że 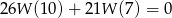 . Wyznacz miejsca zerowe wielomianu
. Wyznacz miejsca zerowe wielomianu 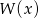 .
.
Wielomian 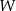 dany jest wzorem
dany jest wzorem 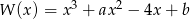 .
.
- Wyznacz
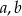 oraz
oraz  tak, aby wielomian
tak, aby wielomian 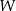 był równy wielomianowi
był równy wielomianowi 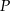 , gdy
, gdy 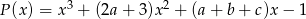 .
. - Dla
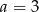 i
i 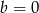 zapisz wielomian
zapisz wielomian 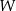 w postaci iloczynu trzech wielomianów stopnia pierwszego.
w postaci iloczynu trzech wielomianów stopnia pierwszego.
Maksymalny przedział, na którym funkcja 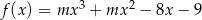 jest malejąca ma długość 2. Oblicz wartość parametru
jest malejąca ma długość 2. Oblicz wartość parametru 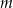 oraz wyznacz największą wartość funkcji na przedziale
oraz wyznacz największą wartość funkcji na przedziale 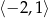 .
.
Rozłóż wielomian 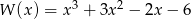 na czynniki liniowe.
na czynniki liniowe.
Korzystając z definicji funkcji rożnowartościowej wykaż, że funkcja 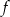 określona wzorem
określona wzorem 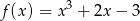 jest rożnowartościowa.
jest rożnowartościowa.
Dany jest wielomian 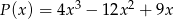 , gdzie
, gdzie 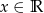 .
.
- Dla jakich argumentów wielomian
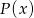 przyjmuje wartość równą 27?
przyjmuje wartość równą 27? - Wielomiany
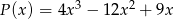 oraz
oraz 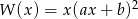 są równe. Wyznacz
są równe. Wyznacz  i
i 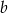 .
.
Wielomian 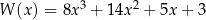 jest iloczynem wielomianów
jest iloczynem wielomianów 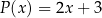 oraz
oraz 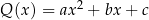 . Oblicz wartości współczynników:
. Oblicz wartości współczynników: 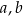 oraz
oraz  .
.
Wielomiany 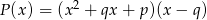 i
i 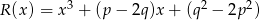 są równe. Oblicz
są równe. Oblicz 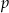 i
i 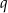 .
.
Sprawdź, czy równe są wielomiany 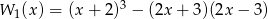 i
i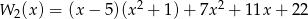 .
.
Wielomian 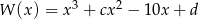 jest podzielny przez dwumian
jest podzielny przez dwumian 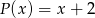 . Przy dzieleniu wielomianu
. Przy dzieleniu wielomianu 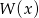 przez dwumian
przez dwumian 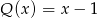 otrzymujemy resztę
otrzymujemy resztę 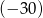 . Oblicz pierwiastki wielomianu
. Oblicz pierwiastki wielomianu 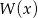 i rozwiąż nierówność
i rozwiąż nierówność 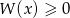 .
.
Dany jest wielomian 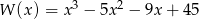 .
.
- Sprawdź, czy punkt
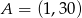 należy do wykresu tego wielomianu.
należy do wykresu tego wielomianu. - Zapisz wielomian
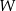 w postaci iloczynu trzech wielomianów stopnia pierwszego.
w postaci iloczynu trzech wielomianów stopnia pierwszego.
Dany jest wielomian 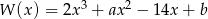 .
.
- Dla
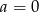 i
i 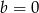 otrzymamy wielomian
otrzymamy wielomian 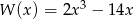 . Rozwiąż równanie
. Rozwiąż równanie 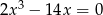 .
. - Dobierz wartości
 i
i 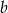 tak, aby wielomian
tak, aby wielomian 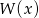 był podzielny jednocześnie przez
był podzielny jednocześnie przez 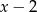 oraz
oraz 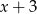 .
.
Wielomian 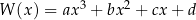 jest iloczynem wielomianów
jest iloczynem wielomianów 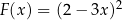 oraz
oraz 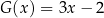 . Oblicz sumę
. Oblicz sumę 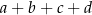 współczynników wielomianu
współczynników wielomianu 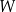 .
.
Wielomiany 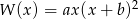 i
i 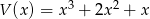 są równe. Oblicz
są równe. Oblicz  i
i 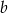 .
.
Dany jest wielomian 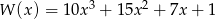 .
.
- Zapisz wielomian
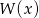 jako iloczyn wielomianów liniowych.
jako iloczyn wielomianów liniowych. - Określ dziedzinę funkcji
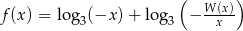 .
.

