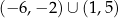Na rysunku przedstawiono wykres funkcji  .
.
Iloczyn 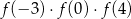 jest równy
jest równy
A) 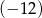 B)
B) 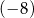 C) 0 D) 16
C) 0 D) 16
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
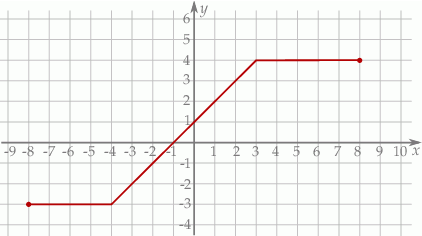
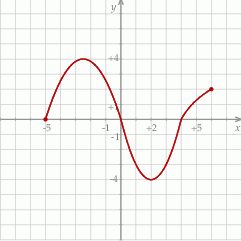
Na rysunku przedstawiono wykres funkcji 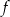 .
.

Iloczyn 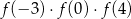 jest równy
jest równy
A) 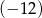 B)
B) 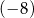 C) 0 D) 16
C) 0 D) 16
Wskaż rysunek, na którym przedstawiono fragment wykresu funkcji
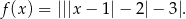
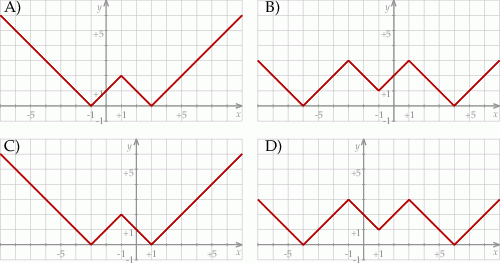
Rysunek przedstawia wykres funkcji 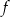 .
.
Na podstawie rysunku można stwierdzić, że
A) dziedzina funkcji to 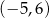 B)
B) 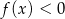 dla
dla 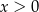
C) funkcja ma dwa miejsca zerowe D) zbiór wartości funkcji to 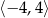
Na rysunku przedstawiono wykres funkcji 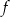 określonej w zbiorze
określonej w zbiorze 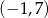 .
.
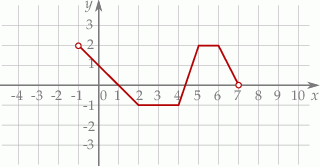
Wskaż zdanie prawdziwe.
A) Funkcja 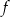 ma trzy miejsca zerowe.
ma trzy miejsca zerowe.
B) Zbiorem wartości funkcji 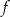 jest
jest 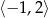 .
.
C) Funkcja 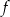 nie przyjmuje wartości 2.
nie przyjmuje wartości 2.
D) Funkcja 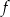 osiąga wartości dodatnie dla argumentów ze zbioru
osiąga wartości dodatnie dla argumentów ze zbioru 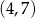 .
.
Na rysunku przedstawiono wykres funkcji 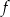 określonej w zbiorze
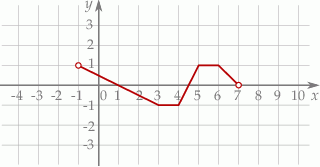
określonej w zbiorze 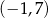 .
.
Wskaż zdanie prawdziwe.
A) Funkcja  ma trzy miejsca zerowe.
ma trzy miejsca zerowe.
B) Zbiorem wartości funkcji 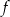 jest
jest 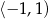 .
.
C) Funkcja 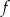 osiąga wartość największą równą 1.
osiąga wartość największą równą 1.
D) Funkcja 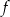 osiąga wartości ujemne dla argumentów ze zbioru
osiąga wartości ujemne dla argumentów ze zbioru 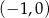 .
.
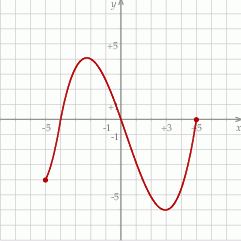
Na wykresie przedstawiono wykres funkcji 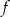 .
.
Wskaż zdanie prawdziwe.
A) Dziedziną funkcji  jest przedział
jest przedział 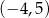 .
.
B) Funkcja 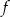 ma dwa miejsca zerowe.
ma dwa miejsca zerowe.
C) Funkcja 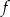 dla argumentu 1 przyjmuje wartość
dla argumentu 1 przyjmuje wartość 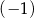 .
.
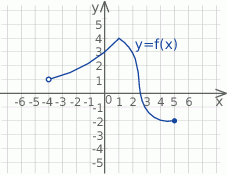
D) Zbiorem wartości funkcji 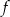 jest przedział
jest przedział ![(− 4,5]](https://img.zadania.info/zad/3523914/HzadT8x.gif) .
.
Rysunek przedstawia wykres funkcji 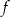 .
.
Na podstawie rysunku można stwierdzić, że
A) dziedzina funkcji to 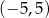 B)
B) 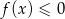 dla
dla 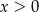
C) funkcja ma dwa miejsca zerowe D) zbiór wartości funkcji to 
Rysunek przedstawia wykres funkcji  .
.
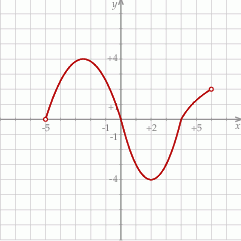
Na podstawie rysunku można stwierdzić, że
A) dziedzina funkcji to 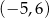 B)
B) 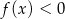 dla
dla 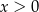
C) funkcja ma trzy miejsca zerowe D) zbiór wartości funkcji to 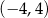
W kartezjańskim układzie współrzędnych 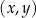 narysowano wykres funkcji
narysowano wykres funkcji 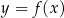 (zobacz rysunek).
(zobacz rysunek).
Wskaż przedział, który nie zawiera się w dziedzinie funkcji 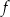 .
.
A) ![[− 6,− 4]](https://img.zadania.info/zad/3001188/HzadT4x.png) B)
B) ![[− 5,− 3]](https://img.zadania.info/zad/3001188/HzadT5x.png) C)
C) ![[− 1,3]](https://img.zadania.info/zad/3001188/HzadT6x.png) D)
D) ![[3,5]](https://img.zadania.info/zad/3001188/HzadT7x.png)
Wskaż wykres funkcji, która w przedziale 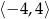 ma dokładnie jedno miejsce zerowe.
ma dokładnie jedno miejsce zerowe.
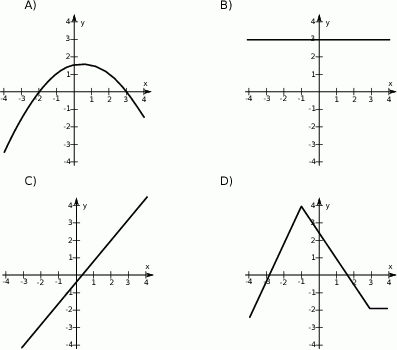
Wskaż wykres funkcji, która w przedziale  ma dokładnie dwa miejsca zerowe.
ma dokładnie dwa miejsca zerowe.
Wskaż wykres funkcji, która w przedziale 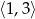 ma dokładnie jedno miejsce zerowe.
ma dokładnie jedno miejsce zerowe.
Na rysunku przedstawiony jest wykres funkcji  . Dziedziną funkcji
. Dziedziną funkcji  , gdzie
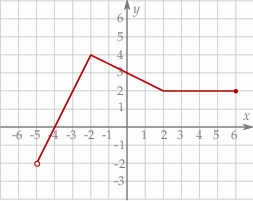
, gdzie 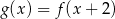 jest zbiór
jest zbiór
A) 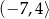 B)
B)  C)
C) 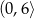 D)
D) 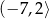
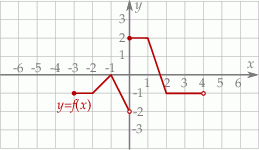
Jeśli na rysunku przedstawiony jest wykres funkcji 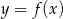 , to dziedziną funkcji
, to dziedziną funkcji 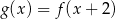 jest zbiór
jest zbiór
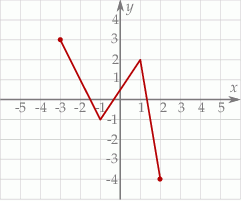
A) 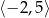 B)
B) 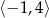 C)
C)  D)
D) 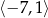
Jeśli na rysunku przedstawiony jest wykres funkcji 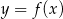 , to dziedziną funkcji
, to dziedziną funkcji 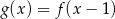 jest zbiór
jest zbiór
A) 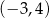 B)
B) 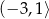 C)
C) 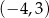 D)
D) 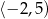
Na rysunku przedstawiony jest wykres funkcji 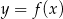 . Dziedziną funkcji
. Dziedziną funkcji  , gdzie
, gdzie  jest zbiór
jest zbiór
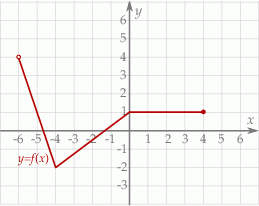
A) 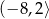 B)
B) 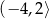 C)
C) 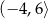 D)
D) 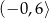
Na rysunku przedstawiony jest wykres funkcji 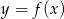 . Dziedziną funkcji
. Dziedziną funkcji 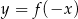 jest
jest
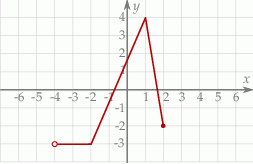
A) 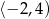 B)
B) 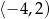 C)
C) 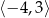 D)
D) 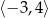
Dany jest wykres funkcji 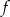 . Dziedziną funkcji
. Dziedziną funkcji 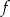 jest przedział
jest przedział
A) 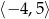 B)
B)  C)
C) 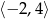 D)
D) 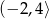
Dziedziną funkcji, której wykres przedstawiono na rysunku jest
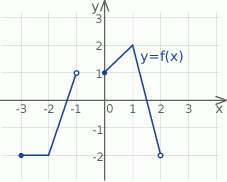
A) 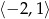 B)
B) 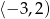 C)
C) 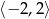 D)
D) 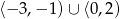
W kartezjańskim układzie współrzędnych 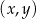 narysowano wykres funkcji
narysowano wykres funkcji 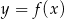 (zobacz rysunek).
(zobacz rysunek).
Dziedziną funkcji  jest zbiór
jest zbiór
A) ![[− 6,5]](https://img.zadania.info/zad/6322164/HzadT4x.gif) B)
B)  C)
C) ![(− 3,5]](https://img.zadania.info/zad/6322164/HzadT6x.gif) D)
D) ![[− 3,5]](https://img.zadania.info/zad/6322164/HzadT7x.gif)
Na rysunku przedstawiony jest wykres funkcji 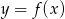 .
.
 jest przedział
jest przedział 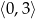 B)
B) 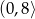 C)
C) 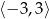 D)
D) 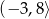
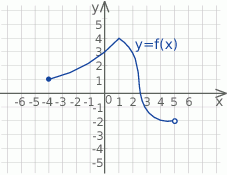
Na rysunku przedstawiono wykres funkcji 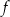 .
.
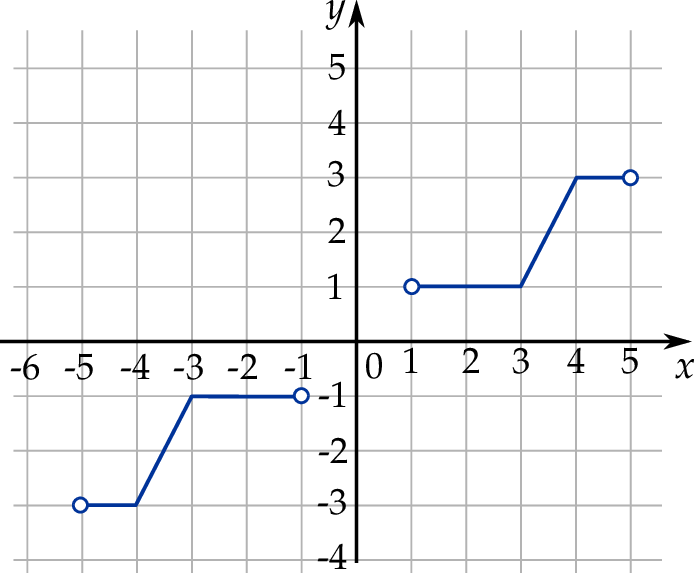
Dziedziną funkcji 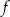 jest zbiór
jest zbiór
A) 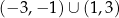 B)
B)  C)
C) 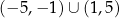 D)
D) 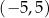
Dany jest wykres funkcji 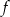 . Dziedziną funkcji
. Dziedziną funkcji 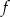 jest przedział
jest przedział
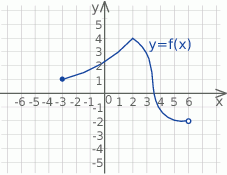
A) 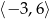 B)
B) 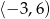 C)
C)  D)
D) 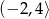
W kartezjańskim układzie współrzędnych  narysowano wykres funkcji
narysowano wykres funkcji 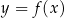 (zobacz rysunek).
(zobacz rysunek).
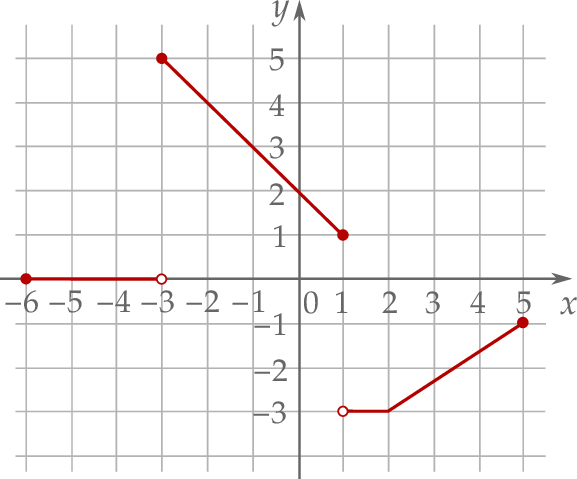
Dziedziną funkcji 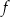 jest zbiór
jest zbiór
A) 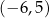 B)
B) ![[− 6,5]](https://img.zadania.info/zad/9554435/HzadT5x.png) C)
C) ![(− 3,5]](https://img.zadania.info/zad/9554435/HzadT6x.png) D)
D) ![[− 3,5]](https://img.zadania.info/zad/9554435/HzadT7x.png)
Dany jest wykres funkcji 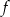 . Dziedziną funkcji
. Dziedziną funkcji 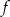 jest przedział
jest przedział
A) 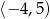 B)
B) 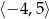 C)
C) 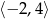 D)
D) 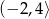
Na rysunku przedstawiony jest wykres funkcji 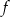 .
.
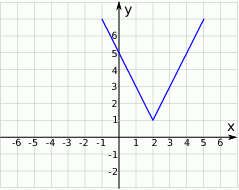
Wskaż wzór funkcji, której wykres jest symetryczny do wykresu funkcji 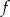 względem osi
względem osi 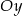 układu współrzędnych.
układu współrzędnych.
A) 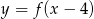 B)
B) 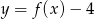 C)
C) 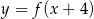 D)
D) 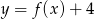
Na rysunku przedstawiono wykres funkcji 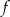 określonej w zbiorze
określonej w zbiorze 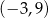 .
.
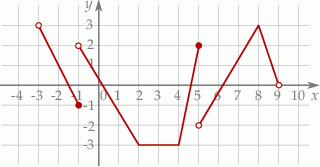
Wskaż zdanie prawdziwe.
A) Zbiorem wartości funkcji  jest przedział
jest przedział 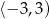
B) Funkcje 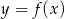 i
i 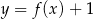 mają tyle samo miejsc zerowych
mają tyle samo miejsc zerowych
C) Funkcja 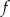 osiąga wartość równą 2 w trzech punktach.
osiąga wartość równą 2 w trzech punktach.
D) Wartość funkcji 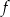 dla argumentu
dla argumentu 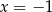 jest liczbą dodatnią.
jest liczbą dodatnią.
W kartezjańskim układzie współrzędnych 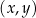 narysowano wykres funkcji
narysowano wykres funkcji 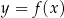 (zobacz rysunek).
(zobacz rysunek).
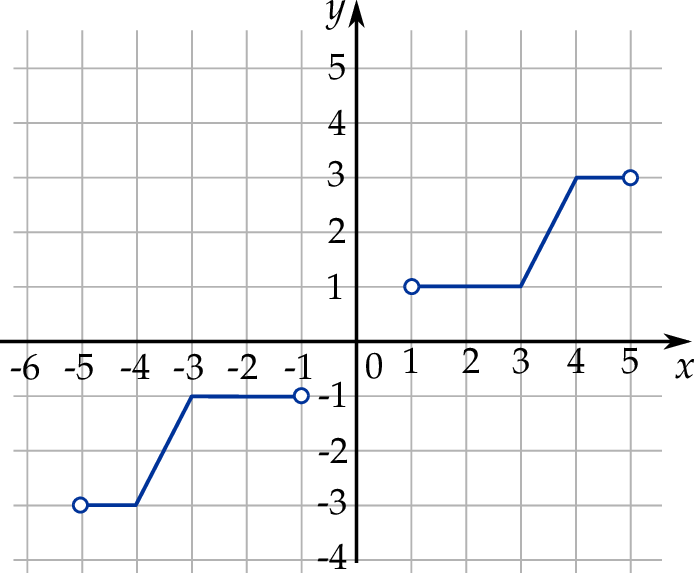
Dziedziną funkcji 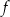 jest zbiór
jest zbiór
A) ![[− 3,− 1]∪ [1,3]](https://img.zadania.info/zad/9424758/HzadT4x.png) B)
B) 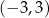 C)
C) 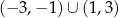
D) ![[− 5,− 1]∪ [1,5]](https://img.zadania.info/zad/9424758/HzadT7x.png) E)
E) 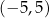 F)
F) 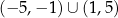
W kartezjańskim układzie współrzędnych 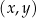 narysowano wykres funkcji
narysowano wykres funkcji 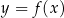 (zobacz rysunek).
(zobacz rysunek).
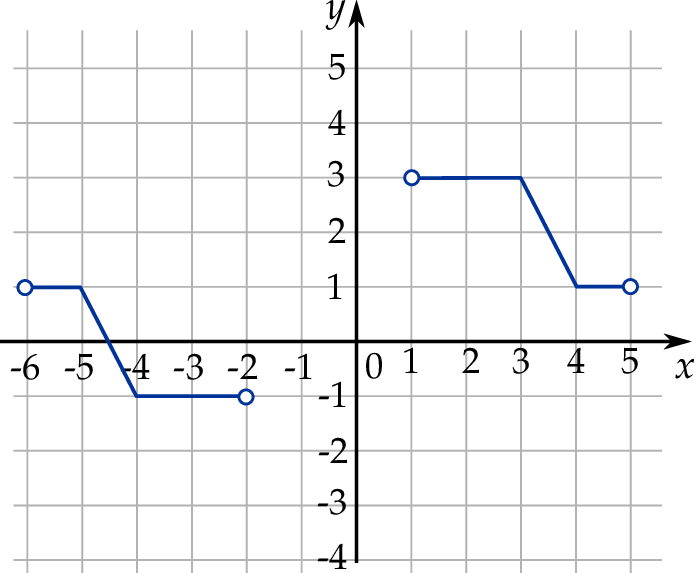
Dziedziną funkcji 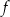 jest zbiór
jest zbiór
A) ![[− 1,1)∪ (1 ,3]](https://img.zadania.info/zad/3488637/HzadT4x.png) B)
B) ![[− 1,3]](https://img.zadania.info/zad/3488637/HzadT5x.png) C)
C) 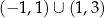
D) ![[− 5,− 1]∪ [1,5]](https://img.zadania.info/zad/3488637/HzadT7x.png) E)
E) 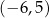 F)
F)