Karol ułożył figurę przedstawioną na rysunku. Figura została zbudowana z dwóch rodzajów klocków: sześciennych i prostopadłościennych. Wszystkie klocki tego samego rodzaju mają takie same wymiary.
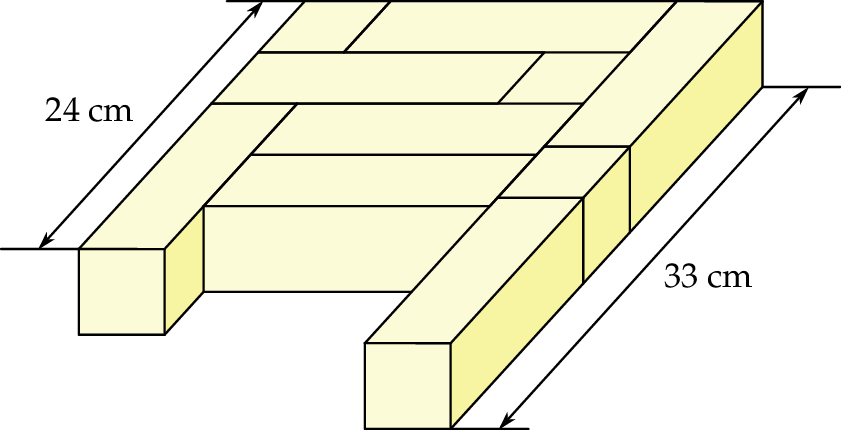
Oblicz objętość bryły zbudowanej z tych klocków.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Karol ułożył figurę przedstawioną na rysunku. Figura została zbudowana z dwóch rodzajów klocków: sześciennych i prostopadłościennych. Wszystkie klocki tego samego rodzaju mają takie same wymiary.

Oblicz objętość bryły zbudowanej z tych klocków.
Mrówka przeszła po powierzchni sześcianu z wierzchołka 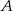 do wierzchołka będącego drugim końcem przekątnej sześcianu wychodzącej z wierzchołka
do wierzchołka będącego drugim końcem przekątnej sześcianu wychodzącej z wierzchołka 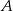 , przy czym była to droga najkrótsza. Narysuj siatkę sześcianu i oblicz odległość, jaką pokonała mrówka, jeżeli krawędź sześcianu ma długość
, przy czym była to droga najkrótsza. Narysuj siatkę sześcianu i oblicz odległość, jaką pokonała mrówka, jeżeli krawędź sześcianu ma długość 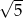 .
.
Oblicz objętość i pole powierzchni graniastosłupa prostego, którego podstawą jest romb o przekątnych długości 6 cm i 8 cm, którego przekątna ściany bocznej tworzy z krawędzią podstawy kąt o mierze 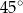 .
.
Na rysunku przedstawiono fragment siatki graniastosłupa prawidłowego trójkątnego.
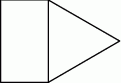
Pole narysowanego trójkąta jest równe 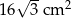 , a pole prostokąta jest równe
, a pole prostokąta jest równe 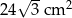 . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
Trójkąt równoramienny o kącie 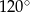 i ramieniu długości 6 obrócono względem zewnętrznej wysokości, otrzymując wydrążoną bryłę. Oblicz objętość tej bryły.
i ramieniu długości 6 obrócono względem zewnętrznej wysokości, otrzymując wydrążoną bryłę. Oblicz objętość tej bryły.
Graniastosłup prawidłowy czworokątny przecięto płaszczyzną, która zawiera krawędź podstawy oraz przechodzi przez środek przeciwległej krawędzi bocznej (zobacz rysunek).
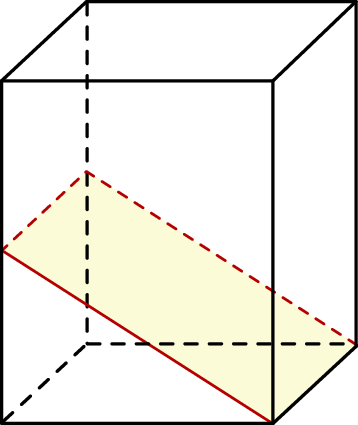
Oblicz jaki jest stosunek objętości dwóch brył na jakie został podzielony ten graniastosłup.
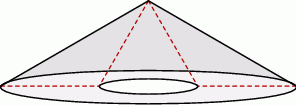
Przekrój osiowy stożka jest trójkątem równobocznym o polu 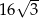 . Oblicz objętość i pole powierzchni całkowitej tego stożka.
. Oblicz objętość i pole powierzchni całkowitej tego stożka.
Pole powierzchni bocznej ostrosłupa prawidłowego czworokątnego jest równe 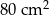 , a pole jego powierzchni całkowitej wynosi
, a pole jego powierzchni całkowitej wynosi 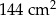 . Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa. Zapisz obliczenia.
. Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa. Zapisz obliczenia.
Pole powierzchni czworościanu foremnego jest równe 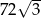 . Oblicz długość krawędzi tego czworościanu.
. Oblicz długość krawędzi tego czworościanu.
Objętość prostopadłościanu jest równa 405. Stosunki długości krawędzi prostopadłościanu wychodzących z tego samego wierzchołka prostopadłościanu to 1 : 3 : 5. Oblicz pole powierzchni całkowitej prostopadłościanu.
Po rozklejeniu ściany bocznej pudełka mającego kształt walca otrzymano równoległobok. Jeden z boków tej figury ma długość 44 cm, a jej pole jest równe 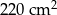 . Oblicz objętość tego pudełka. Przyjmij przybliżenie
. Oblicz objętość tego pudełka. Przyjmij przybliżenie 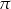 równe
równe 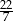 . Zapisz obliczenia.
. Zapisz obliczenia.

Po rozklejeniu ściany bocznej pudełka mającego kształt walca otrzymano równoległobok. Jeden z boków tej figury ma długość 33 cm, a jej pole jest równe 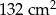 . Oblicz objętość tego pudełka. Przyjmij przybliżenie
. Oblicz objętość tego pudełka. Przyjmij przybliżenie 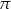 równe
równe 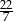 . Zapisz obliczenia.
. Zapisz obliczenia.

Metalową kulę o promieniu 10 cm i stożek o średnicy 16 cm i wysokości 12 cm przetopiono. Następnie z otrzymanego metalu wykonano walec o średnicy 8 cm. Jaką wysokość ma ten walec?
Metalową kulę o promieniu 5 cm i stożek o średnicy 12 cm i wysokości 15 cm przetopiono. Następnie z otrzymanego metalu wykonano walec o średnicy 8 cm. Jaką wysokość ma ten walec?
Na rysunku przedstawiono graniastosłup prosty, którego podstawą jest prostokąt.
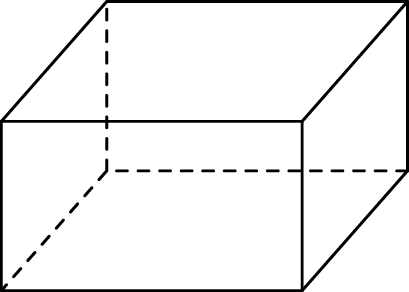
Jeden z boków tego prostokąta ma długość 16 cm, a długość jego przekątnej jest równa 20 cm. Przekątna najmniejszej ściany bocznej graniastosłupa ma długość 15 cm. Oblicz sumę długości wszystkich krawędzi tego graniastosłupa.
Oblicz objętość graniastosłupa prostego, którego podstawą jest romb o przekątnych długości 16 cm i 30 cm, a krawędź boczna jest dwa razy dłuższa od krawędzi podstawy.
Na rysunku przedstawiono dwie różne ściany prostopadłościanu. Jedna jest kwadratem o boku 5 cm, a druga – prostokątem o bokach 3 cm i 5 cm.
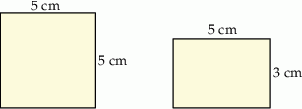
Oblicz sumę długości wszystkich krawędzi prostopadłościanu o takich wymiarach.
Na rysunku przedstawiono dwie różne ściany prostopadłościanu. Jedna jest prostokątem o bokach 6 cm i 9 cm, a druga – prostokątem o bokach 9 cm i 12 cm.
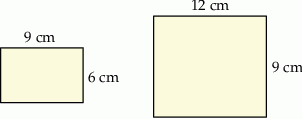
Oblicz pole powierzchni całkowitej prostopadłościanu o takich wymiarach.
Ile litrów wody można wlać do garnka w kształcie walca o średnicy 24 cm i wysokości 15 cm?
Suma wszystkich krawędzi ostrosłupa prawidłowego trójkątnego wynosi 72 cm. Oblicz długość krawędzi podstawy tego ostrosłupa, jeśli krawędź boczna ma długość 16 cm.
Dany jest graniastosłup prawidłowy czworokątny, w którym zaznaczone podstawy są kwadratami. Suma długości jego krawędzi zaznaczonych pogrubioną linią na rysunku 1. jest równa 27 cm. Suma długości jego krawędzi zaznaczonych pogrubioną linią na rysunku 2. jest równa 30 cm.
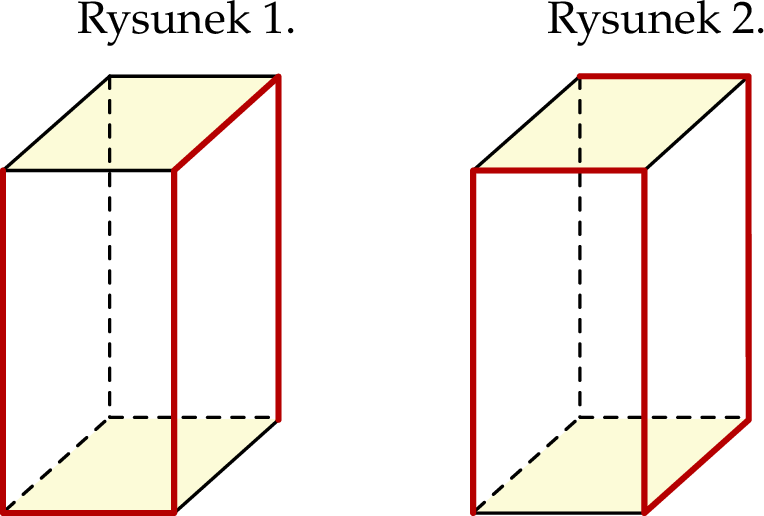
Oblicz objętość tego graniastosłupa.
Z czterech ołowianych sześcianów o przekątnej długości 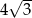 wykonano graniastosłup prawidłowy czworokątny o krawędzi podstawy długości 8. Oblicz długość przekątnej otrzymanego graniastosłupa.
wykonano graniastosłup prawidłowy czworokątny o krawędzi podstawy długości 8. Oblicz długość przekątnej otrzymanego graniastosłupa.
W graniastosłupie prawidłowym czworokątnym powierzchnia boczna po rozwinięciu jest kwadratem o polu 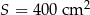 . Oblicz objętość i pole powierzchni całkowitej tej bryły .
. Oblicz objętość i pole powierzchni całkowitej tej bryły .
W graniastosłupie prawidłowym trójkątnym powierzchnia boczna po rozwinięciu jest kwadratem o polu 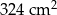 . Oblicz objętość tej bryły .
. Oblicz objętość tej bryły .
