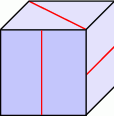
Oblicz pole powierzchni i objętość sześcianu, którego przekątna ma długość 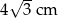 .
.
/Szkoła podstawowa/Geometria/Figury przestrzenne
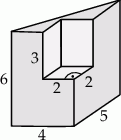
Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni tej bryły.
Pole powierzchni bocznej graniastosłupa prawidłowego czworokątnego jest 6 razy większe, od jego pola podstawy, a objętość tego graniastosłupa jest równa 12. Oblicz długość krawędzi podstawy oraz długość przekątnej tego graniastosłupa. Zapisz obliczenia.
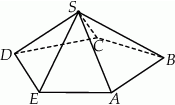
Dany jest ostrosłup o podstawie pięciokątnej  (zobacz rysunek). Każda ze ścian bocznych tego ostrosłupa jest trójkątem o polu trzy razy mniejszym niż pole pięciokąta
(zobacz rysunek). Każda ze ścian bocznych tego ostrosłupa jest trójkątem o polu trzy razy mniejszym niż pole pięciokąta  . Pole powierzchni całkowitej tego ostrosłupa jest równe 136. Oblicz pole jego podstawy.
. Pole powierzchni całkowitej tego ostrosłupa jest równe 136. Oblicz pole jego podstawy.
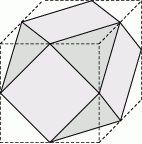
W kostce mającej kształt sześcianu o krawędzi długości 6 ścięto wszystkie naroża płaszczyznami przechodzącymi przez środki odpowiednich krawędzi (zobacz rysunek). Oblicz objętość otrzymanej bryły.
Cztery jednakowe prostopadłościenne klocki, każdy o wymiarach 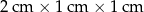 , ułożono tak, jak przedstawiono na rysunku.
, ułożono tak, jak przedstawiono na rysunku.
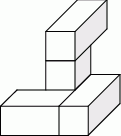
Następnie do tej budowli dołożono sześcienne klocki o krawędzi długości 1 cm tak, aby powstał prostopadłościan najmniejszy z możliwych. Ile sześciennych klocków o krawędzi długości 1 cm dołożono do tej budowli? Jakie są wymiary otrzymanego prostopadłościanu?
Cztery jednakowe prostopadłościenne klocki, każdy o wymiarach 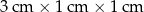 , ułożono tak, jak przedstawiono na rysunku.
, ułożono tak, jak przedstawiono na rysunku.
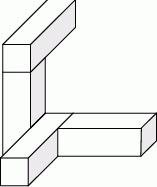
Następnie do tej budowli dołożono sześcienne klocki o krawędzi długości 1 cm tak, aby powstał prostopadłościan najmniejszy z możliwych. Ile sześciennych klocków o krawędzi długości 1 cm dołożono do tej budowli? Jakie są wymiary otrzymanego prostopadłościanu?
Graniastosłup prawidłowy trójkątny o krawędzi podstawy 4 cm i wysokości 10 cm przecięto płaszczyzną zawierającą wysokość podstawy i jedną z krawędzi bocznych. Jakie pole ma ten przekrój?
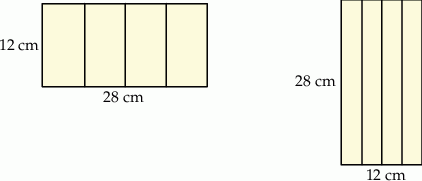
Maja zrobiła dwa pudełka w kształcie graniastosłupów prawidłowych czworokątnych o różnych objętościach. Powierzchnię boczną każdego z tych graniastosłupów wykonała z takich samych prostokątów o wymiarach 28 cm i 12 cm (patrz rysunek). Oblicz różnicę objętości tych graniastosłupów. Zapisz obliczenia.
Oskar zrobił dwa pudełka w kształcie graniastosłupów prawidłowych: czworokątnego i sześciokątnego. Powierzchnię boczną każdego z tych graniastosłupów wykonał z takich samych prostokątów o wymiarach 24 cm i 12 cm (patrz rysunek). Oblicz stosunek objętości tych graniastosłupów oraz ustal, który z nich ma większą objętość.

Pole powierzchni bocznej graniastosłupa prawidłowego sześciokątnego jest równe 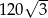 , a pole jego powierzchni całkowitej wynosi
, a pole jego powierzchni całkowitej wynosi 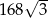 . Oblicz długość krawędzi podstawy i długość przekątnej ściany bocznej tego graniastosłupa. Zapisz obliczenia.
. Oblicz długość krawędzi podstawy i długość przekątnej ściany bocznej tego graniastosłupa. Zapisz obliczenia.
Długość promienia walca zmniejszono dziesięciokrotnie. Ile razy trzeba zwiększyć wysokość tego walca aby objętość się nie zmieniła?
Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni i objętość tej bryły.
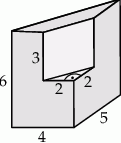
Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni i objętość tej bryły.
Pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego jest równe 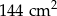 . Pole podstawy tej bryły stanowi 80% pola powierzchni bocznej tego ostrosłupa. Oblicz długość krawędzi podstawy tej bryły. Zapisz obliczenia.
. Pole podstawy tej bryły stanowi 80% pola powierzchni bocznej tego ostrosłupa. Oblicz długość krawędzi podstawy tej bryły. Zapisz obliczenia.
Na rysunku przedstawiono graniastosłup prosty, którego podstawą jest trójkąt prostokątny. Długość jednej z przyprostokątnych jest równa 8 cm, a długość przeciwprostokątnej jest równa 10 cm. Najmniejsza ściana boczna tego graniastosłupa ma pole równe 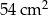 .
.

Oblicz sumę długości wszystkich krawędzi tego graniastosłupa.
Na rysunku przedstawiono graniastosłup prosty, którego podstawą jest trójkąt prostokątny. Długość jednej z przyprostokątnych jest równa 12 cm, a długość przeciwprostokątnej jest równa 15 cm. Najmniejsza ściana boczna tego graniastosłupa ma pole równe 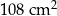 .
.

Oblicz sumę długości wszystkich krawędzi tego graniastosłupa.
Powierzchnia kartonu ma kształt prostokąta o wymiarach 8 cm i 15 cm. W czterech rogach tego kartonu wycięto kwadraty o boku 2,5 cm. Z pozostałej części złożono pudełko.

Oblicz objętość tego pudełka.
Pole powierzchni bocznej ostrosłupa prawidłowego trójkątnego jest równe 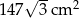 , a pole jego powierzchni całkowitej wynosi
, a pole jego powierzchni całkowitej wynosi 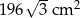 . Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa.
. Oblicz długość krawędzi podstawy i długość krawędzi bocznej tego ostrosłupa.
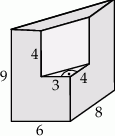
Oblicz objętość bryły, której kształt i wymiary przedstawiono na rysunku. Zapisz obliczenia.
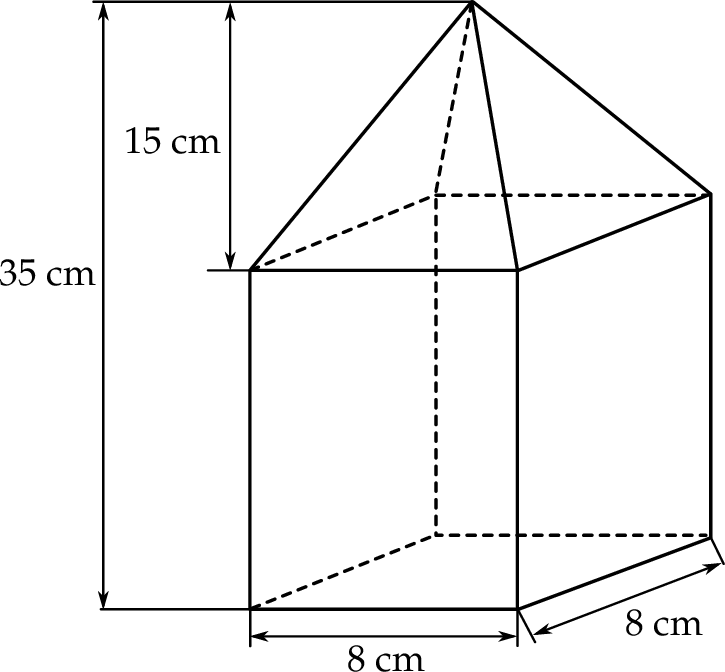
Oblicz objętość bryły, której kształt i wymiary przedstawiono na rysunku. Zapisz obliczenia.
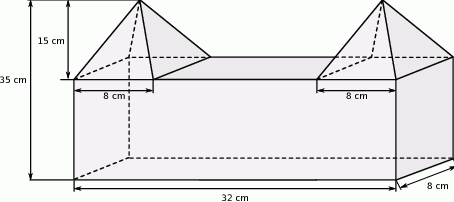
Na rysunku przedstawiono graniastosłup prosty o podstawie trójkąta prostokątnego i jego siatkę. Dwie dłuższe krawędzie podstawy graniastosłupa mają 12 cm i 13 cm długości, a pole zacieniowanej części siatki graniastosłupa jest równe 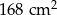 . Oblicz objętość tego graniastosłupa. Zapisz obliczenia.
. Oblicz objętość tego graniastosłupa. Zapisz obliczenia.
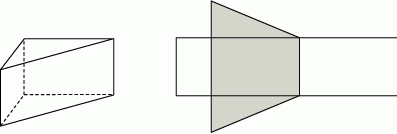
Na rysunku przedstawiono graniastosłup prosty o podstawie trójkąta prostokątnego i jego siatkę. Najkrótsza krawędź podstawy graniastosłupa ma długość 9 cm, a wysokość graniastosłupa ma długość 8 cm. Pole zacieniowanej części siatki graniastosłupa jest równe 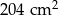 . Oblicz pole powierzchni całkowitej tego graniastosłupa. Zapisz obliczenia.
. Oblicz pole powierzchni całkowitej tego graniastosłupa. Zapisz obliczenia.
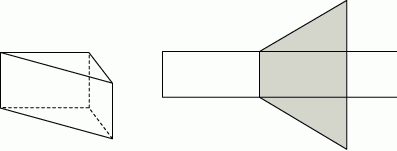
Na rysunku przedstawiono siatkę graniastosłupa prawidłowego czworokątnego oraz zapisano niektóre wymiary tej siatki.
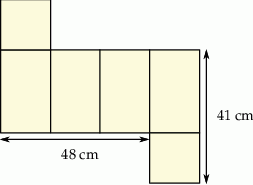
Oblicz objętość tego graniastosłupa.
Na rysunku przedstawiono siatkę graniastosłupa prawidłowego czworokątnego oraz zapisano niektóre wymiary tej siatki.
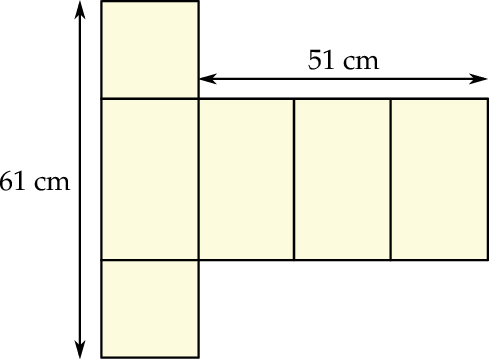
Oblicz objętość tego graniastosłupa.
Na rysunku przedstawiono siatkę graniastosłupa prostego, którego podstawą jest równoległobok. Na rysunku zapisano niektóre wymiary tej siatki.
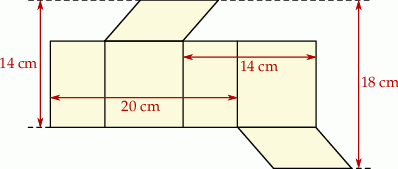
Oblicz objętość tego graniastosłupa.
Popatrz na kostkę przedstawioną na rysunku. Wiadomo, że na każdej ścianie narysowany jest odcinek oraz że odcinki na przeciwległych ścianach są równoległe. Narysuj siatkę z której można skleić tę kostkę. Na każdej ścianie narysuj odpowiedni odcinek.