Na rysunku przedstawiono dwa przystające prostokąty  i
i  o bokach długości 5 cm i 13 cm. Oblicz długość odcinka
o bokach długości 5 cm i 13 cm. Oblicz długość odcinka  .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku przedstawiono dwa przystające prostokąty  i
i  o bokach długości 5 cm i 13 cm. Oblicz długość odcinka
o bokach długości 5 cm i 13 cm. Oblicz długość odcinka  .
.

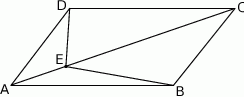
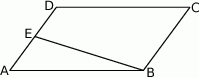
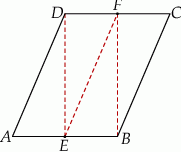
W równoległoboku 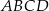 punkt
punkt 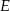 jest takim punktem boku
jest takim punktem boku 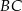 , że
, że 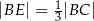 . Z wierzchołka
. Z wierzchołka 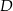 poprowadzono prostą przecinającą bok
poprowadzono prostą przecinającą bok 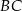 w punkcie
w punkcie 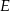 . Proste
. Proste 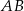 i
i 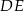 przecinają się w punkcie
przecinają się w punkcie 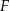 (zobacz rysunek). Wykaż, że pole trójkąta
(zobacz rysunek). Wykaż, że pole trójkąta 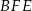 stanowi
stanowi 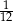 pola równoległoboku
pola równoległoboku 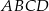 .
.
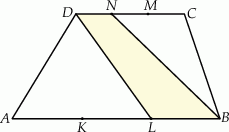
Punkty  i
i  dzielą podstawę
dzielą podstawę 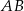 trapezu
trapezu 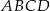 na trzy równe części, a punkty
na trzy równe części, a punkty 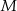 i
i 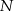 dzielą podstawę
dzielą podstawę 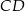 tego trapezu na trzy równe części. Pole czworokąta
tego trapezu na trzy równe części. Pole czworokąta 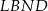 jest równe
jest równe 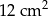 . Oblicz pole trapezu
. Oblicz pole trapezu 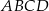 .
.
Punkt  jest środkiem boku
jest środkiem boku  równoległoboku
równoległoboku  , a odcinek
, a odcinek  przecina przekątną
przecina przekątną 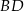 w punkcie
w punkcie 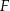 . Wykaż, że
. Wykaż, że 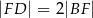 .
.
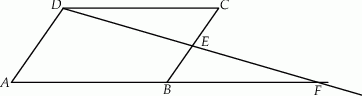
W równoległoboku 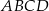 punkt
punkt 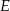 jest środkiem boku
jest środkiem boku 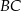 . Z wierzchołka
. Z wierzchołka 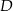 poprowadzono prostą przecinającą bok
poprowadzono prostą przecinającą bok 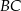 w punkcie
w punkcie 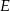 . Proste
. Proste 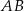 i
i 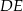 przecinają się w punkcie
przecinają się w punkcie 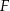 (zobacz rysunek). Wykaż, że punkt
(zobacz rysunek). Wykaż, że punkt  jest środkiem odcinka
jest środkiem odcinka  .
.
Punkty  i
i 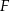 są środkami boków
są środkami boków 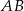 i
i 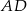 deltoidu
deltoidu 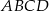 . Pole trójkąta
. Pole trójkąta 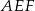 jest równe 3. Oblicz pole deltoidu
jest równe 3. Oblicz pole deltoidu 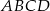 .
.
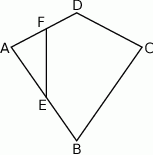
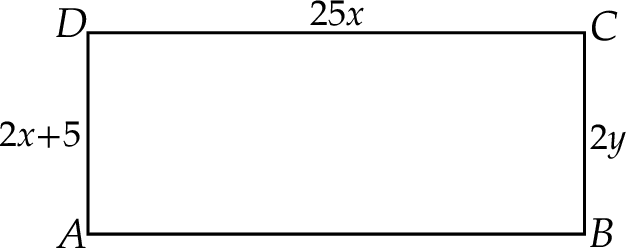
Wyznacz pole narysowanego prostokąta, jeżeli 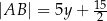 .
.
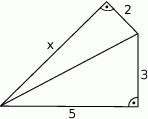
Oblicz długość odcinka  .
.
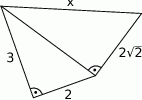
Oblicz długość odcinka  .
.
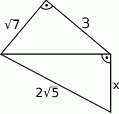
Oblicz długość odcinka  .
.
Punkt 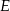 jest środkiem boku
jest środkiem boku 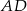 równoległoboku
równoległoboku 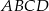 . Pole trójkąta
. Pole trójkąta 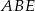 jest równe 2. Oblicz pole równoległoboku.
jest równe 2. Oblicz pole równoległoboku.
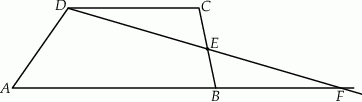
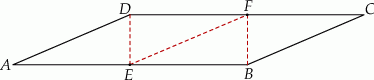
W trapezie  punkt
punkt  jest środkiem ramienia
jest środkiem ramienia  . Z wierzchołka
. Z wierzchołka 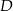 poprowadzono prostą przecinającą ramię
poprowadzono prostą przecinającą ramię 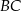 w punkcie
w punkcie 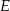 . Proste
. Proste 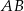 i
i 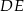 przecinają się w punkcie
przecinają się w punkcie 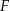 (zobacz rysunek). Wykaż, że
(zobacz rysunek). Wykaż, że 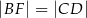 .
.
Równoległobok 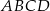 zbudowano z czterech przystających trójkątów prostokątnych (patrz rysunek). Boki równoległoboku mają długości
zbudowano z czterech przystających trójkątów prostokątnych (patrz rysunek). Boki równoległoboku mają długości  i
i  .
.
Oblicz pole równoległoboku 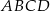 .
.
Równoległobok 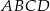 zbudowano z czterech przystających trójkątów prostokątnych (patrz rysunek). Boki równoległoboku mają długości
zbudowano z czterech przystających trójkątów prostokątnych (patrz rysunek). Boki równoległoboku mają długości 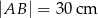 i
i 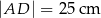 .
.
Oblicz pole równoległoboku  .
.
Równoległobok  o bokach długości 6 cm i 9 cm rozcięto wzdłuż prostej
o bokach długości 6 cm i 9 cm rozcięto wzdłuż prostej  na dwa trapezy tak, jak pokazano na rysunku. Odcinek
na dwa trapezy tak, jak pokazano na rysunku. Odcinek  ma długość 4,8 cm.
ma długość 4,8 cm.
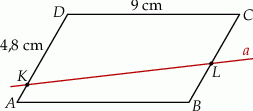
Pole trapezu  jest trzykrotnie mniejsze od pola równoległoboku
jest trzykrotnie mniejsze od pola równoległoboku  . Oblicz długość odcinka
. Oblicz długość odcinka  . Zapisz obliczenia.
. Zapisz obliczenia.
Ada wycięła z kartonu równoległobok 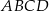 o bokach
o bokach 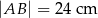 ,
, 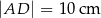 i polu równym
i polu równym 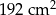 (rysunek I). Następnie rozcięła ten równoległobok na dwie pary przystających trapezów i złożyła z tych trapezów wielokąt przedstawiony na rysunku II. Od tego wielokąta odcięła dolną część wzdłuż jego przekątnej
(rysunek I). Następnie rozcięła ten równoległobok na dwie pary przystających trapezów i złożyła z tych trapezów wielokąt przedstawiony na rysunku II. Od tego wielokąta odcięła dolną część wzdłuż jego przekątnej 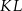 i otrzymała w ten sposób wielokąt przedstawiony na rysunku III.
i otrzymała w ten sposób wielokąt przedstawiony na rysunku III.
Oblicz obwód wielokąta z rysunku III.
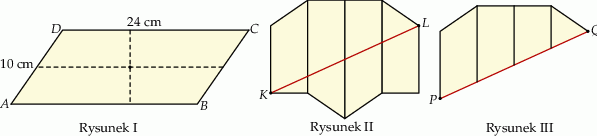
Oblicz pole i obwód równoległoboku przedstawionego na rysunku.
Oblicz pole i obwód równoległoboku przedstawionego na rysunku.
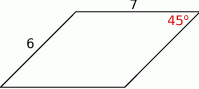
Oblicz pole i obwód równoległoboku przedstawionego na rysunku.
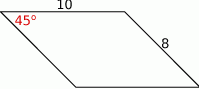
Boki trapezu równoramiennego mają długości 5 cm, 6 cm, 5 cm i 12 cm. Oblicz pole tego trapezu.
Boki trapezu równoramiennego mają długości 10 cm, 5 cm, 10 cm i 17 cm. Oblicz pole tego trapezu.
Wyznacz kąty trapezu równoramiennego, jeśli miara jednego z nich jest większa od miary drugiego o 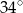 .
.
Wyznacz kąty trapezu równoramiennego, jeśli miara jednego z nich jest większa od miary drugiego o 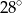 .
.
Wyznacz kąty trapezu równoramiennego, jeśli miara jednego z nich jest 5 razy większa od miary drugiego.
Wyznacz kąty trapezu równoramiennego, jeśli miara jednego z nich jest 4 razy większa od miary drugiego.
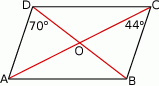
Oblicz miarę kąta ostrego, pod którym przecinają się przekątne równoległoboku przedstawionego na rysunku.
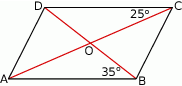
Oblicz miarę kąta ostrego, pod którym przecinają się przekątne równoległoboku przedstawionego na rysunku.
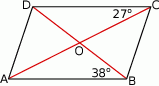
Oblicz miarę kąta rozwartego, pod którym przecinają się przekątne równoległoboku przedstawionego na rysunku.
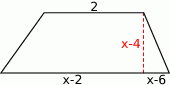
Pole trapezu przedstawionego na rysunku jest równe 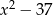 . Oblicz
. Oblicz  .
.
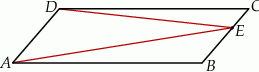
Na rysunku przedstawiono równoległobok 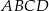 i trójkąt
i trójkąt 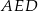 . Punkt
. Punkt 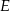 leży na odcinku
leży na odcinku 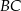 . Uzasadnij, że pole równoległoboku
. Uzasadnij, że pole równoległoboku  jest dwa razy większe od pola trójkąta
jest dwa razy większe od pola trójkąta  .
.
Trapez równoramienny  , którego pole jest równe
, którego pole jest równe 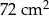 , podzielono na trójkąt
, podzielono na trójkąt 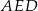 i trapez
i trapez 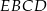 . Odcinek
. Odcinek 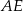 ma długość równą 4 cm, a odcinek
ma długość równą 4 cm, a odcinek 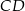 jest od niego 2 razy dłuższy. Oblicz pole trójkąta
jest od niego 2 razy dłuższy. Oblicz pole trójkąta 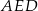 .
.
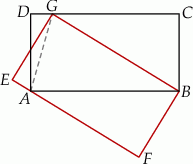
Dany jest równoległobok 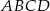 . Na przedłużeniu przekątnej
. Na przedłużeniu przekątnej 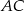 wybrano punkt
wybrano punkt 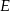 tak, że
tak, że 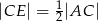 (zobacz rysunek). Uzasadnij, że pole równoległoboku
(zobacz rysunek). Uzasadnij, że pole równoległoboku 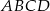 jest cztery razy większe od pola trójkąta
jest cztery razy większe od pola trójkąta 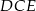 .
.
Na przekątnej  równoległoboku
równoległoboku  wybrano punkt
wybrano punkt 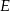 (zobacz rysunek). Uzasadnij, że trójkąty
(zobacz rysunek). Uzasadnij, że trójkąty 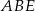 i
i 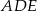 mają równe pola.
mają równe pola.