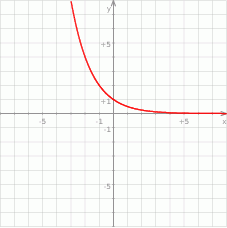
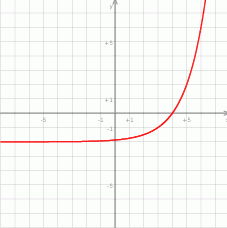
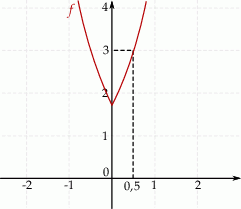
Na rysunku narysowano fragment wykresu funkcji 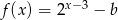 , określonej dla
, określonej dla 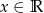 .
.
- Podaj wartość
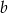 .
. - Naszkicuj wykres funkcji
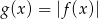 .
. - Podaj wszystkie wartości parametru
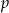 , dla których równanie
, dla których równanie 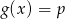 ma dokładnie jedno rozwiązanie.
ma dokładnie jedno rozwiązanie.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku narysowano fragment wykresu funkcji 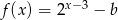 , określonej dla
, określonej dla 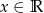 .
.
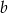 .
. 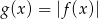 .
. 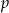 , dla których równanie
, dla których równanie 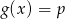 ma dokładnie jedno rozwiązanie.
ma dokładnie jedno rozwiązanie.
Wykres funkcji wykładniczej 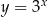 przekształcono i otrzymano wykres funkcji
przekształcono i otrzymano wykres funkcji 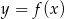 (rys).
(rys).
Napisz wzór funkcji 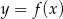 , a następnie zaznacz na płaszczyźnie zbiór
, a następnie zaznacz na płaszczyźnie zbiór
![{ } A = x,y : x ∈ R i y ∈ R i log(x−1)2+y 2[log 9f2(x)] < 0 .](https://img.zadania.info/zad/2686807/HzadT4x.gif)
Na rysunku przedstawiony jest wykres funkcji wykładniczej 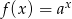 dla
dla 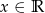 .
.
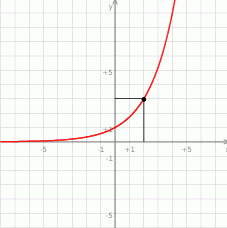
 .
. 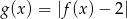 i podaj wszystkie wartości parametru
i podaj wszystkie wartości parametru 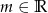 , dla których równanie
, dla których równanie 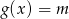 ma dokładnie jedno rozwiązanie.
ma dokładnie jedno rozwiązanie.Naszkicuj wykres funkcji 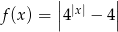 . Na podstawie wykresu określ przedziały, w których funkcja jest rosnącą.
. Na podstawie wykresu określ przedziały, w których funkcja jest rosnącą.
Narysuj wykres funkcji 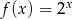 , a następnie narysuj wykres funkcji
, a następnie narysuj wykres funkcji 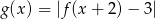 .
.
Na rysunku przedstawiono fragment wykresu funkcji wykładniczej określonej wzorem 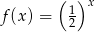 . Rozważamy funkcję
. Rozważamy funkcję 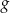 określoną wzorem
określoną wzorem 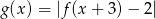 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 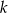 , dla których równanie
, dla których równanie 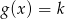 ma dwa rozwiązania takie, że ich iloczyn jest liczbą ujemną.
ma dwa rozwiązania takie, że ich iloczyn jest liczbą ujemną.