Objętość metalowej kuli jest równa 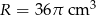 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Objętość tej kuli jest większa niż 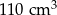 . . | P | F |
Pole powierzchni tej kuli jest równe 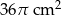 . . | P | F |
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Objętość metalowej kuli jest równa 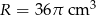 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Objętość tej kuli jest większa niż 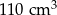 . . | P | F |
Pole powierzchni tej kuli jest równe 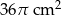 . . | P | F |
Rozważmy treść następującego zadania:
Obwód prostokąta o bokach długości  i
i 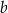 jest równy 60. Jeden z boków tego prostokąta jest o 10 dłuższy od drugiego. Oblicz długości boków tego prostokąta.
jest równy 60. Jeden z boków tego prostokąta jest o 10 dłuższy od drugiego. Oblicz długości boków tego prostokąta.
Który układ równań opisuje zależności między długościami boków tego prostokąta?
A) 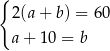 B)
B) 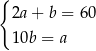 C)
C) 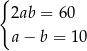 D)
D) 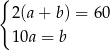
Rozważmy treść następującego zadania:
Pole prostokąta o bokach długości  i
i 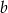 jest równe 40. Jeden z boków tego prostokąta jest o 15 krótszy od drugiego. Oblicz długości boków tego prostokąta.
jest równe 40. Jeden z boków tego prostokąta jest o 15 krótszy od drugiego. Oblicz długości boków tego prostokąta.
Który układ równań opisuje zależności między długościami boków tego prostokąta?
A) 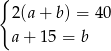 B)
B) 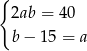 C)
C) 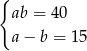 D)
D) 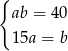
Mediana danych przedstawionych w tabeli liczebności jest równa
| Wartość | 0 | 1 | 2 | 3 |
| Liczebność | 5 | 2 | 1 | 1 |
A) 0 B) 0,5 C) 1 D) 5
W tabeli poniżej przedstawione są wyniki pracy klasowej.
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba uczniów | 2 | 3 | 7 | 6 | 4 | 2 |
Mediana ocen w tej klasie jest równa
A) 3,5 B) 3 C) 4 D) 4,5
Rzucając wielokrotnie symetryczną kostką do gry otrzymano następujące liczby oczek
| Liczba oczek | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba wyników | 2 | 4 | 3 | 4 | 5 | 3 |
Mediana tych danych jest równa.
A) 3 B) 3,5 C) 4 D) 5
W pewnej grupie uczniów przeprowadzono ankietę na temat liczby odsłuchanych audiobooków w lutym 2022 roku. Wyniki ankiety przedstawiono w tabeli.
| Liczba odsłuchanych audiobooków | 0 | 1 | 2 | 3 | 4 | 7 |
| Liczba uczniów | 9 | 5 | 3 | 4 | 1 | 3 |
Mediana liczby odsłuchanych audiobooków w tej grupie uczniów jest równa
A) 3 B) 2 C) 1 D) 
Mediana danych przedstawionych w tabeli liczebności jest równa
| Wartość | 0 | 1 | 2 | 3 |
| Liczebność | 4 | 3 | 2 | 5 |
A) 2 B) 1,5 C) 1 D) 0,5
Rzucając wielokrotnie symetryczną kostką do gry otrzymano następujące liczby oczek
| Liczba oczek | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba wyników | 4 | 3 | 3 | 4 | 2 | 3 |
Mediana tych danych jest równa.
A) 3 B) 3,5 C) 4 D) 5
Abiturient jednego z liceów zestawił w tabeli oceny ze swojego świadectwa ukończenia szkoły.
| Ocena | 6 | 5 | 4 | 3 | 2 |
| Liczba ocen | 2 | 3 | 5 | 5 | 1 |
Mediana przedstawionego zestawu danych jest równa
A) 3 B) 3,5 C) 4 D) 4,5
W tabeli poniżej przedstawione są wyniki pracy klasowej.
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba ocen | 2 | 5 | 2 | 12 | 5 | 1 |
Mediana ocen w tej klasie jest równa
A) 3 B) 3,5 C) 4 D) 5
Na ulicznym straganie z kwiatami sprzedano tyle samo róż, co tulipanów oraz 16 goździków. Goździki stanowiły 12,5% liczby sprzedanych kwiatów. Ile tulipanów sprzedano na straganie?
A) 56 B) 28 C) 64 D) 112
Adam przygotował karty do gry z czterech arkuszy kartonu. Najpierw podzielił każdy arkusz kartonu na cztery części, a następnie każdą z nich ponownie podzielił na cztery części. Tak powstał komplet kart. W grze bierze udział 5 graczy, z których każdy otrzymuje jednakową liczbę kart. Adam przygotował A/B karty do gry.
A) 32 B) 64
Każdy gracz może otrzymać maksymalnie C/D kart.
C) 12 D) 13
Oskar przygotował karty do gry z trzech arkuszy kartonu. Najpierw podzielił każdy arkusz kartonu na sześć części, a następnie każdą z nich ponownie podzielił na sześć części. Tak powstał komplet kart. W grze bierze udział 5 graczy, z których każdy otrzymuje jednakową liczbę kart. Oskar przygotował A/B kart(y) do gry.
A) 108 B) 144
Każdy gracz może otrzymać maksymalnie C/D kart(y).
C) 22 D) 21
Z czarnych krążków układane są figury w kształcie kwadratu, według reguły przedstawionej na rysunku.
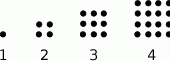
O ile więcej krążków będzie w figurze numer 12 niż w figurze numer 10?
A) 144 B) 44 C) 42 D) 40
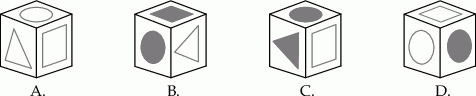
Na kartonowej siatce sześcianu Mariusz nakleił 6 figur tak, jak pokazano na rysunku. Następnie z tej siatki skleił kostkę.
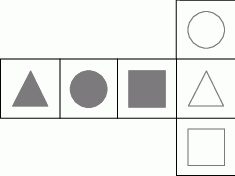
Który rysunek przedstawia kostkę sklejoną przez Mariusza?
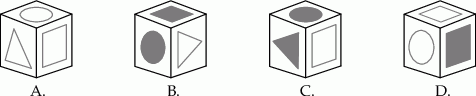
Na kartonowej siatce sześcianu Mariusz nakleił 6 figur tak, jak pokazano na rysunku. Następnie z tej siatki skleił kostkę.
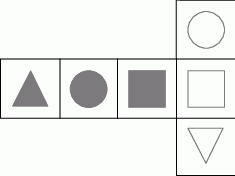
Który rysunek przedstawia kostkę sklejoną przez Mariusza?
W równoległoboku 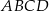 kąt przy wierzchołku
kąt przy wierzchołku 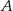 ma większą miarę, niż kąt przy wierzchołku
ma większą miarę, niż kąt przy wierzchołku 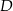 . Suma miar pewnych trzech kątów tego równoległoboku jest równa
. Suma miar pewnych trzech kątów tego równoległoboku jest równa 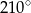 .
.
Miara kąta przy wierzchołku 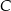 równoległoboku jest równa A/B.
równoległoboku jest równa A/B.
A) 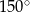 B)
B) 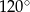
Miara kąta przy wierzchołku 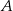 jest C/D razy większa od miary kąta przy wierzchołku
jest C/D razy większa od miary kąta przy wierzchołku 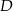 .
.
C) 4 D) 5
Pole prostokąta wynosi 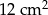 . Pole prostokąta do niego podobnego jest równe
. Pole prostokąta do niego podobnego jest równe 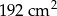 . Skala podobieństwa prostokąta mniejszego do większego jest równa
. Skala podobieństwa prostokąta mniejszego do większego jest równa
A) 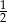 B)
B)  C)
C) 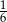 D)
D) 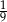
Julia połowę swoich oszczędności przeznaczyła na prezent dla Maćka. 10% tego, co jej zostało, przeznaczyła na prezent dla Dominiki. Ile procent oszczędności pozostało Julii?
A) 25 B) 40 C) 45 D) 55
Wojtek 40% swoich oszczędności przeznaczył na zakup nowego plecaka. Połowę z tego, co mu zostało, przeznaczył na zakup butów. Ile procent oszczędności pozostało Wojtkowi?
A) 10% B) 30% C) 40% D) 20%
Czworokąt 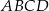 jest deltoidem, w którym dłuższa przekątna
jest deltoidem, w którym dłuższa przekątna 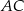 ma taką samą długość jak ramiona
ma taką samą długość jak ramiona 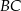 i
i 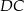 , a kąt
, a kąt 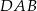 ma miarę
ma miarę 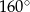 .
.
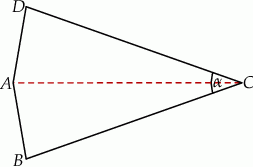
Miara kąta 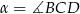 jest równa
jest równa
A) 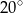 B)
B) 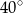 C)
C) 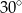 D)
D) 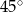
Po dodaniu do zestawu liczb: 10, 4, 5, 9, 12 jednej liczby średnia liczb zmniejszyła się o 1.
Którą z poniższych liczb dopisano?
A) 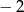 B)
B) 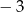 C) 2 D) 3
C) 2 D) 3
Dany jest zestaw liczb: 4, 9, 11, 15, 21. Do podanych liczb dopisano jeszcze jedną liczbę i wtedy średnia arytmetyczna nowego zestawu liczb zwiększyła się o 1. Która liczba została dopisana?
A) 10 B) 12 C) 13 D) 18
Po usunięciu z zestawu liczb: 15, 10, 4, 5, 9, 12, 8 jednej liczby średnia liczb nie zmieniła się.
Którą z poniższych liczb usunięto?
A) 8 B) 9 C) 10 D) 12
Zbiornik z cementem jest opróżniany na znajdujący się pod nim taśmociąg. Na wykresie przedstawiono ilość cementu pozostałego w zbiorniku w zależności od czasu upływającego od momentu rozpoczęcia opróżniania zbiornika.
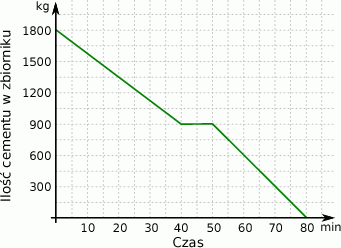
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Na 10 minut przed zakończeniem opróżniania zbiornika wciąż było w nim 300 kg cementu. | P | F |
| W trakcie pierwszych dwudziestu minut opróżniania zbiornika wysypano z niego 1350 kg cementu. | P | F |
Zbiornik z cementem jest opróżniany na znajdujący się pod nim taśmociąg. Na wykresie przedstawiono ilość cementu pozostałego w zbiorniku w zależności od czasu upływającego od momentu rozpoczęcia opróżniania zbiornika.
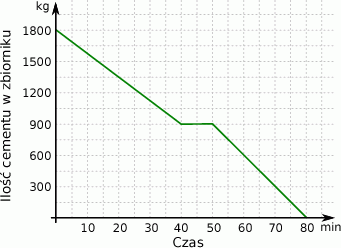
Średnia prędkość z jaką opróżniono pierwszą połowę zawartości zbiornika wyniosła
A) 1350 kg/h B) 800 kg/h C) 2250 kg/h D) 1080 kg/h
Czterech przyjaciół zarejestrowało spółkę. Wysokość udziałów poszczególnych wspólników w kapitale zakładowym spółki wyraża stosunek 12 : 8 : 3 : 2. Jaką część kapitału zakładowego stanowi udział największego inwestora?
A) 12% B) 32% C) 48% D) 52%
Czterech przyjaciół zarejestrowało spółkę. Wysokość udziałów poszczególnych wspólników w kapitale zakładowym spółki wyraża stosunek 12 : 8 : 3 : 2. Jaką część kapitału zakładowego stanowi udział najmniejszego inwestora?
A) 2% B) 4% C) 6% D) 8%
Pan Józef odbył podróż pomiędzy czterema miastami: najpierw samolotem pomiędzy miastami 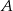 i
i 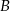 , później samochodem pomiędzy miastami
, później samochodem pomiędzy miastami  i
i 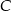 , potem pociągiem między miastami
, potem pociągiem między miastami 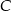 i
i 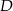 , a na koniec wrócił autokarem do miasta
, a na koniec wrócił autokarem do miasta 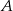 . Na rysunku przedstawiono schemat tej podróży.
. Na rysunku przedstawiono schemat tej podróży.
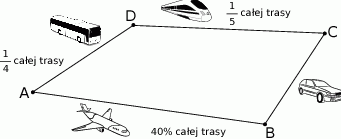
Droga przebyta samochodem stanowiła mniej niż 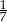 całej trasy podróży. całej trasy podróży. | P | F |
| Dystans pokonany samolotem był dwa razy większy od dystansu pokonanego pociągiem. | P | F |
Pan Józef odbył podróż pomiędzy czterema miastami: najpierw samolotem pomiędzy miastami 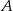 i
i 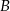 , później samochodem pomiędzy miastami
, później samochodem pomiędzy miastami 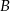 i
i 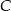 , potem pociągiem między miastami
, potem pociągiem między miastami 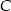 i
i 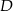 , a na koniec wrócił autokarem do miasta
, a na koniec wrócił autokarem do miasta 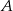 . Na rysunku przedstawiono schemat tej podróży.
. Na rysunku przedstawiono schemat tej podróży.
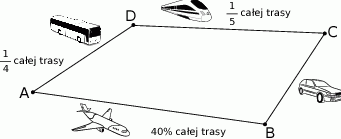
Rzucamy raz symetryczną sześcienną kostką do gry. Jakie jest prawdopodobieństwo, że w rzucie tą kostką wypadnie liczba oczek większa od 2, ale mniejsza od 6?
A) 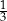 B)
B) 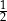 C)
C)  D)
D) 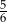
Kula wpisana w sześcian o przekątnej równej 6 ma objętość równą
A) 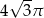 B)
B) 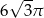 C)
C) 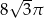 D)
D) 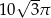
Jedną ścianę drewnianego sześcianu pomalowano na czerwono, a pozostałe – na biało. Ten sześcian rozcięto na 27 jednakowych sześcianów. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Tylko cztery małe sześciany mają dokładnie jedną ścianę pomalowaną na biało. | P | F |
| Tylko cztery małe sześciany mają trzy ściany pomalowane na biało. | P | F |
Dwie przeciwległe ściany drewnianego sześcianu pomalowano na czerwono, a pozostałe – na biało. Ten sześcian rozcięto na 27 jednakowych sześcianów. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Sześć małych sześcianów ma dokładnie jedną ścianę pomalowaną farbą. | P | F |
| Tylko cztery małe sześciany mają jedną ścianę pomalowaną na biało. | P | F |
Pole kwadratu 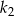 jest o 21% większe od pola kwadratu
jest o 21% większe od pola kwadratu 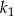 . Wówczas długość boku kwadratu
. Wówczas długość boku kwadratu 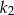 jest większa od długości boku kwadratu
jest większa od długości boku kwadratu 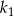 o
o
A) 10% B) 110% C) 21% D) 121%
Na rysunku przedstawiono równoległobok 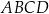 , który nie jest prostokątem. Długości boków tego równoległoboku opisano za pomocą wyrażeń algebraicznych.
, który nie jest prostokątem. Długości boków tego równoległoboku opisano za pomocą wyrażeń algebraicznych.
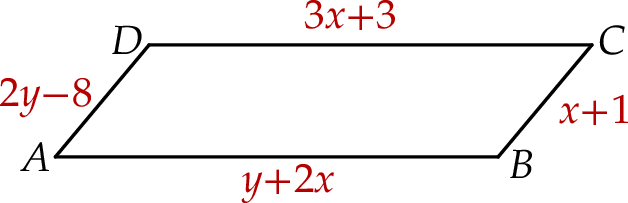
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole równoległoboku 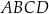 jest równe 48. jest równe 48. | P | F |
Obwód równoległoboku 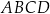 jest równy 32. jest równy 32. | P | F |
