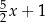Jeden bok kwadratu o polu 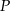 zmniejszono o 30% a drugi zwiększono o 30%. Pole powstałego w ten sposób prostokąta jest równe
zmniejszono o 30% a drugi zwiększono o 30%. Pole powstałego w ten sposób prostokąta jest równe
A) 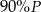 B)
B) 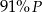 C)
C) 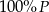 D)
D) 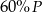
/Szkoła podstawowa/Zadania testowe
Jeden bok kwadratu wydłużono o 10%, a drugi bok skrócono o 10% w taki sposób, że otrzymano prostokąt. Pole tego prostokąta jest
A) równe polu kwadratu
B) mniejsze od pola kwadratu o 10%
C) większe od pola kwadratu o 10%
D) mniejsze od pola kwadratu o 1%
Dane są liczby  i
i 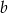 takie, że
takie, że 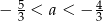 oraz
oraz 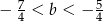 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Iloraz 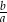 jest zawsze dodatni. jest zawsze dodatni. | P | F |
Różnica 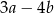 jest zawsze dodatnia. jest zawsze dodatnia. | P | F |
W układzie współrzędnych narysowano sześciokąt foremny o boku 2 tak, że jednym z jego wierzchołków jest punkt 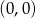 , a jeden z jego boków leży na osi
, a jeden z jego boków leży na osi  . Do tego sześciokąta dorysowujemy kolejne takie same sześciokąty. Umieszczamy je tak, jak na rysunku, aby każdy następny sześciokąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego sześciokąta leżał na osi
. Do tego sześciokąta dorysowujemy kolejne takie same sześciokąty. Umieszczamy je tak, jak na rysunku, aby każdy następny sześciokąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego sześciokąta leżał na osi  . Poniżej przedstawiono dorysowane, zgodnie z tą regułą, sześciokąty, które ponumerowano kolejnymi liczbami naturalnymi.
. Poniżej przedstawiono dorysowane, zgodnie z tą regułą, sześciokąty, które ponumerowano kolejnymi liczbami naturalnymi.
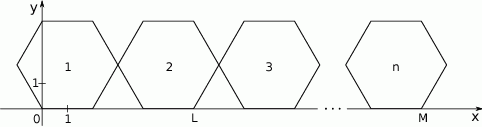
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pierwsza współrzędna wierzchołka 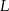 w drugim sześciokącie jest równa 6. w drugim sześciokącie jest równa 6. | P | F |
Pierwsza współrzędna wierzchołka 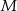 w w  –tym sześciokącie jest równa –tym sześciokącie jest równa 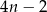 . . | P | F |
W układzie współrzędnych narysowano trójkąt równoboczny tak, że jednym z jego wierzchołków jest punkt 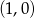 , jeden z wierzchołków jest na osi
, jeden z wierzchołków jest na osi 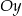 , a jeden z jego boków jest równoległy do osi
, a jeden z jego boków jest równoległy do osi 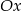 . Do tego trójkąta dorysowujemy kolejne takie same trójkąty. Umieszczamy je tak, jak na rysunku, aby każdy następny trójkąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego trójkąta był równoległy do osi
. Do tego trójkąta dorysowujemy kolejne takie same trójkąty. Umieszczamy je tak, jak na rysunku, aby każdy następny trójkąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego trójkąta był równoległy do osi 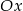 . Poniżej przedstawiono dorysowane, zgodnie z tą regułą, trójkąty, które ponumerowano kolejnymi liczbami naturalnymi.
. Poniżej przedstawiono dorysowane, zgodnie z tą regułą, trójkąty, które ponumerowano kolejnymi liczbami naturalnymi.
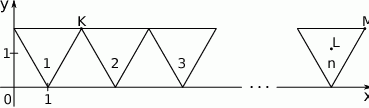
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Środek 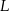 w w  –tym trójkącie ma współrzędne –tym trójkącie ma współrzędne 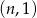 . . | P | F |
Wierzchołek 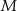 w w  –tym trójkącie ma współrzędne –tym trójkącie ma współrzędne 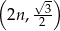 . . | P | F |
W układzie współrzędnych narysowano kwadrat o przekątnej długości 4 tak, że jednym z jego wierzchołków jest punkt 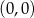 , a jedna z jego przekątnych jest równoległa do osi
, a jedna z jego przekątnych jest równoległa do osi 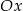 . Do tego kwadratu dorysowujemy kolejne takie same kwadraty. Umieszczamy je tak, jak na rysunku, aby każdy następny kwadrat miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jedna z przekątnych każdego kwadratu była równoległa do osi
. Do tego kwadratu dorysowujemy kolejne takie same kwadraty. Umieszczamy je tak, jak na rysunku, aby każdy następny kwadrat miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jedna z przekątnych każdego kwadratu była równoległa do osi 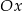 . Poniżej przedstawiono dorysowane, zgodnie z tą regułą, kwadraty, które ponumerowano kolejnymi liczbami naturalnymi.
. Poniżej przedstawiono dorysowane, zgodnie z tą regułą, kwadraty, które ponumerowano kolejnymi liczbami naturalnymi.
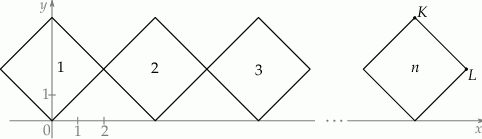
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pierwsza współrzędna wierzchołka 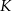 w w  –tym kwadracie jest równa –tym kwadracie jest równa 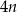 . . | P | F |
Pierwsza współrzędna wierzchołka 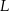 w w  –tym kwadracie jest równa –tym kwadracie jest równa 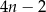 . . | P | F |
O liczbie  wiemy, że
wiemy, że 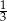 tej liczby jest o
tej liczby jest o  większa od
większa od  tej liczby. Które równanie pozwoli wyznaczyć liczbę
tej liczby. Które równanie pozwoli wyznaczyć liczbę  ?
?
A) 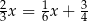 B)
B) 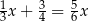 C)
C) 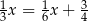 D)
D) 
O liczbie  wiemy, że
wiemy, że 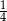 tej liczby jest o
tej liczby jest o  mniejsza od
mniejsza od 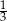 tej liczby. Które równanie pozwoli wyznaczyć liczbę
tej liczby. Które równanie pozwoli wyznaczyć liczbę  ?
?
A) 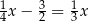 B)
B) 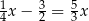 C)
C) 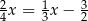 D)
D) 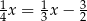
Która z poniższych liczb jest większa od 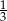 ?
?
A) 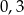 B)
B) 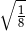 C)
C) 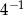 D)
D) 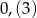
Która z poniższych liczb jest większa od  ?
?
A) 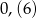 B)
B) 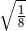 C)
C) 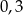 D)
D) 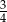
Która z poniższych liczb jest większa od 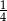 ?
?
A) 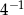 B)
B) 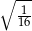 C)
C) 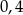 D)
D) 
Adam zapisał, w przypadkowej kolejności, podane w programie radiowym wartości temperatury odnotowane pewnego zimowego dnia o godzinie 20:30 w Zakopanem, w Wiśle, w Karpaczu i w Szklarskiej Porębie (zobacz rysunek).
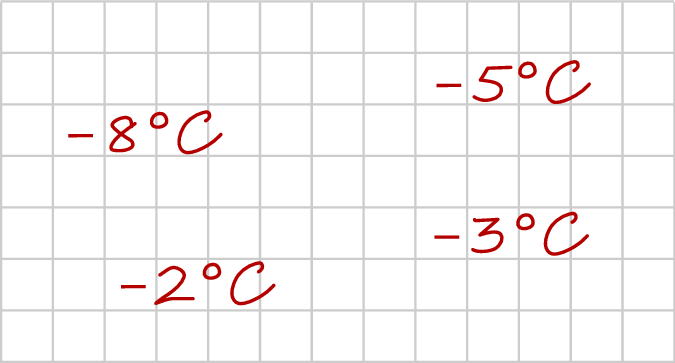
Temperatura w Karpaczu była o 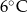 wyższa niż w Szklarskiej Porębie, a w Wiśle była niższa niż w Zakopanem. Temperaturę
wyższa niż w Szklarskiej Porębie, a w Wiśle była niższa niż w Zakopanem. Temperaturę 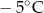 zanotowano w
zanotowano w
A) Szklarskiej Porębie. B) Zakopanem. C) Karpaczu. D) Wiśle.
Rozwiązaniem układu równań 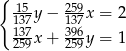 jest para liczb
jest para liczb
A) 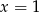 i
i 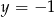 B)
B) 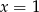 i
i 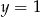 C)
C) 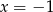 i
i 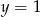 D)
D) 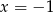 i
i 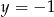
Na rysunku przedstawiono czworokąt 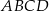 , w którym
, w którym 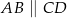 i trójkąt równoramienny
i trójkąt równoramienny 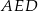 , w którym
, w którym 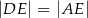 . Miara kąta
. Miara kąta 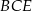 jest równa
jest równa 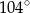 , a miara kąta
, a miara kąta 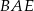 jest równa
jest równa 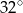 .
.
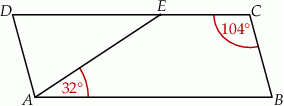
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt 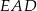 ma miarę ma miarę 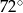 . . | P | F |
Czworokąt  jest równoległobokiem. jest równoległobokiem. | P | F |
Korzystając z tego, że 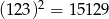 , wskaż wartość liczby
, wskaż wartość liczby 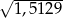 .
.
A) 0,0123 B) 0,123 C) 1,23 D) 12,3
Korzystając z tego, że 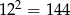 , wskaż wartość liczby
, wskaż wartość liczby 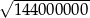 .
.
A) 120 000 B) 12 000 C) 1 200 D) 1 200 000
Bilet ulgowy do cyrku jest o 40% tańszy od biletu normalnego. Tata Jacka za 2 bilety normalne i 3 ulgowe zapłacił 228 zł.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Mama Patrycji za 1 bilet normalny i 2 ulgowe musi zapłacić 132 zł. | P | F |
| Bilet normalny jest droższy od ulgowego o 26 zł. | P | F |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba 3069792 jest liczbą podzielną przez 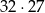 . . | P | F |
Liczba 3069792 nie jest podzielna przez 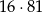 . . | P | F |
Liczba przeciwna do podwojonej odwrotności liczby  jest równa
jest równa
A) 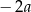 B)
B) 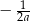 C)
C) 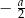 D)
D) 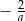
Liczba odwrotna do podwojonej odwrotności liczby  jest równa
jest równa
A) 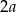 B)
B) 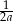 C)
C) 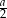 D)
D) 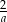
Liczba przeciwna do potrojonej odwrotności liczby  jest równa
jest równa
A) 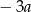 B)
B) 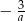 C)
C) 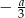 D)
D) 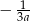
Jabłka w trakcie suszenia straciły 40% swojej masy i po wysuszeniu ważą 1,5 kg. Jabłka przed wysuszeniem ważyły
A) 3,3 kg B) 2,5 kg C) 3 kg D) 2,1 kg
Do 2 kg roztworu soli dolano 0,25 litra wody i stężenie procentowe roztworu zmniejszyło się o 1 punkt procentowy. Jakie jest stężenie procentowe otrzymanego roztworu?
A) 8% B) 5% C) 9% D) 6%
Do 1,6 kg roztworu soli dolano 0,9 litra wody i stężenie procentowe roztworu zmniejszyło się o 4,5 punktu procentowego. Jakie jest stężenie procentowe otrzymanego roztworu?
A) 8% B) 5% C) 9% D) 6%
Dane są cztery liczby: 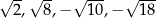 . Suma trzech spośród nich jest równa 0. Którą liczbę należy odrzucić, aby suma pozostałych trzech liczb była równa 0?
. Suma trzech spośród nich jest równa 0. Którą liczbę należy odrzucić, aby suma pozostałych trzech liczb była równa 0?
A) 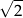 B)
B) 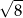 C)
C) 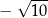 D)
D) 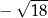
Na wycieczkę szkolną początkowo miało pojechać  chłopców i
chłopców i 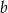 dziewczynek z klasy 5A oraz
dziewczynek z klasy 5A oraz  chłopców i
chłopców i 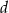 dziewczynek z klasy 6A. Ostatecznie jednak z wycieczki zrezygnowało 10% chłopców z klasy 5A oraz 6 dziewczynek z klasy 6A. Dodatkowo do wycieczki dołączyło 4 chłopców z klasy 6A i 1 dziewczynka z klasy 5A. Liczba uczniów klas 5A i 6A, którzy pojechali na wycieczkę jest równa
dziewczynek z klasy 6A. Ostatecznie jednak z wycieczki zrezygnowało 10% chłopców z klasy 5A oraz 6 dziewczynek z klasy 6A. Dodatkowo do wycieczki dołączyło 4 chłopców z klasy 6A i 1 dziewczynka z klasy 5A. Liczba uczniów klas 5A i 6A, którzy pojechali na wycieczkę jest równa
A) 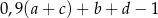 B)
B) 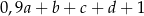
C) 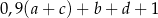 D)
D) 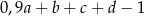
W trapezie 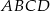 punkt
punkt 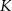 jest środkiem ramienia
jest środkiem ramienia 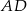 , a punkt
, a punkt 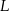 jest środkiem podstawy
jest środkiem podstawy 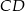 .
.
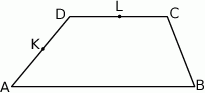
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Trójkąt 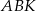 ma takie samo pole, jak trójkąt ma takie samo pole, jak trójkąt 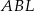 . . | P | F |
Pole trójkąta 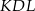 jest dwa razy mniejsze od pola trójkąta jest dwa razy mniejsze od pola trójkąta 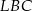 . . | P | F |
Trzy koleżanki kupiły bilety autobusowe w tym samym automacie. Martyna kupiła 6 biletów 75–minutowych i zapłaciła za te bilety 24 zł. Weronika kupiła 4 bilety 20–minutowe i zapłaciła za nie 12 zł. Ania kupiła 2 bilety 75–minutowe i 2 bilety 20–minutowe. Ile Ania zapłaciła za bilety?
A) 7 zł B) 14 zł C) 19 zł D) 20 zł
Trzech kolegów kupiło bilety autobusowe w tym samym automacie. Wiktor kupił 8 biletów 75–minutowych i zapłacił za te bilety 36 zł. Jacek kupił 6 biletów 20–minutowych i zapłacił za nie 15 zł. Przemek kupił 7 biletów 75–minutowych i 7 biletów 20–minutowych. Ile Przemek zapłacił za bilety?
A) 49 zł B) 51 zł C) 42 zł D) 56 zł
Na osi liczbowej zaznaczono dwa punkty 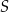 i
i 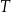 . Odcinek
. Odcinek 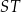 podzielono na 12 równych części.
podzielono na 12 równych części.

Długość odcinka 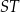 jest równa
jest równa
A) 1750 B) 1500 C) 1250 D) 1000
Na osi liczbowej zaznaczono punkty 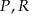 i
i 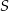 oraz podano współrzędne punktów
oraz podano współrzędne punktów 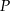 i
i 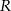 . Odcinek
. Odcinek 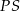 jest podzielony na 8 równych części (zobacz rysunek poniżej).
jest podzielony na 8 równych części (zobacz rysunek poniżej).
![]()
Współrzędna punktu 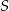 jest równa
jest równa
A) 10 B) 11 C) 13 D) 15
Na osi liczbowej zaznaczono punkty 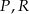 i
i 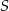 oraz podano współrzędne punktów
oraz podano współrzędne punktów 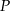 i
i 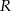 . Odcinek
. Odcinek 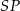 jest podzielony na 8 równych części (zobacz rysunek poniżej).
jest podzielony na 8 równych części (zobacz rysunek poniżej).
![]()
Współrzędna punktu 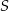 jest równa
jest równa
A) 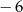 B)
B) 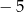 C)
C) 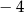 D)
D) 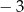
Połowę liczby  zmniejszono o 3, a następnie do otrzymanego wyniku dodano dwukrotność liczby
zmniejszono o 3, a następnie do otrzymanego wyniku dodano dwukrotność liczby 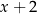 . W wyniku tych działań otrzymano wyrażenie
. W wyniku tych działań otrzymano wyrażenie
A) 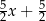 B)
B) 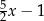 C)
C) 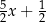 D)
D)