Do pięciu różnych naczyń rozlano 6 litrów wody.
Średnia arytmetyczna ilości wody w tych naczyniach zmieni się, gdy
A) jedno naczynie opróżnimy, przelewając jego zawartość do pozostałych naczyń.
B) poprzelewamy wodę z jednego naczynia do drugiego, tak by w każdym naczyniu było jej tyle samo.
C) z czterech naczyń odlejemy trochę wody do piątego naczynia.
D) do każdego naczynia dolejemy taką samą ilość wody.
/Szkoła podstawowa/Zadania testowe
Dane są kula o środku w punkcie 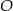 i promieniu
i promieniu  oraz walec o promieniu podstawy
oraz walec o promieniu podstawy  i wysokości
i wysokości  .
.
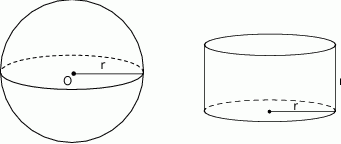
Na podstawie informacji wybierz zdanie prawdziwe.
A) Objętość kuli jest równa objętości walca.
B) Objętość kuli jest 2 razy większa od objętości walca.
C) Objętość walca stanowi  objętości kuli.
objętości kuli.
D) Objętość walca jest 3 razy mniejsza od objętości kuli.
Dane są kula o środku w punkcie 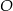 i promieniu
i promieniu  oraz walec o promieniu podstawy
oraz walec o promieniu podstawy  i wysokości
i wysokości 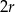 .
.
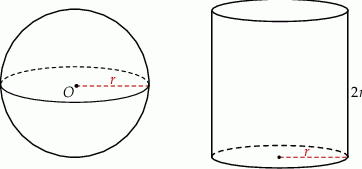
A) Objętość kuli jest równa objętości walca.
B) Objętość walca stanowi  objętości kuli.
objętości kuli.
C) Objętość kuli jest 2 razy mniejsza od objętości walca.
D) Objętość walca stanowi  objętości kuli.
objętości kuli.
W X edycji konkursu recytatorskiego wzięło udział 140 dziewcząt i 112 chłopców. W XI edycji tego konkursu wzięła udział ta sama liczba osób, ale liczba dziewcząt zmalała o 20%.
Liczba chłopców w XI edycji konkursu wzrosła w stosunku do liczby chłopców w X edycji o
A) 25% B) 12,5% C) 40% D) 20%
W X edycji konkursu recytatorskiego wzięło udział 140 dziewcząt i 112 chłopców. W XI edycji tego konkursu wzięła udział ta sama liczba osób, ale liczba dziewcząt zmalała o 20%. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W X edycji konkursu wzięło udział o 20% dziewcząt więcej niż w XI edycji. | P | F |
| Liczba chłopców w XI edycji konkursu wzrosła w stosunku do liczby chłopców w X edycji o 20%. | P | F |
Czy kulę o objętości 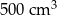 można przełożyć przez otwór w kształcie kwadratu o boku 10 cm? Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród oznaczonych literami A–D.
można przełożyć przez otwór w kształcie kwadratu o boku 10 cm? Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród oznaczonych literami A–D.
| Tak | Nie |
| ponieważ | |
| A) | średnica kuli jest mniejsza od przekątnej kwadratu. |
| B) | średnica kuli jest mniejsza od boku kwadratu. |
| C) | średnica kuli jest większa od przekątnej kwadratu. |
| D) | średnica kuli jest większa od boku kwadratu. |
Czy kulę o objętości 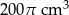 można przełożyć przez otwór w kształcie kwadratu o boku 10 cm? Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród oznaczonych literami A–D.
można przełożyć przez otwór w kształcie kwadratu o boku 10 cm? Wybierz odpowiedź T (tak) albo N (nie) i jej uzasadnienie spośród oznaczonych literami A–D.
| Tak | Nie |
| ponieważ | |
| A) | średnica kuli jest mniejsza od przekątnej kwadratu. |
| B) | średnica kuli jest mniejsza od boku kwadratu. |
| C) | średnica kuli jest większa od przekątnej kwadratu. |
| D) | średnica kuli jest większa od boku kwadratu. |
Na rysunku poniżej przedstawiono siatkę sześcianu. Punkty: 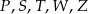 są środkami jego krawędzi.
są środkami jego krawędzi.
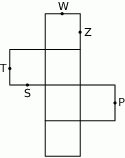
Po złożeniu sześcianu z tej siatki punkt 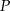 pokryje się z punktem
pokryje się z punktem
A) 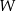 B)
B) 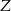 C)
C) 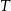 D)
D) 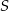
Na rysunku poniżej przedstawiono siatkę sześcianu. Punkty: 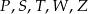 są środkami jego krawędzi.
są środkami jego krawędzi.
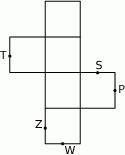
Po złożeniu sześcianu z tej siatki punkt 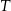 pokryje się z punktem
pokryje się z punktem
A) 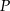 B)
B) 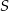 C)
C) 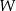 D)
D) 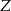
Maciek rysuje siatkę ostrosłupa prawidłowego, którego podstawą jest kwadrat o środku w punkcie 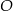 i boku długości 8.
i boku długości 8.
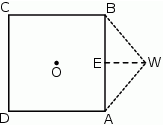
Czy trójkąt 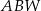 o bokach długości odpowiednio: 8, 5, 5 może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
o bokach długości odpowiednio: 8, 5, 5 może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
| Tak | Nie |
| ponieważ | |
| A) | trójkąt 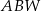 jest równoramienny. jest równoramienny. |
| B) | odległość 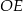 jest mniejsza niż wysokość jest mniejsza niż wysokość 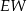 trójkąta trójkąta 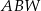 . . |
| C) | odległość 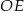 jest większa niż wysokość jest większa niż wysokość 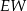 trójkąta trójkąta 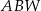 . . |
Hela rysuje siatkę ostrosłupa, którego podstawą jest prostokątny trójkąt równoramienny 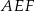 .
.
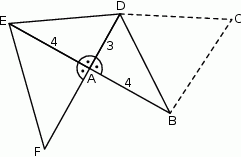
Czy trójkąt równoboczny 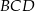 może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
| Tak | Nie |
| ponieważ | |
| A) | odcinki 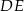 i i 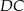 mają różne długości. mają różne długości. |
| B) | odcinki 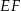 i i 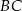 mają różne długości. mają różne długości. |
| C) | odcinki 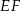 i i 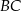 mają równe długości. mają równe długości. |
Maciek rysuje siatkę ostrosłupa prawidłowego, którego podstawą jest kwadrat o środku w punkcie 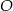 i boku długości 6.
i boku długości 6.
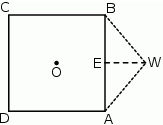
Czy trójkąt 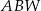 o bokach długości odpowiednio: 6, 5, 5 może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
o bokach długości odpowiednio: 6, 5, 5 może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
| Tak | Nie |
| ponieważ | |
| A) | trójkąt 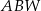 jest równoramienny. jest równoramienny. |
| B) | odległość 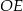 jest mniejsza niż wysokość jest mniejsza niż wysokość 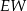 trójkąta trójkąta 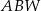 . . |
| C) | odległość 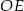 jest większa niż wysokość jest większa niż wysokość 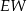 trójkąta trójkąta 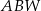 . . |
Które zdanie jest fałszywe?
A) Jeżeli iloczyn liczb  i
i 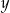 jest dodatni, to liczby te mają taki sam znak.
jest dodatni, to liczby te mają taki sam znak.
B) Jeżeli iloczyn liczb  i
i 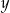 jest równy zero to liczby te są równe zero.
jest równy zero to liczby te są równe zero.
C) Jeżeli iloczyn liczb  i
i 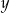 jest ujemny to liczby te mają różne znaki.
jest ujemny to liczby te mają różne znaki.
D) Jeżeli suma liczb  i
i 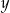 jest równa zero to ich iloczyn jest niedodatni.
jest równa zero to ich iloczyn jest niedodatni.
Do przedziału 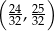 należy liczba
należy liczba
A) 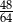 B)
B) 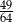 C)
C) 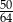 D)
D) 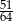
Do przedziału 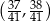 należy liczba
należy liczba
A) 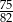 B)
B) 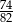 C)
C) 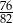 D)
D) 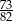
Do przedziału 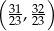 należy liczba
należy liczba
A) 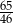 B)
B)  C)
C) 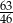 D)
D) 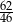
Na rysunku przedstawiono trapez 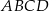 zbudowany z dwóch równoramiennych trójkątów prostokątnych. Krótsza przekątna tego trapezu ma długość 10 cm.
zbudowany z dwóch równoramiennych trójkątów prostokątnych. Krótsza przekątna tego trapezu ma długość 10 cm.
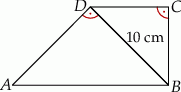
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Obwód trapezu 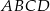 jest równy jest równy 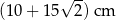 . . | P | F |
Pole trapezu 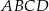 jest równe jest równe 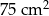 . . | P | F |
Poparcie społeczne dla partii „Zielone żabki” w marcu było równe 25%, a w kwietniu 20%. Zatem poparcie w kwietniu zmalało w porównaniu z marcem o:
A) 5% B) 15% C) 20% D) 25%
Poparcie społeczne dla partii „Radosna przyszłość” w marcu było równe 20%, a w kwietniu 15%. Zatem poparcie w kwietniu zmalało w porównaniu z marcem o:
A) 5% B) 15% C) 20% D) 25%
Poparcie dla partii "WESELI" w marcu było równe 24%. W kwietniu poparcie dla tej partii wynosiło 27%. Zatem poparcie dla partii "WESELI" wzrosło o
A) 3% B) 12,5% C) 25% D) 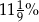
Poparcie społeczne dla partii „Radość i słońce” w marcu było równe 15%, a w kwietniu 12%. Zatem poparcie w kwietniu zmalało w porównaniu z marcem o:
A) 20% B) 6% C) 3% D) 25%
Poparcie dla partii "WESELI" w marcu było równe 40%. W kwietniu poparcie dla tej partii wynosiło 34%. Zatem poparcie dla partii "WESELI" zmalało o
A) 6% B) 12,5% C) 15% D) 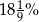
Poparcie dla partii "WESELI" w marcu było równe 24%. W kwietniu poparcie dla tej partii wynosiło 30%. Zatem poparcie dla partii "WESELI" wzrosło o
A) 3% B) 12,5% C) 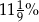 D) 25%
D) 25%
Przedstawiony na rysunku trójkąt 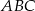 jest prostokątny, ale nie jest równoramienny. Odcinek
jest prostokątny, ale nie jest równoramienny. Odcinek 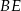 jest wysokością w trójkącie
jest wysokością w trójkącie 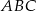 , a półprosta
, a półprosta 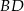 jest dwusieczną kąta prostego.
jest dwusieczną kąta prostego.
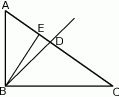
Zaznacz P, jeśli zdanie jest prawdziwe, lub zaznacz F – jeśli jest fałszywe.
Półprosta 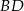 jest dwusieczną kąta jest dwusieczną kąta 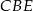 . . | P | F |
Odcinek 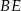 jest wysokością w trójkącie jest wysokością w trójkącie 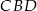 . . | P | F |
Punkt 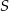 jest środkiem okręgu wpisanego w trójkąt równoramienny
jest środkiem okręgu wpisanego w trójkąt równoramienny 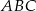 (
(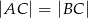 ).
).
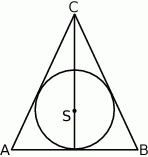
Zaznacz P, jeśli zdanie jest prawdziwe, lub zaznacz F – jeśli jest fałszywe.
Prosta 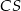 zawiera środkową trójkąta zawiera środkową trójkąta 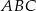 . . | P | F |
Prosta 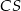 jest symetralną odcinka jest symetralną odcinka 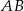 | P | F |
Z okazji Światowego Dnia Książki uczniowie klasy VII zorganizowali quiz wiedzy o postaciach literackich. Quiz można było zakończyć na jednym z poziomów, które zaliczało się kolejno od I do VI. Na diagramie przedstawiono, ile procent uczniów zakończyło quiz na danym poziomie. Na poziomach niższych niż Asia quiz zakończyło dokładnie 32% uczniów biorących w nim udział.
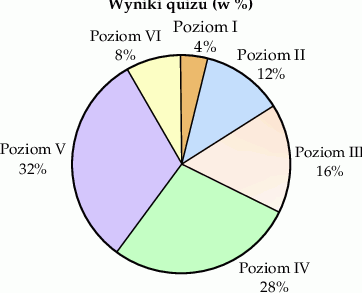
Ile procent uczniów zakończyło ten quiz na poziomach wyższych niż Asia?
A) 40% B) 32% C) 28% D) 8%
Z okazji Międzynarodowego Dnia Liczby 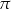 zorganizowano konkurs matematyczny w jednej ze szkół podstawowych. Każdy z uczestników konkursu zajmował jedno z miejsc numerowanych kolejno od I do VI. Na diagramie przedstawiono, ile procent uczniów zakończyło konkurs na danym miejscu. Wiadomo, że 49% uczniów zajęło miejsce o numerze wyższym niż Amelia.
zorganizowano konkurs matematyczny w jednej ze szkół podstawowych. Każdy z uczestników konkursu zajmował jedno z miejsc numerowanych kolejno od I do VI. Na diagramie przedstawiono, ile procent uczniów zakończyło konkurs na danym miejscu. Wiadomo, że 49% uczniów zajęło miejsce o numerze wyższym niż Amelia.
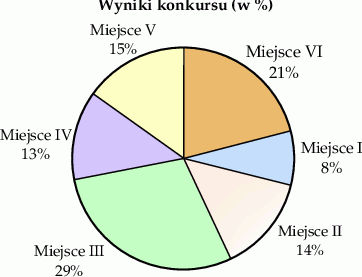
Ile procent uczniów zakończyło konkurs na miejscach o numerach niższych niż Amelia?
A) 8% B) 22% C) 51% D) 36%
Na którym rysunku przedstawiono wykres funkcji 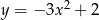 ?
?
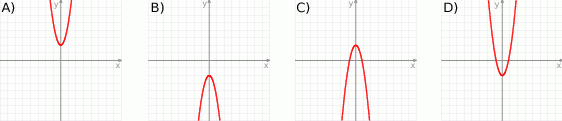
Na którym rysunku przedstawiono wykres funkcji 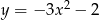 ?
?
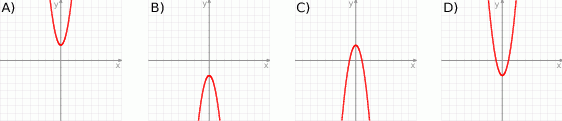
Na którym rysunku przedstawiono wykres funkcji 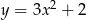 ?
?
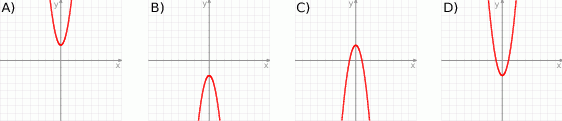
Jeden bok kwadratu o polu 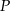 zmniejszono o 30% a drugi zwiększono o 30%. Pole powstałego w ten sposób prostokąta jest równe
zmniejszono o 30% a drugi zwiększono o 30%. Pole powstałego w ten sposób prostokąta jest równe
A) 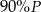 B)
B) 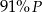 C)
C) 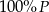 D)
D) 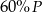
Jeden bok kwadratu wydłużono o 10%, a drugi bok skrócono o 10% w taki sposób, że otrzymano prostokąt. Pole tego prostokąta jest
A) równe polu kwadratu
B) mniejsze od pola kwadratu o 10%
C) większe od pola kwadratu o 10%
D) mniejsze od pola kwadratu o 1%
Dane są liczby  i
i 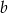 takie, że
takie, że 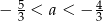 oraz
oraz 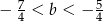 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Iloraz 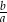 jest zawsze dodatni. jest zawsze dodatni. | P | F |
Różnica 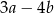 jest zawsze dodatnia. jest zawsze dodatnia. | P | F |
W układzie współrzędnych narysowano sześciokąt foremny o boku 2 tak, że jednym z jego wierzchołków jest punkt 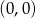 , a jeden z jego boków leży na osi
, a jeden z jego boków leży na osi  . Do tego sześciokąta dorysowujemy kolejne takie same sześciokąty. Umieszczamy je tak, jak na rysunku, aby każdy następny sześciokąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego sześciokąta leżał na osi
. Do tego sześciokąta dorysowujemy kolejne takie same sześciokąty. Umieszczamy je tak, jak na rysunku, aby każdy następny sześciokąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego sześciokąta leżał na osi  . Poniżej przedstawiono dorysowane, zgodnie z tą regułą, sześciokąty, które ponumerowano kolejnymi liczbami naturalnymi.
. Poniżej przedstawiono dorysowane, zgodnie z tą regułą, sześciokąty, które ponumerowano kolejnymi liczbami naturalnymi.
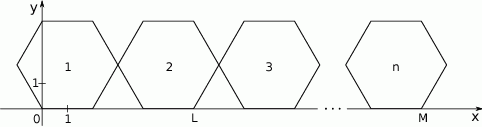
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pierwsza współrzędna wierzchołka 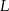 w drugim sześciokącie jest równa 6. w drugim sześciokącie jest równa 6. | P | F |
Pierwsza współrzędna wierzchołka 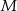 w w  –tym sześciokącie jest równa –tym sześciokącie jest równa 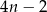 . . | P | F |
W układzie współrzędnych narysowano trójkąt równoboczny tak, że jednym z jego wierzchołków jest punkt 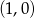 , jeden z wierzchołków jest na osi
, jeden z wierzchołków jest na osi 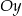 , a jeden z jego boków jest równoległy do osi
, a jeden z jego boków jest równoległy do osi 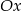 . Do tego trójkąta dorysowujemy kolejne takie same trójkąty. Umieszczamy je tak, jak na rysunku, aby każdy następny trójkąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego trójkąta był równoległy do osi
. Do tego trójkąta dorysowujemy kolejne takie same trójkąty. Umieszczamy je tak, jak na rysunku, aby każdy następny trójkąt miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jeden bok każdego trójkąta był równoległy do osi 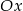 . Poniżej przedstawiono dorysowane, zgodnie z tą regułą, trójkąty, które ponumerowano kolejnymi liczbami naturalnymi.
. Poniżej przedstawiono dorysowane, zgodnie z tą regułą, trójkąty, które ponumerowano kolejnymi liczbami naturalnymi.
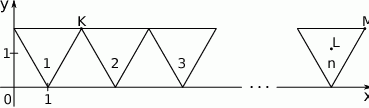
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Środek 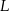 w w  –tym trójkącie ma współrzędne –tym trójkącie ma współrzędne 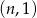 . . | P | F |
Wierzchołek 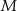 w w  –tym trójkącie ma współrzędne –tym trójkącie ma współrzędne 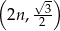 . . | P | F |
W układzie współrzędnych narysowano kwadrat o przekątnej długości 4 tak, że jednym z jego wierzchołków jest punkt 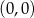 , a jedna z jego przekątnych jest równoległa do osi
, a jedna z jego przekątnych jest równoległa do osi 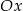 . Do tego kwadratu dorysowujemy kolejne takie same kwadraty. Umieszczamy je tak, jak na rysunku, aby każdy następny kwadrat miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jedna z przekątnych każdego kwadratu była równoległa do osi
. Do tego kwadratu dorysowujemy kolejne takie same kwadraty. Umieszczamy je tak, jak na rysunku, aby każdy następny kwadrat miał z poprzednim dokładnie jeden wspólny wierzchołek oraz by jedna z przekątnych każdego kwadratu była równoległa do osi 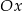 . Poniżej przedstawiono dorysowane, zgodnie z tą regułą, kwadraty, które ponumerowano kolejnymi liczbami naturalnymi.
. Poniżej przedstawiono dorysowane, zgodnie z tą regułą, kwadraty, które ponumerowano kolejnymi liczbami naturalnymi.
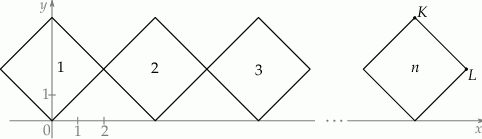
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pierwsza współrzędna wierzchołka 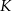 w w  –tym kwadracie jest równa –tym kwadracie jest równa 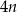 . . | P | F |
Pierwsza współrzędna wierzchołka 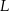 w w  –tym kwadracie jest równa –tym kwadracie jest równa 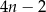 . . | P | F |
O liczbie  wiemy, że
wiemy, że 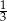 tej liczby jest o
tej liczby jest o  większa od
większa od  tej liczby. Które równanie pozwoli wyznaczyć liczbę
tej liczby. Które równanie pozwoli wyznaczyć liczbę  ?
?
A) 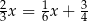 B)
B) 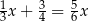 C)
C) 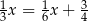 D)
D) 
O liczbie  wiemy, że
wiemy, że 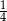 tej liczby jest o
tej liczby jest o  mniejsza od
mniejsza od 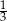 tej liczby. Które równanie pozwoli wyznaczyć liczbę
tej liczby. Które równanie pozwoli wyznaczyć liczbę  ?
?
A) 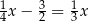 B)
B) 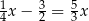 C)
C) 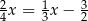 D)
D) 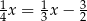
Która z poniższych liczb jest większa od 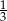 ?
?
A) 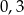 B)
B) 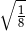 C)
C) 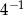 D)
D) 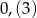
Która z poniższych liczb jest większa od  ?
?
A) 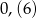 B)
B) 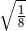 C)
C) 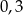 D)
D) 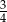
Która z poniższych liczb jest większa od 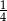 ?
?
A) 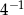 B)
B) 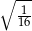 C)
C) 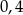 D)
D) 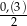
Adam zapisał, w przypadkowej kolejności, podane w programie radiowym wartości temperatury odnotowane pewnego zimowego dnia o godzinie 20:30 w Zakopanem, w Wiśle, w Karpaczu i w Szklarskiej Porębie (zobacz rysunek).
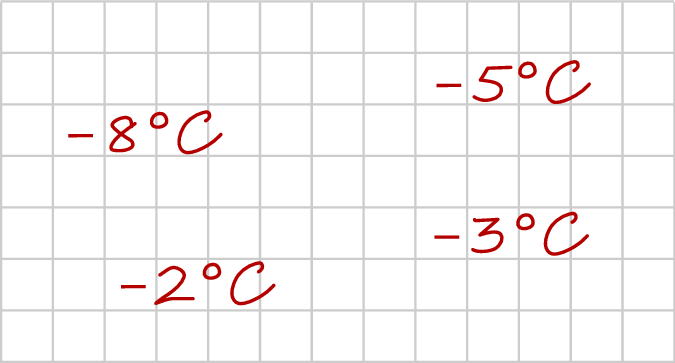
Temperatura w Karpaczu była o 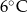 wyższa niż w Szklarskiej Porębie, a w Wiśle była niższa niż w Zakopanem. Temperaturę
wyższa niż w Szklarskiej Porębie, a w Wiśle była niższa niż w Zakopanem. Temperaturę 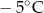 zanotowano w
zanotowano w
A) Szklarskiej Porębie. B) Zakopanem. C) Karpaczu. D) Wiśle.
Rozwiązaniem układu równań 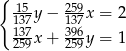 jest para liczb
jest para liczb
A) 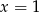 i
i 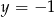 B)
B) 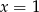 i
i 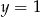 C)
C) 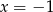 i
i 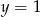 D)
D) 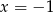 i
i