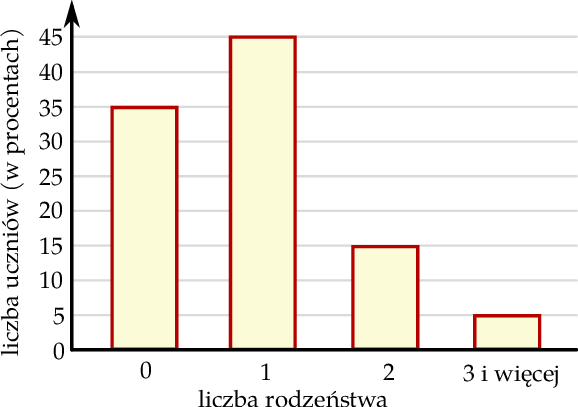
W zagajniku rosną trzy gatunki drzew: buki, brzozy i świerki. Buków jest o 40% więcej niż brzóz i o 15 więcej niż świerków. Świerków jest o 30% więcej niż brzóz. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W tym zagajniku rośnie ponad 200 buków. | P | F |
| Liczba świerków w tym zagajniku jest o 10% mniejsza od liczby buków. | P | F |

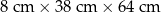
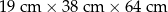
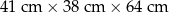
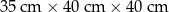
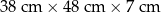
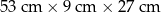
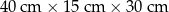
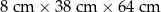
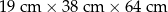
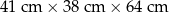
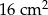
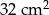
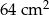
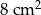
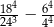 jest równa
jest równa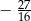
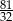
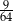
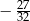
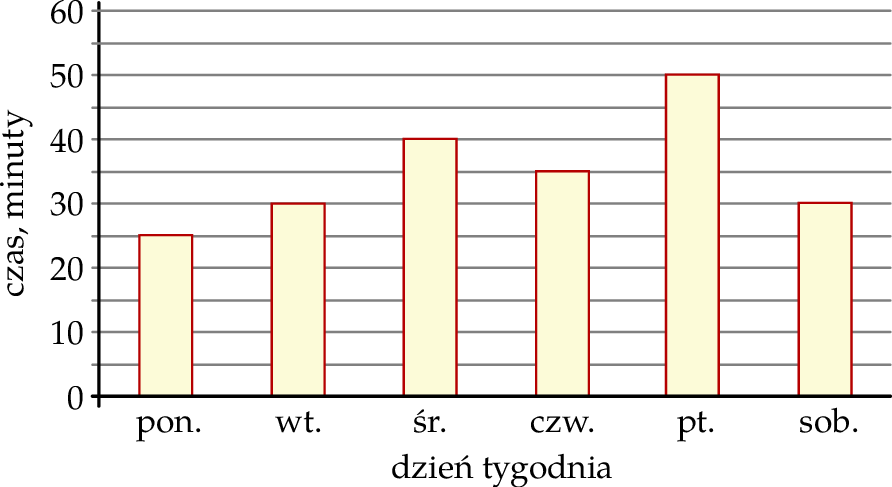
 jest dodatnia, a liczba
jest dodatnia, a liczba 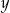 jest ujemna.
jest ujemna. jest dodatnich?
jest dodatnich?  jest ujemna, a liczba
jest ujemna, a liczba  jest dodatnia.
jest dodatnia.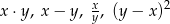 jest ujemnych?
jest ujemnych? 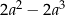 dla
dla 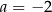 jest równa A/B.
jest równa A/B.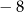
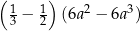 można przekształcić do postaci C/D.
można przekształcić do postaci C/D.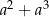
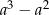


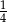
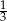
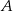 oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia 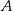 jest równe
jest równe 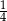
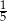
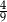
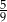


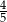

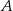 oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że wylosowana z pudełka kula będzie biała. Prawdopodobieństwo zdarzenia 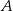 jest równe
jest równe 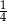
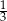
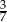

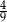

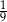
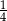
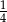
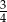
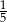

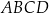 podzielono odcinkiem
podzielono odcinkiem 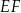 na dwa prostokąty. Odcinek
na dwa prostokąty. Odcinek 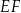 ma długość 11 cm, a odcinek
ma długość 11 cm, a odcinek 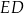 ma długość 2 cm. Pole prostokąta
ma długość 2 cm. Pole prostokąta 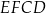 stanowi
stanowi  pola prostokąta
pola prostokąta 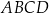 .
. 
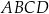 jest równe
jest równe 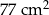 .
.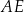 ma długość 7 cm.
ma długość 7 cm. 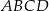 podzielono odcinkiem
podzielono odcinkiem 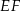 na dwa prostokąty. Odcinek
na dwa prostokąty. Odcinek 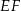 ma długość 12 cm, a odcinek
ma długość 12 cm, a odcinek 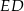 ma długość 2 cm. Pole prostokąta
ma długość 2 cm. Pole prostokąta 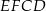 stanowi
stanowi 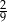 pola prostokąta
pola prostokąta 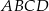 .
. 
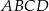 jest równe
jest równe 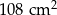 .
.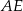 ma długość 7 cm.
ma długość 7 cm. 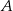 ,
, 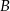 ,
, 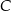 o współrzędnych całkowitych, jak na rysunku.
o współrzędnych całkowitych, jak na rysunku. 
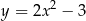 ?
?  ,
, 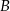 i
i 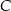 .
. 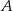 i
i 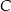 .
. 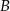 i
i 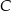 .
. 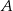 i
i 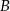 .
. 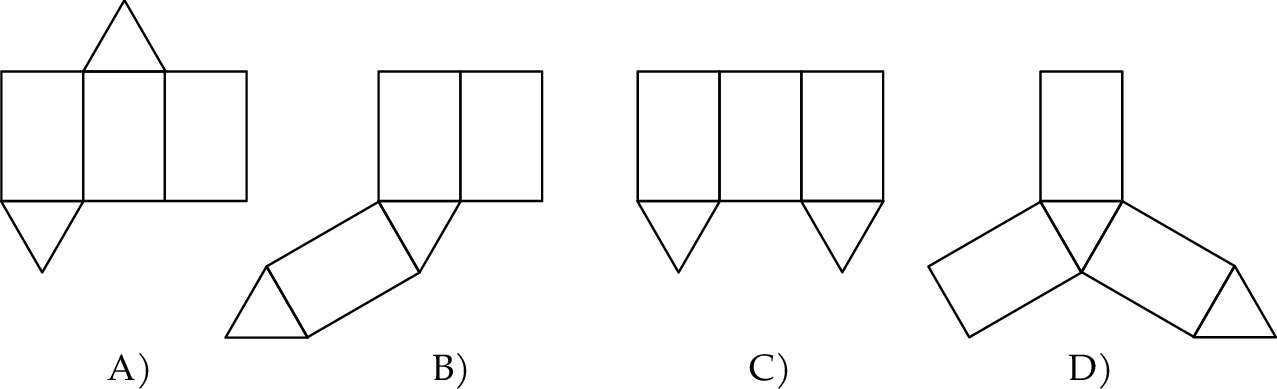
 zbudowany z trzech jednakowych trójkątów prostokątnych o przyprostokątnych długości 3 cm i 4 cm.
zbudowany z trzech jednakowych trójkątów prostokątnych o przyprostokątnych długości 3 cm i 4 cm. 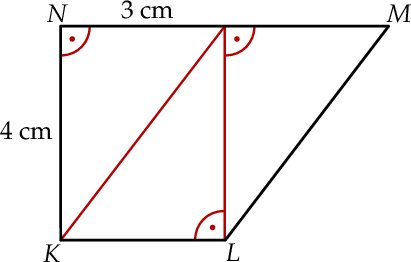
 jest równe
jest równe 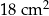 .
.  jest równy 18 cm.
jest równy 18 cm. zbudowany z trzech jednakowych trójkątów prostokątnych o przyprostokątnych długości 3 cm i 4 cm.
zbudowany z trzech jednakowych trójkątów prostokątnych o przyprostokątnych długości 3 cm i 4 cm. 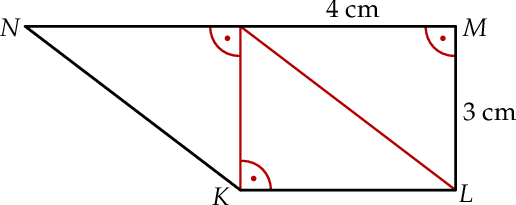
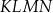 jest równe
jest równe 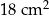 .
. 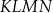 jest równy 18 cm.
jest równy 18 cm.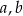 i
i  .
. 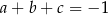 oraz
oraz  jest liczbą mniejszą od
jest liczbą mniejszą od 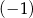 , to suma
, to suma 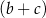 jest A/B.
jest A/B.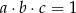 oraz
oraz  jest liczbą większą od zera, to iloczyn
jest liczbą większą od zera, to iloczyn 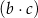 jest C/D.
jest C/D.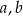 i
i  .
.  oraz
oraz  jest liczbą większą od 1, to suma
jest liczbą większą od 1, to suma 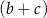 jest A/B.
jest A/B.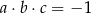 oraz
oraz  jest liczbą większą od zera, to iloczyn
jest liczbą większą od zera, to iloczyn 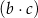 jest C/D.
jest C/D.