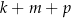Dany jest wzór: 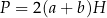 opisujący pole powierzchni bocznej graniastosłupa prostego czworokątnego o wysokości
opisujący pole powierzchni bocznej graniastosłupa prostego czworokątnego o wysokości 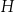 i krawędziach podstawy równych:
i krawędziach podstawy równych: 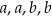 . Którym równaniem opisano
. Którym równaniem opisano 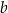 wyznaczone poprawnie z tego wzoru?
wyznaczone poprawnie z tego wzoru?
A) 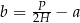 B)
B) 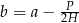 C)
C) 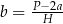 D)
D) 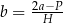
/Szkoła podstawowa/Zadania testowe
Dany jest wzór na pole powierzchni trapezu:
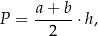
gdzie: 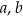 – długości podstaw trapezu,
– długości podstaw trapezu, 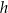 – wysokość trapezu. Długość podstawy
– wysokość trapezu. Długość podstawy  wyznaczona poprawnie z powyższego wzoru opisano równaniem
wyznaczona poprawnie z powyższego wzoru opisano równaniem
A) 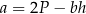 B)
B) 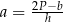 C)
C) 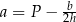 D)
D) 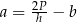
Półkole o promieniu 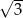 cm zwinięto w stożek.
cm zwinięto w stożek.
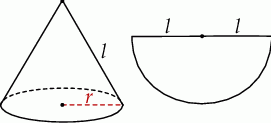
Wysokość tego stożka jest równa
A) 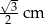 B)
B) 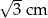 C) 3 cm D) 1,5 cm
C) 3 cm D) 1,5 cm
Na osi liczbowej liczba równa wartości wyrażenia arytmetycznego 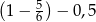 znajduje się między
znajduje się między
A) 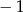 i
i 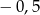 B)
B) 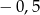 i 0 C) 0 i 0,5 D) 0,5 i 1
i 0 C) 0 i 0,5 D) 0,5 i 1
Na osi liczbowej liczba równa wartości wyrażenia arytmetycznego 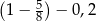 znajduje się między
znajduje się między
A) 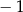 i
i 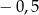 B)
B) 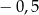 i 0 C) 0 i 0,5 D) 0,5 i 1
i 0 C) 0 i 0,5 D) 0,5 i 1
Pociąg towarowy wyruszył ze stacji 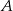 i po 80 minutach dotarł do stacji
i po 80 minutach dotarł do stacji 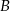 . Na wykresie przedstawiono, jak w trakcie tej podróży zmieniała się odległość pociągu od stacji
. Na wykresie przedstawiono, jak w trakcie tej podróży zmieniała się odległość pociągu od stacji 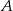 .
.
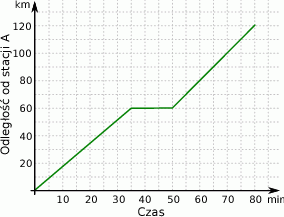
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Pociąg dotarł do połowy trasy po 40 minutach podróży. | P | F |
| Przez pierwsze 30 minut pociąg poruszał się z większą prędkością średnią niż przez ostatnie 30 minut podróży. | P | F |
Pociąg towarowy wyruszył ze stacji 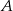 i po 80 minutach dotarł do stacji
i po 80 minutach dotarł do stacji 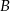 . Na wykresie przedstawiono, jak w trakcie tej podróży zmieniała się odległość pociągu od stacji
. Na wykresie przedstawiono, jak w trakcie tej podróży zmieniała się odległość pociągu od stacji 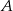 .
.
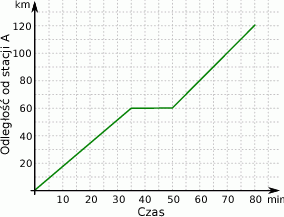
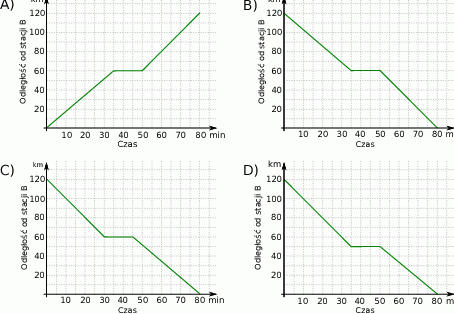
Na którym z poniższych wykresów przedstawiono, jak zmieniała się w trakcie podróży odległość pociągu od stacji
 ?
? 
Na tablicy zaczęto wypisywać kolejne liczby naturalne, które przy dzieleniu przez 4 dają resztę 3.
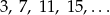
Cyfrą jedności dwusetnej z napisanych liczb jest
A) 3 B) 7 C) 5 D) 9
W ramach prac renowacyjnych odtworzono na ścianie budowli zegar słoneczny, który powstał w 1533 roku. Pod nowym zegarem zapisano datę tej renowacji – MCMXC. Po ilu latach od powstania tego zegara słonecznego odtworzono go na ścianie budowli?
A) Po 457 latach. B) Po 407 latach. C) Po 157 latach. D) Po 107 latach.
Renesansową kamienicę z 1573 roku poddano renowacji w XVIII wieku i umieszczono na niej datę tej renowacji – MDCCXLIX. Po ilu latach od wybudowania dokonano renowacji tej kamienicy?
A) Po 376 latach. B) Po 176 latach. C) Po 396 latach. D) Po 196 latach.
Na starym nagrobku rodzinnym wyryto datę śmierci ojca – MCMXIV oraz datę śmierci jego syna, który zmarł 27 lat później niż ojciec. Którą z dat wyryto na nagrobku jako datę śmierci syna?
A) MCMXLIII B) MCMXXXI C) MCMLI D) MCMXLI
Podatek od dochodów za rok 2016 w Polsce był obliczany według sposobów przedstawionych w poniższej tabeli.
| Podstawa obliczenia podatku | Sposób obliczenia podatku |
| kwota mniejsza lub równa 85 528 zł | 18% podstawy obliczenia podatku pomniejszone o 556,02 zł |
| kwota większa niż 85 528 zł | 14 839,02 zł plus 32% nadwyżki ponad 85 528 zł |
W 2016 roku podstawa obliczenia podatku dla pana Jana wyniosła 84 500 zł. Wysokość podatku (w zł) od dochodu pana Jana opisuje wyrażenie A/B.
A) 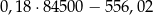 B)
B) 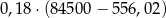
W 2016 roku podstawa obliczenia podatku dla pani Zofii wyniosła 97 300 zł. Wysokość podatku (w zł) od dochodu pani Zofii opisuje wyrażenie C/D.
C) 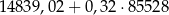 D)
D) 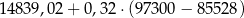
Podatek od dochodów za rok 2016 w Polsce był obliczany według sposobów przedstawionych w poniższej tabeli.
| Podstawa obliczenia podatku | Sposób obliczenia podatku |
| kwota mniejsza lub równa 85 528 zł | 18% podstawy obliczenia podatku pomniejszone o 556,02 zł |
| kwota większa niż 85 528 zł | 14 839,02 zł plus 32% nadwyżki ponad 85 528 zł |
W 2016 roku podstawa obliczenia podatku dla pana Kamila wyniosła 94 500 zł. Wysokość podatku (w zł) od dochodu pana Kamila opisuje wyrażenie A/B.
A) 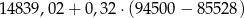 B)
B) 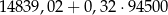
W 2016 roku podstawa obliczenia podatku dla pani Ewy wyniosła 79 300 zł. Wysokość podatku (w zł) od dochodu pani Ewy opisuje wyrażenie C/D.
C) 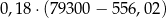 D)
D) 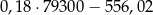
Na przeciwprostokątnej trójkąta prostokątnego o przyprostokątnych długości 1 i 3 zbudowano prostokąt o jednym boku długości 1.
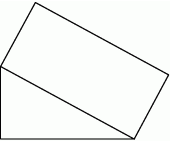
Długość przekątnej tego prostokąta jest równa
A) 3 B) 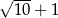 C)
C) 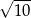 D)
D) 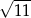
Drut o długości 27 m pocięto na trzy części, których stosunek długości jest równy 2 : 3 : 4. Jaką długość ma najkrótsza z tych części?
A) 4,5 m B) 6 m C) 6,75 m D) 9 m
Linę o długości 100 metrów rozcięto na trzy części, których długości pozostają w stosunku 3 : 4 : 5. Stąd wynika, że najdłuższa z tych części ma długość
A) 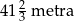 B)
B) 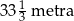 C)
C) 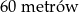 D)
D) 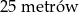
Pręt o długości 40 metrów rozcięto na trzy części, których długości pozostają w stosunku 4 : 5 : 6. Stąd wynika, że najkrótsza z tych części ma długość
A) 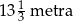 B)
B) 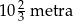 C)
C) 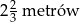 D)
D) 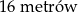
Patyk o długości 96 cm pocięto na trzy części, których stosunek długości jest równy 3 : 4 : 5. Jaką długość ma najkrótsza z tych części?
A) 32 cm B) 27 cm C) 24 cm D) 21 cm
Na rysunku przedstawiono trzy trójkąty.
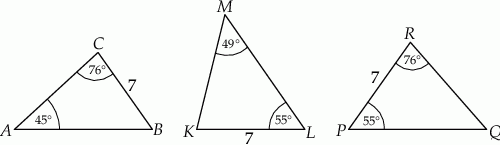
Na podstawie informacji przedstawionych na rysunku można stwierdzić, że
A) trójkąt 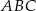 jest przystający do trójkąta
jest przystający do trójkąta 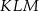 .
.
B) trójkąt 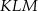 jest przystający do trójkąta
jest przystający do trójkąta 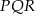 .
.
C) trójkąt 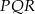 jest przystający do trójkąta
jest przystający do trójkąta 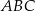 .
.
D) wszystkie trójkąty są do siebie przystające.
Na rysunku przedstawiono trzy trójkąty.
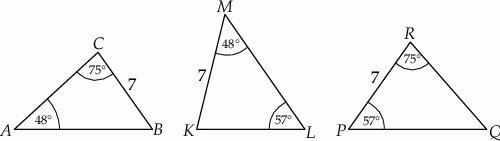
Na podstawie informacji przedstawionych na rysunku można stwierdzić, że
A) trójkąt 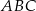 jest przystający do trójkąta
jest przystający do trójkąta 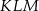 .
.
B) trójkąt 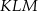 jest przystający do trójkąta
jest przystający do trójkąta 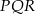 .
.
C) trójkąt 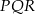 jest przystający do trójkąta
jest przystający do trójkąta 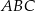 .
.
D) wszystkie trójkąty są do siebie przystające.
Prosta 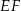 dzieli trapez równoramienny
dzieli trapez równoramienny 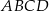 na romb
na romb 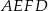 o obwodzie 52 cm i trapez
o obwodzie 52 cm i trapez 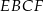 o obwodzie o 13 cm mniejszym od obwodu rombu
o obwodzie o 13 cm mniejszym od obwodu rombu 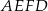 .
.
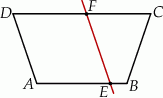
Suma długości odcinków 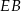 i
i 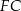 jest równa
jest równa
A) 14 cm B) 13 cm C) 15 cm D) 18 cm
Z sześcianu o objętości 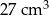 usunięto jedną kostkę sześcienną o krawędzi 1 cm. Ściana usuniętej kostki należała do ściany sześcianu, ale żaden z wierzchołków tej kostki nie należał do krawędzi sześcianu. Pole powierzchni powstałej bryły jest równe
usunięto jedną kostkę sześcienną o krawędzi 1 cm. Ściana usuniętej kostki należała do ściany sześcianu, ale żaden z wierzchołków tej kostki nie należał do krawędzi sześcianu. Pole powierzchni powstałej bryły jest równe
A) 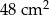 B)
B) 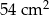 C)
C) 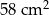 D)
D) 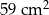
Stosunek długości trzech boków trójkąta jest równy 2 : 4 : 5. Obwód tego trójkąta jest równy 33 cm. Najkrótszy bok tego trójkąta ma długość
A) 2 cm B) 3 cm C) 6 cm D) 11 cm
Pole podstawy walca jest równe 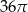 , a pole jego powierzchni bocznej jest 3 razy większe niż pole podstawy. Wysokość tego walca jest równa
, a pole jego powierzchni bocznej jest 3 razy większe niż pole podstawy. Wysokość tego walca jest równa
A) 3 B) 6 C) 9 D) 18
Rozwiązaniem równania 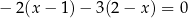 jest liczba
jest liczba
A) 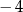 B)
B) 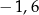 C) 0,8 D) 4 E) 8
C) 0,8 D) 4 E) 8
Rozwiązaniem równania 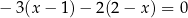 jest liczba
jest liczba
A) 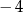 B)
B) 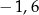 C)
C) 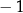 D) 4 E) 8
D) 4 E) 8
Prostokąt podzielono na dwa identyczne trapezy równoramienne i dwa trójkąty w sposób pokazany na rysunku.
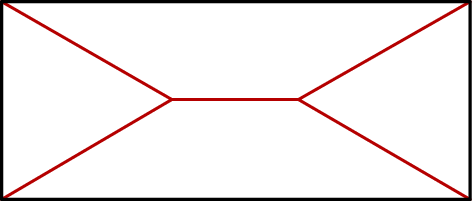
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Trójkąty, które powstały w sposób pokazany na rysunku, sąrównoramienne. | P | F |
Gdyby kąty ostre trapezów miały miarę 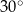 , to powstałe trójkąty byłyby równoboczne. , to powstałe trójkąty byłyby równoboczne. | P | F |
Wykres przedstawia zależność ilości farby pozostałej w pojemniku (w litrach) od powierzchni ściany (w 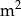 ) pomalowanej farbą z tego pojemnika.
) pomalowanej farbą z tego pojemnika.
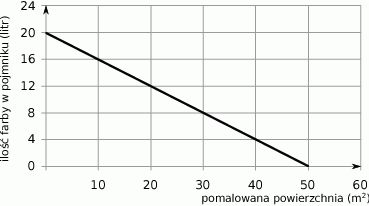
Ile farby pozostało w pojemniku po pomalowaniu 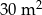 ściany?
ściany?
A) 8 litrów B) 12 litrów C) 16 litrów D) 20 litrów
Wykres przedstawia zależność ilości farby pozostałej w pojemniku (w litrach) od powierzchni ściany (w 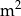 ) pomalowanej farbą z tego pojemnika.
) pomalowanej farbą z tego pojemnika.
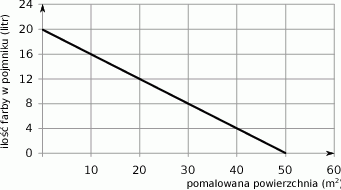
Ile farby zużyto na pomalowanie 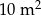 ściany?
ściany?
A) 4 litry B) 8 litrów C) 10 litrów D) 16 litrów
Liczbą przeciwną do liczby 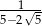 jest liczba:
jest liczba:
A) 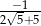 B)
B) 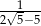 C)
C) 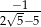 D)
D) 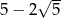
Liczbą przeciwną do liczby 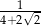 jest liczba
jest liczba
A) 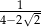 B)
B) 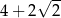 C)
C) 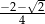 D)
D) 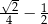
Wartość wyrażenia 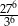 jest równa A/B.
jest równa A/B.
A) 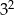 B)
B) 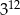
Wartość wyrażenia 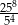 jest równa C/D.
jest równa C/D.
C) 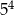 D)
D) 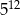
Iloraz 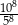 jest równy A/B.
jest równy A/B.
A) 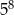 B)
B) 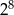
Iloczyn 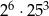 jest równy C/D.
jest równy C/D.
C) 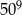 D)
D) 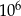
Wartość wyrażenia 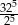 jest równa A/B.
jest równa A/B.
A) 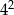 B)
B) 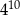
Wartość wyrażenia 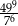 jest równa C/D.
jest równa C/D.
C) 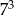 D)
D) 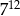
Iloraz 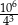 jest równy A/B.
jest równy A/B.
A) 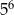 B)
B) 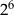
Iloczyn 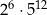 jest równy C/D.
jest równy C/D.
C) 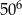 D)
D) 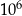
Na osi liczbowej zaznaczono sześć liczb całkowitych. Cztery z tych liczb oznaczono literami: 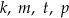 .
.

Które z poniższych wyrażeń ma wartość równą 1?
A) 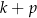 B)
B) 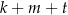 C)
C) 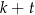 D)
D)